4 로지스틱 회귀분석

4.1 로지스틱 회귀분석이란 무엇인가?

4.1.1 로지스틱 회귀분석이 필요한 이유

사실 통계 공부를 이정도 하다보면, 좀 회의감이 들 수도 있습니다. 꽤 많은 내용을 공부한 것도 같은데 뭐 또 새로운 것을 배워야 하는지. 사실 많은 경우 이 정도 통계를 공부하면 슬슬 자신감도 붙고, 어느 정도 게을러질 만한 이유도 생기고 그렇습니다. 문제는 우리가 지나온 그 길들이 사실은 기초중의 기초였다는 사실이지요. 아니 회귀분석 하나 공부하고 알면 된거 아닌가 싶은데 또 다른 회귀분석이라니 이게 뭔 일인가 싶을 겁니다.

맞습니다. 이래서 통계가 끝이 없는 것이지요.

여기서 우선 말씀드릴 것은 통계적 방법은 지금 이순간에도 새로 만들어지고 세상에 나오고 이론적인 틀이 검증이 되면 누군가는 다시 그걸 소프트웨어에 옮겨서 만들어 시험하고 배포하고 있다는 사실입니다. 왜 이렇게 많은 통계적 방법이 필요할까요?

그 주요한 이유 중의 하나는 바로 통계적 방법론이 가지고 있는 전제조건 때문입니다.

앞에서 공부한 회귀분석은 사실 엄밀하게 따지면 OLS라고 해서 Ordinary Leat Square라는 것입니다. 굳이 우리말로 풀어 쓰자면 일반 최소 제곱 회귀분석 정도로 쓸 수 있겠네요. 그 이름처럼 일반적인 것인데, 문제는 이 일반적인 것이라는게 General이 아니고 Ordinary라는 것입니다. 즉, 아주 정상적이고 매우 합리적인 이상적인 데이터에 사용 가능하다는 것입니다.

이 중에서도 가장 중요한 것이 바로 종속변수입니다. 앞에서 제가 자세하게 설명하지는 않았지만, OLS regression은 전제하고 있는 전제조건이 꽤 많습니다. 궁금하신 분들은 구글링을 하시던가 아니면 책을 찾아 보시길 바랍니다. 이중에서도 가장 예민한 것이 바로 종속변수입니다. OLS에서는 종속변수가 반드시 연속형 변수이어야 합니다. 사실 정확하게 말하자면 연속형 변수이면서도 음의 무한대부터 양의 무한대까지 존재해야하고 종속변수의 값과 값 사이에 무한한게 많은 값이 존재할 수 있어야 합니다. 쉽게말해, 종속변수가 특이한 경우 OLS를 쓸 수 없다는 의미입니다.

로지스틱 회귀분석은 이런 이유로 만들어진 회귀분석입니다.

로지스틱 회귀분석은 종속변수가 이항변수인 경우 사용됩니다. 여기서 이항변수란 쉽게 말해 값이 딱 두 가지 인 경우를 의미합니다. 예를 들자면, 성공/실패, Up/Down, 생존/죽음, Yes/No 이런 경우를 의미합니다. 아마도 어떤 분들은 아니 이런 종속변수라고 하더라도 OLS를 쓰면 안될까? 라는 의문을 가질 수 있습니다. 네, 쓸 수는 있는데 막상 써보면 상당한 문제가 있다는 것을 발견할 수 있습니다. 한번 살펴보겠습니다.

4.1.2 이항변수가 종속변수인 경우 OLS를 적용한 예

샘플예제: 타이타닉 생존 분석
- Download
  - 컴피티션으로 가서 Titanic 검색 후 다운로드
  - 컴피티션의 룰을 수락하도록 함
  - 다운받은 데이터의 압축을 풀어서 사용
  - 파일 중에서 train.csv 를 사용
- Github 다운로드
사용할 변수
- 종속변수: Survived (1: 생존, 0:비생존)
- 독립변수: Pclass (Ticket class)
  - Factor(그룹)변수: 1=1st, 2=2nd, 3=3rd
  - 더미변수 사용: 그룹이 3개이므로 2개의 더미변수 사용 (기준그룹: 1st)

사용할 샘플 데이터는 유명한 타이타닉호의 생존자 데이터입니다. 여기서 우리가 궁금한 것은 타이타닉호 탑승자 중에 누가 생존할 가능성이 더 높았을까? 입니다. 그래서 우리는 종속변수를 생존했는지 (Survived=1), 아니면 생존하지 못했는지 (Survived=0)으로 나눠서 분석에 사용합니다. 인간의 생존은 했는지 못했는지입니다. 저 값이 0.5라면 반만 생존하던지 아니면 반만 생존 못하던지 해야하는데, 여기서 종속변수의 값은 탑승자 개인에 대한 생존여부이므로 0.5라는 값은 생존이라고 하기도 뭐하고 아니라고 하기도 뭐합니다. 벌써 여기서 문제가 발생하기 시작하죠.

더욱이 우리는 위의 모델에서 탑승티켓에 따라서 생존여부가 달랐는지가 궁금합니다. 1등석부터 3등석까지 있는데, 당연히 1등석이 가장 비싸고 3등석이 가장 가격이 쌀 것입니다. 그렇다면 비싼 가격의 표를 산 탑승객이 더 생존 가능성이 높았는지 아닌지 궁금한 것이지요. 만약 1등석의 생존 가능성이 더 높았다면 참으로 억울하면서도 안타까운 일일 것입니다. 그렇다면 이제 이 데이터를 OLS로 분석해 보겠습니다.

우리는 1등석을 기준그룹으로 정했기 때문에, 총 3개의 범주를 가지고 있었으므로 모델에는 2개의 더미변수가 투입되었습니다. 결과분석을 해보면,

1st class의 생존 예측 결과: 0.6296
2nd class의 생존 예측 결과: 0.6296 – 0.1568 = 0.4728
3rd class의 생존 예측 결과: 0.6296 – 0.3873 = 0.2423

이렇게 되고, 셋 다 모두 유의합니다. 이제 이 결과를 어떻게 해석해야 할까요? 우리의 종속변수는 생존(1) 하거나 비생존(0)하거나 밖에 없습니다. 그러나, 위의 예측된 결과는 0도 아니고 1도 아닙니다. 0.5보다 크면 생존이고 0.5보다 작으면 비생존이라고 봐도 될까요? 이게 나쁜 발상은 아니긴 합니다만, 그렇다고 꼭 좋다고 할 수는 없습니다. 왜냐하면, 위의 경우처럼 2등석은 0.4728인데 이러면 생존하지 못한 것인데, 이 결과대로라면 2등석의 승객은 모두 생존하지 못했을까요? 반대로 1등석은 0.6296인데 이 결과대로라면 1등석 승객은 모두 생존한 것일까요? 모두 말이 되지 않습니다.

이와 같이, 이항변수가 종속변수인 경우 OLS를 사용하면 기존의 회귀계수를 해석하는 방법에 문제가 있습니다.

일반적인 OLS는 \(X\)가 1 증가할 때, \(Y\)가 \(\beta\) 만큼 증가한다고 해석합니다
위의 경우는 이러한 해석이 전혀 맞지 않습니다
더불어, 0도 아닌 1도 아닌 예측값의 문제가 여전히 있습니다
심지어, 위에서는 없었지만 경우에 따라 0보다 작은 예측값, 1보다 큰 예측값이 나오기도 합니다

그렇다면, 우리가 기대하는 것은 무엇일까요?

독립변수 \(x\)가 1 증가할 때, 종속변수가 1이 될 확률을 알고 싶습니다
달리말하면, 위의 경우 1등석 승객에 비해 2등석 승객의 생존확률은 \(\beta\)만큼 증가(감소)한다라고 말하고 싶은 것입니다
따라서 이항변수가 종속변수인 경우 OLS는 사용이 불가할 것이라는 생각이 들죠
이러한 이유로 우리는 새로 로지스틱 회귀분석을 배워야 합니다

Youtube 바로 가기

4.2 로짓과 로그오즈비

4.2.1 왜 대부분의 사람들이 로지스틱 회귀분석을 어려워할까?

솔직히 저도 어려웠습니다. 뭐 어찌보면 지금도 어렵습니다. 왜냐하면, 그다지 수리적인 감각이 좋은 편은 아니기도 하고 제가 고등학교에서 문과를 나왔기 때문입니다. 어찌 하다보니, 학부에서는 이과쪽 전공을 하게 되었고, 석박사는 경영쪽을 하긴 했지만 통계쪽에 시간투자를 많이 하다보니 이렇게 되긴 했지만 여전히 통계도 어렵고 로지스틱회귀분석도 어렵습니다.

하지만 제 생각엔 대부분의 경우 로지스틱 회귀분석의 기초를 아무도 알려주지 않기 때문에 어렵다는 생각이 듭니다. 로지스틱이란 말 자체가 어려운데 이걸 어떻게 이해할 수 있겠습니까? 이제 가장 기초부터 하나씩 알아가 보겠습니다.

4.2.2 오즈(Odds)에 대해 알아보자

갑자기 왠 오즈(Odds)인가 싶긴 하겠지만, 앞에서 우리가 보았듯이 우리가 알고 싶은 것은 결국 일종의 확률입니다. 타이타닉의 예에서 본 것 처럼 티켓의 등급에 따라서 생존할 확률이 얼마인지 궁금한 것이지요. 문제는 일반적으로 알고 있는 probability가 아닌 Odds라는 점에서 의아스러울 수 있습니다. 미리 말하자면 이런 경우 일반적인 probability 보다 odds가 더 유리하기 때문에 사용합니다. 일단 Odds에 대해 알아보겠습니다.

오즈(Odds)는 원래 경마장에서 도박 지불률을 정할 때 사용한 것입니다. 만약 Odds를 사용하지 않고 일반적인 probability를 사용할 경우를 살펴보겠습니다.

3마리의 말이 경마 경기에 출전하고 3마리 말의 승리할 확률이 다음과 같을 때,
- A말은 50%의 확률로 승리
- B말은 30%의 확률로 승리
- C말은 20%의 확률로 승리
만약, 참가자에게 1000원에 마권을 사게 하고, 승자를 맞춘 사람에게 3000원씩 지불 한다면,
- A말의 마권을 살 경우 기대값 \(= 3000원 \times 50\% = 1500원\)
- B말의 마권을 살 경우 기대값 \(= 3000원 \times 30\% = 900원\)
- C말의 마권을 살 경우 기대값 \(= 3000원 \times 20\% = 600원\)
그러므로, 바보가 아닌 이상 A말의 마권을 사는 것이 비용 1000원을 초과하는 유일한 선택이 됩니다

만약, 여러분이 주인 입장이라면 50%의 확률로 A말이 이기면, 판매된 마권의 개수 \(\times\) 2000원 만큼 손해이고, 50%의 확률로 A말이 지면, 판매된 마권의 개수 \(\times\) 1000원 만큼 이익이됩니다. 그러므로 주인은 망할 수 밖에 없습니다. 따라서 이런 경우 경마 자체가 성립하지 않습니다. 사실 경마장이 존재하려면 어쩔 수 없이 경마장 주인이 돈을 벌어야 하기 때문입니다.

그렇다면 여러분이 경마장 주인이라 생각하고 대안을 생각해 봅시다.

대안 1: 손해를 보지 않기 위해 예상승률의 역수배로 상금을 지불하기로 함

3마리의 말이 경마 경기에 출전하고 3마리 말의 승리할 확률은 위와 동일할 때,
- A말은 50%의 확률로 승리
- B말은 30%의 확률로 승리
- C말은 20%의 확률로 승리
만약, 참가자에게 1000원에 마권을 사게 하고, 예상승률의 역수배로 상금을 지불하면,
- A말의 마권을 살 경우 기대값 \(= 1000원 \times \frac{1}{50\%} \times 50\% = 1000원\)
- B말의 마권을 살 경우 기대값 \(= 1000원 \times \frac{1}{30\%} \times 30\% = 1000원\)
- C말의 마권을 살 경우 기대값 \(= 1000원 \times \frac{1}{20\%} \times 20\% = 1000원\)
어느 쪽에 걸더라도 기대값 상금이 같아져 패자의 손실과 승자의 이익이 상쇄됨

이렇게 되면, 경마장 주인은 돈을 더 벌지도 잃지도 않고 운영비만 들어가서 결국 손해입니다. 가장 큰 문제는 경마에 참여하는 참여자는 아무 말에나 걸어도 되므로 경마에 참가할 의미가 없어집니다. 더불어 어느 말에 걸어도 참여자 역시 누구도 돈을 벌지도 잃지도 않습니다. 완벽한 제로섬게임이 되어 경마장이 장사가 될리가 없습니다.

그럼 다른 대안을 생각해 봅시다.

대안 2: 오즈(Odds)의 역수배로 상금을 지불하기로 함

3마리의 말이 경마 경기에 출전하고 3마리 말의 승리할 확률은 위와 동일할 때,
- A말은 50%의 확률로 승리
- B말은 30%의 확률로 승리
- C말은 20%의 확률로 승리
만약, 참가자에게 1000원에 마권을 사게 하고, 오즈의 역수배로 상금을 지불할 경우,
- 오즈(Odds) = \(\frac{확률}{1-확률}\)을 의미하므로,
- A의 오즈(Odds) = \(\frac{50\%}{1-50\%} = 1\)이므로, A말의 마권을 살 경우 기대값 \(= 1000원 \times 1 \times 50\% = 500원\)
- B의 오즈(Odds) = \(\frac{30\%}{1-30\%} = 0.43\)이므로, A말의 마권을 살 경우 기대값 \(= 1000원 \times \frac{1}{0.43} \times 30\% \approx 700원\)
- C의 오즈(Odds) = \(\frac{20\%}{1-20\%} = 0.25\)이므로, A말의 마권을 살 경우 기대값 \(= 1000원 \times \frac{1}{0.25} \times 20\% = 800원\)

이렇게 되면, 일단 경마장 주인은 어떤 말이 이겨도 돈을 벌 수 있습니다. 더불어 참가자도 어느 말이 이겼는 지에 따라서 차등적으로 돈을 벌게 되므로 도전할 만한 가치가 있는 것이지요. 물론, 당연한 이야기이지만 어떤 참여자도 경마장을 이기지 못합니다. 1000원을 투자해도 1000원 이상 벌지 못하기 때문이지요. 물론 여기서 들게 된 예는 매우 단순한 예제이므로 현실의 경마와는 다르다는 점을 분명히 말씀드립니다. 하지만, Odds의 시작은 경마장이라는 것이지요.

위의 예를 통해 오즈(Odds)가 무엇인지는 이해가 되시지요?

4.2.3 오즈(Odds)와 일반적인 확률은 다르지 않을까?

그렇습니다. 이런 질문을 할 수 있죠. 우리가 아는 일반적인 확률값 쉽게 말해 p값을 안쓰고 왜 이런 복잡한 것을 쓸까? 그리고 이 오즈(Odds)는 p값을 왜곡하는 것은 아닐까? 결론부터 말하자면 전혀 그렇지 않습니다. 이제 하나의 예제를 보겠습니다.

다음은 어떤 희귀질병의 발병 여부를 도심지역과 비도심지역으로 나누어 본 것입니다.

Table 4.1: 희귀질병의 발병 조사표

	발병 Yes	발병 No	합계
도심지역	1명	1,999명	2,000명
비도심지역	1명	7,999명	8,000명
합 계	2명	9,998명	10,000명

Table 4.1 에서 보면, 도심지역이나 비도심지역이나 모두 1명의 희귀질환자가 발병했지만, 전체 인구수가 꽤 차이가 납니다. 이제 우리는 도심지역과 비도심지역의 오즈(Odds)를 각각 구한 뒤에 이를 나누어 오즈비(Odds ratio)를 만들겠습니다.

\[\text{도심지역 주민의 발병 오즈(Odds)} = \frac{\frac{1}{2000}}{1-\frac{1}{2000}} = \frac{1}{1999}\]

\[\text{비도심지역 주민의 발병 오즈(Odds)} = \frac{\frac{1}{8000}}{1-\frac{1}{8000}} = \frac{1}{7999}\]

\[\text{비도심지역 대비 도심지역의 발병 오즈비(Odds ratio)} = \frac{\frac{1}{1999}}{\frac{1}{7999}} \approx 4.0015\]

그다지 익숙하지 않은 분들에게는 뭐 이리 복잡하게 계산하는가 싶겠지만, 일단 여기서 우리의 최종 관심사는 오즈비(Odds ratio)입니다. 복잡한 계산은 차치하고 우선 오즈(Odds)와 일반적인 확률값인 p값은 큰 차이가 없다는 것이 중요합니다. Table 4.1 에서 보면, 도심지역의 발병률은 p값의 경우 \(\frac{1}{2000}\)이고 오즈(Odds)는 \(\frac{1}{1999}\)로 거의 똑같습니다. 마찮가지로 비도심지역의 경우 p값은 \(\frac{1}{8000}\)이고 오즈(Odds)는 \(\frac{1}{7999}\)로 사실상 거의 차이가 없다고 할 수 있습니다. 따라서 오즈(Odds)로 계산한다고 해도 엄청나게 차이가 나지 않는다는 점입니다. 이는 비도심지역 대비 도심지역의 희귀질병 발생 비율에서도 동일합니다. 이경우 오즈비(Odds ratio)는 다음과 같습니다.

\[\text{비도심지역 대비 도심지역 발병 오즈비(Odds ratio)} = \frac{\frac{1}{1999}}{\frac{1}{7999}} \approx 4.0015\]

p값을 이용해 계산하면 4가 나오는 것과 비교해보면 거의 같은 수준이라고 볼 수 있습니다. 따라서 오즈(Odds)나 오즈비(Odds ratio)가 확률값을 왜곡하지 않는다는 것은 확실합니다.

4.2.4 로짓(logit) = log(Odds ratio) = log(오즈비)

중요한 것은 오즈(Odds)와 오즈(Odds)를 나눈 값인 오즈비(Odds ratio)가 되면, 다소 복잡해 보이긴 하지만 꽨 유용한 점이 있다는 사실입니다. 특히 이 오즈비(Odds ratio)에 log를 붙이면 활용범위가 넓어집니다.

p를 단순확률로 볼 때, p값의 범위는 \(0 < p < 1\)이 됩니다. 이때, 오즈(Odds)의 분모인 \(1-p\)의 범위는 동일하게 \(0 < 1-p < 1\)가 됩니다.
p가 0에 가까워질 수록 오즈비(Odds ratio)는 0을 향해 접근합니다.
p가 1에 가까워질 수록 오즈비(Odds ratio)는 무한대(\(\infty\))를 향재 접근합니다.
그러므로, 오즈비(Odds ratio)의 범위는 \(0 < 오즈비(Odds ratio) < \infty\)가 되고,
오즈비(Odds ratio)에 log를 붙인 log(Odds ratio)의 범위는 \(-\infty < log(Odds ratio) < \infty\)가 됩니다.
여기서 log(Odds ratio)를 다른 말로 로짓(logit)이라고 부릅니다.

아마도, 저와 같은 문과출신들은 이게 그래서 무슨 뜻이야? 라고 생각하실 것입니다. 특히, 위의 5번이 핵심인데 이해가 잘 안되시거나 고등학교 때 배운 로그가 잘 생각나시지 않는 분을 위해 위의 5번을 좀 더 자세하게 풀어보면 다음과 같습니다.

로짓(logit) = log(Odds ratio) = log(오즈비)
- 종속변수가 0과 1인 이항변수일 때: 오즈비(Odds ratio)를 구하면 최소값은 0이 됩니다
  - 이 값 0에 로그를 취하되 밑수를 네이피어수(e=2.718)로 할 경우 \(\log_e 0\)은 마이너스 무한대가 됩니다
  - 왜냐하면, 2.718의 수를 계속 곱하더라도 2.718보다 작은 수가 되지는 않기 때문입니다
  - 그러나, 여러 차례 계속 나누게 되면 1보다 점점 작은 값이 되어 0을 향해 움직이는데,
  - 나눈다는 것은 마이너스 제곱의 의미이므로 마이너스 무한제곱이 되면 거의 0이 됩니다
  - 그래서 \(\log 0 = −\infty\)가 됩니다
- 종속변수가 0과 1인 이항변수일 때: 오즈비(Odds ratio)를 구하면 최대값은 1이 됩니다
  - 오즈비는 \(\frac{1}{1-1}\)이므로 계산이 불가 하지만 분모를 0에 가까운 0이 아닌 가장 작은 수라 가정하면, 1을 0에 가까운 가장 작은 수로 나누었으므로 무한대가 됩니다
  - 여기에 로그를 취하면 \(\log_e \infty = \infty\)가 되는 것입니다

4.2.5 그래서 뭐 어쩌라고?

여기까지 와서도 이게 도대체 그래서 뭐 어쩌란 말이냐? 라고 물으실 수도 있습니다. 여기서 중요한 것은 앞서 왜 우리가 종속변수가 이항변수일 때, OLS 회귀분석을 사용하지 못하느냐를 다시 떠올려야 합니다. OLS 회귀분석에서 종속변수는 음의 무한대로부터 양의 무한대까지 가능한 연속변수이어야 한다고 했습니다. 위에서 우리가 어렵게 구한 로짓(logit)은 결국 0과 1이라는 이항변수를 음의 무한대에서 양의 무한대까지로 변환하는 일종의 변환방법인 것입니다.

결론적으로, 우리의 종속변수가 이항변수일 때, 이 이항변수를 로짓(logit)으로 변환하면, OLS 회귀분석을 할 수 있다는 의미가 됩니다. 다만, 이렇게되면 기존의 OLS와는 다소 다른 점들이 있으므로 우리는 이제 그런 것들을 공부하면 됩니다.

고생 많으셨습니다.

Youtube 바로 가기

4.3 로지스틱 회귀분석을 해석해보자

앞서 우리는 왜 굳이 로지스틱 회귀분석을 공부해야 하는지 그리고 왜 그렇게 복잡한 과정을 거쳐 로짓(logit)을 구하는지 알아봤습니다. 반복해 보자면 이렇게 오즈비(Odds ratio)에 로그를 취하면 이항변수도 연속형 변수마냥 OLS를 할 수 있다는 것을 알았습니다. 문제는 이렇게 종속변수를 변환하게 되면, 해석이 단순하지 않다는 점이 문제입니다. 사실 대부분의 논문들이 유의하다 유의하지 않다라고 앵무새처럼 반복할 뿐 이를 제대로 해석하는 논문은 생각보다 찾기 힘든 것이 현실입니다. 이번 기회에 로지스틱 회귀분석을 어떻게 해석해야 하는지 제대로 공부해 보도록 합시다.

4.3.1 로지스틱 회귀분석의 예제

우리는 앞서 보았던 타이타닉 생존자 데이터를 샘플로 하여 분석결과를 보고 해석해 보도록 하겠습니다.

샘플예제: 타이타닉 생존 분석
- Github 다운로드
사용할 변수
- 종속변수: Survived (1: 생존, 0:비생존)
- 독립변수
  - Age (나이): 연속형 변수
  - Fare (요금): 배에 탈 때, 낸 비용(아마도 앞서 본 Class와 상관관계가 많을 것임)
  - Gender (성별): 여성을 기준그룹(=0)으로 지정 (남성더미가 될 것임)
  - SibSp (동반자): 여기서 동반자란 형제/자매 혹은 배우자의 숫자
    - 연속형 변수로 사용할 수도 있으나 여기서는 factor 변수로 사용

일단 묻지도 따지지도 말고 결과표부터 보겠습니다. 상단은 OLS 회귀분석이고 하단이 로지스틱 회귀분석 결과입니다.

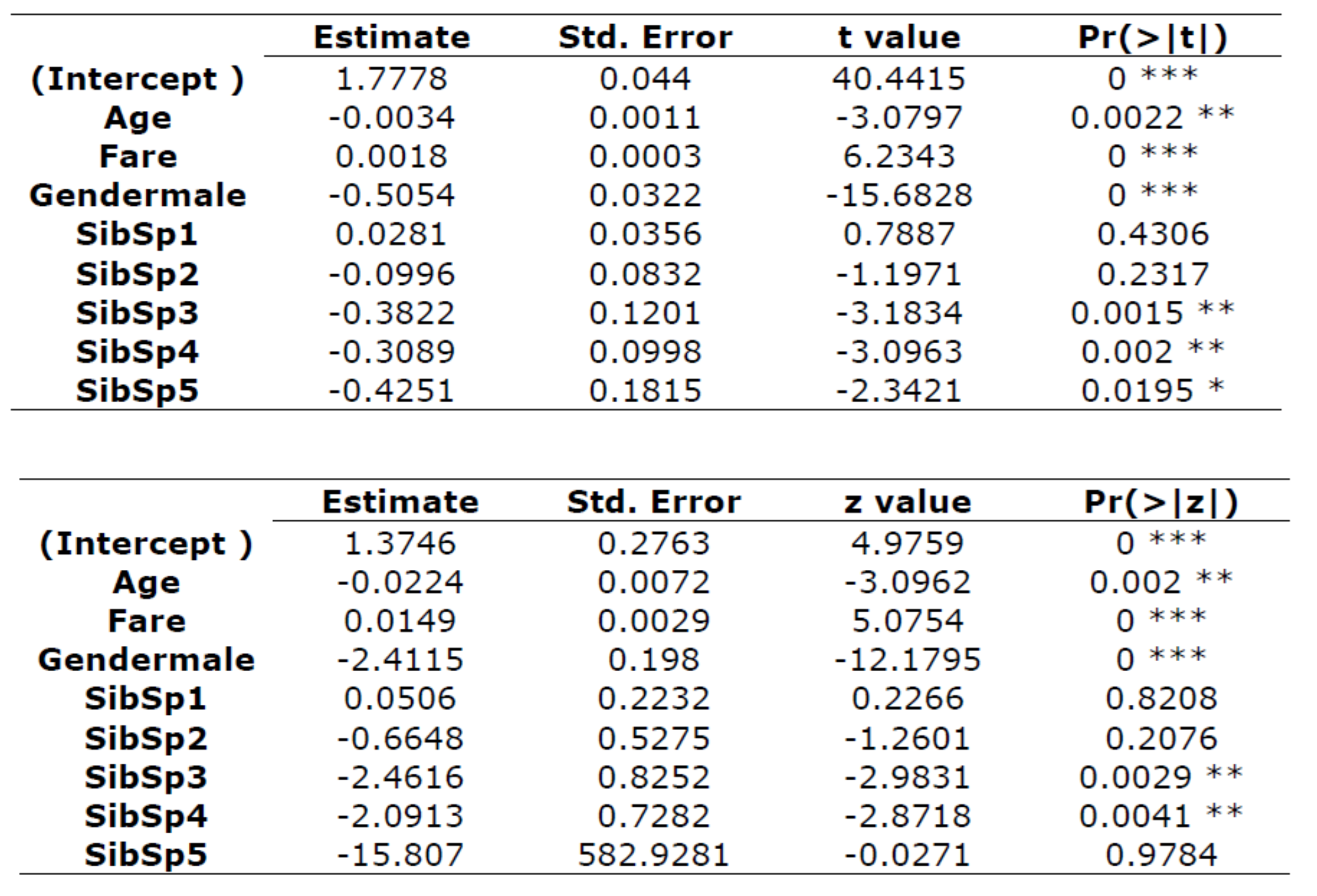
회귀계수의 크기는 좀 다르긴 하지만 전체적으로 유의한지 아닌지는 비슷해 보이긴 합니다. OLS는 우리의 관심사가 아니므로 일단 넘어가 보겠습니다.

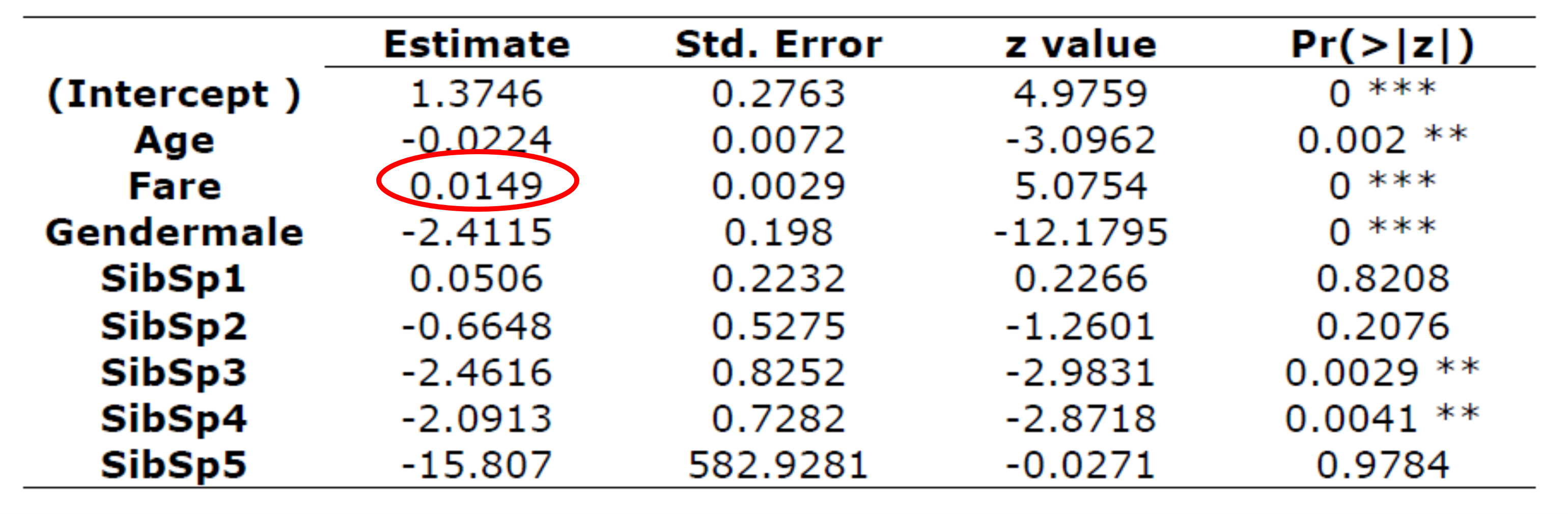
우선 독립변수 Fare를 보겠습니다. p값을 보니 매우 유의합니다. 회귀계수는 0.0149인데 이걸 어떻게 해석하느냐가 문제입니다. 우선 유의할 경우 회귀계수의 +/-를 먼저 살펴보아야 합니다.

회귀계수가 양수(+)이면 생존(Y=1) 가능성이 높은 것
회귀계수가 음수(-)이면 생존(Y=1) 가능성이 낮은 것

그러므로, 위의 Fare의 결과가 의미하는 것은 요금을 많이 낼 수록 생존의 가능성이 높아졌다는 것입니다. 물론 얼마나 높아졌는지는 해석을 해봐야 알 것입니다. 문제는 이 회귀계수 0.0149는 기존의 OLS처럼 해석할 수 없다는 것입니다. OLS의 경우 요금이 1 dollar 높아질 수록 생존확률이 0.0149 높아진다는 식으로 해석하겠지만 여기 종속변수에는 로그가 붙어 있으므로 이런 해석은 불가능합니다.

log를 제거하기 위해서는 exponential을 씁니다. 둘은 마치 곱셈과 나눗셈 마냥 짝을 이룬다고 보시면 됩니다. 이를 수학에서는 이렇게 표현합니다. exp(X)라고 합니다. 따로 계산하려고 하지말고 엑셀을 이용해서 함수 **=exp(#)*]**를 사용하시기 바랍니다. 괄호 안에 # 대신에 숫자를 넣으시면 됩니다. 계산을 해보면,

\[exp(0.0149) = 1.015\]

여기서 1.015는 오즈비(Odds ratio)입니다. 따라서, 해석은 다음과 같이 합니다. 요금이 1 dollar 증가할 수록, 생존 가능성은 1.015배 증가한다 회귀계수가 양수일 경우는 그래도 해석이 무난한 편입니다. 문제는 회귀계수가 음수일 경우가 해석이 쉽지 않다는 점입니다. 이를 확인하기 위해 Figure 4.3 의 Age 변수를 봅시다. Age 변수는 음의 방향으로 유의합니다. 즉, 나이가 많을 수록 생존확률은 낮아진다는 것입니다. 이제 이 음수인 회귀계수에 exponential을 붙여 계산을 해보면,

\[exp(-0.0224) \approx 0.98\]

이게 무슨 뜻일까요? 정확한 해석은 이렇습니다. 나이가 1살 증가할 수록, 생존 가능성은 약 0.98배 증가한다 쉽게 이해가 되지 않으시지요? 주의할 점은 증가한다고 해석을 항상 해야한다는 점입니다. 그러나 실질적으로 1보다 작은 배수로 증가를 한다는 것은 결국 감소한다는 뜻입니다. 따라서 나이가 1살 증가할 수록 생존 가능성이 낮아지는 것은 맞긴한데, 0.98배 증가한다는 것은 도대체 얼마나 감소하는 것인지 헷가릴 수 밖에 없습니다. 다른 예를 하나 더 보겠습니다. SibSp3라는 변수는 더미변수로 동반자가 없는 경우에 비해 동반자가 3명인 경우의 생존확률을 의미합니다. 이 값 역시 마이너스로 유의합니다. 동반자가 1명이나 2명까지는 유의하지 않다가 3명이 되어서야 유의합니다. 의미상으로는 동반자가 3명인 경우 동반자가 없는 경우보다 생존확률이 훨씬 낮다는 의미가 됩니다. 이제 exponential을 붙여 계산해 보도록 합시다.

\[exp(-2.4616) \approx 0.085\]

정확하게 해석해 보자면, 동반자가 없는 경우에 비해 동반자가 3명인 경우, 생존 가능성은 0.085배 증가한다라고 해석합니다. 도통 와 닿지 않는 해석입니다. 그래서 사실 로지스틱 회귀분석은 복잡하더라도 반드시 %로 변환하여 해석하는 것이 보다 좋습니다. 문제는 %로 변환하는 방법이 조금 복잡하다는 것입니다. 이 경우를 %로 변환해 보겠습니다.

\[\{exp(-2.4616) – 1\}×100 = -91.5\]

계산 방법은 exponential을 붙인 값에서 1을 빼고 다시 100을 곱하면 %로 변환됩니다. 위의 결과를 해석하면, 동반자가 없는 경우에 비해 동반자가 3명인 경우, 생존 가능성은 91.5% 감소한다라고 해석합니다. 사실 생존 확률이 91.5%나 감소한다는 것은 정말 엄청난 변화라고 볼 수 있습니다. 아무래도 지켜야할 동반자가 많을 수록 생존확률은 떨어지지만 그 시작이 3명부터라고 보면, 참 슬픈 일이 아닐 수 없습니다. 이는 4인 가족의 경우 생존 확률이 매우 낮다는 의미이기 때문입니다.

그렇다면, 앞에서 봤던 Fare를 %로 변환하여 다시 해석해 봅시다.

\[\{exp(0.0149) – 1\}×100 = 1.5\]

즉, 요금이 1 dollar 증가할 수록, 생존 가능성은 1.5% 증가한다는 것입니다. 사실 이렇게 보면 큰 차이처럼 보이지 않아도 만약 100달러 정도 요금의 차이가 난다면 이는 거의 생존자체를 바꿀 수 있는 차이가 될 수도 있기 때문에 작다고만 할 수는 없을 것 같네요. 그럼 이제 마지막으로 성별에 따른 생존 확률를 보겠습니다.

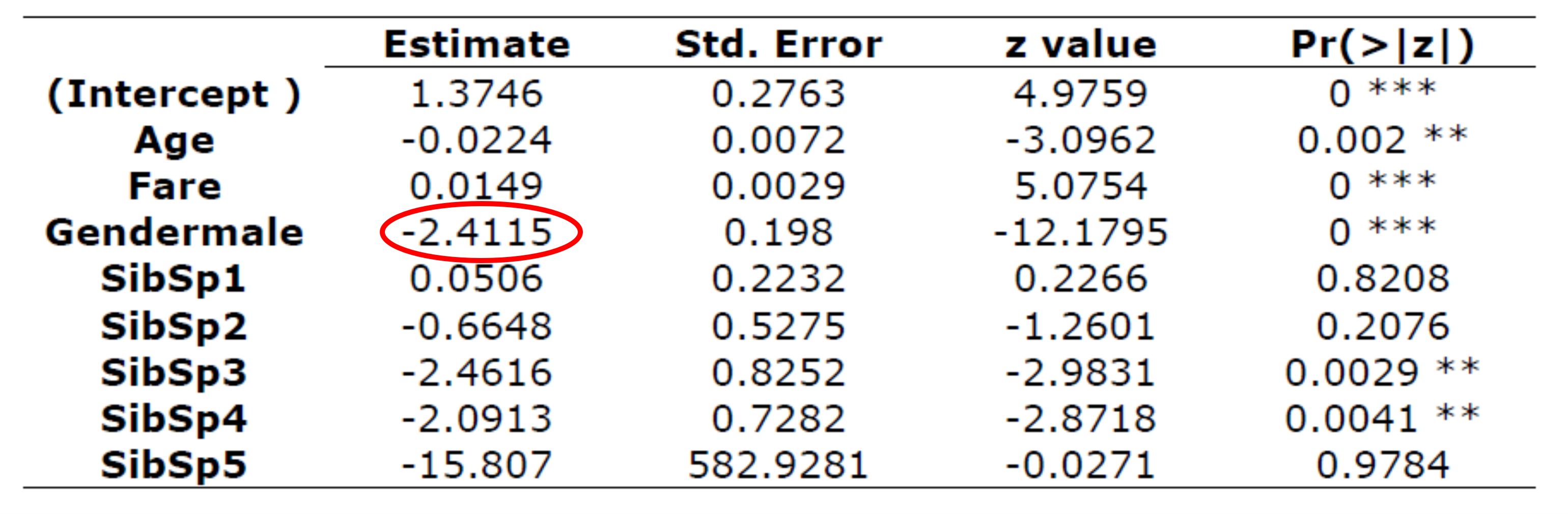
단순하게 exponential만 취하면 \(exp(-2.4115) \approx 0.09\)가 되어, 여성에 비해 남성의 생존률은 0.09배 높다라는 결과가 됩니다. 가끔, 어떤 분들이 이런경우 귀찮으니 그냥 이 결과를 남성에 비해 여성의 생존률이 91% 정도 높다고 해석해도 되지 않나요? 라고 묻는 경우가 있습니다. 문제는 이런식의 해석이 완전히 틀렸다는 것입니다. 특히나, 기준그룹을 바꿔서 해석할 때는 정말 주의해야 합니다. 이 경우는 사실 0에서 1로 증가하는 것을 반대로 1에서 0으로 감소하는 것을 전제로 하는 해석입니다. 이게 잘 이해가 안되실 수도 있는데 일반 OLS에서는 독립변수 1의 증가나 1의 감소가 사실상 같은 의미가 됩니다. 그래서 OLS에서는 독립변수가 1 증가할 때, 종속변수가 회귀계수(\(\beta\))만큼 증가한다고 해석합니다. 이 결과를 바꿔도 사실 동일합니다. OLS에서는 독립변수가 1 감소할 때, 종속변수가 회귀계수(\(\beta\))만큼 감소한다라고 해석해도 아무 문제가 없습니다. 그러나 로지스틱 회귀분석에서는 독립변수의 감소는 회귀계수에 마이너스(-)를 붙여서 해석하는 방식으로 되어서는 안됩니다. 위의 경우 성별은 더미변수이므로, 0인 여성을 기준으로 1인 남성에 대한 회귀계수입니다. 따라서 해석도 여성대비 남성이 이러이러하다 라는식으로 해석해야 합니다. 그런데 위의 경우 만약 남성대비 여성이 이러이러하다고 해석하고자 한다면 이는 독립변수의 증가가 아닌 독립변수의 감소로 해석을 하는 것입니다.

이제 %로 변환하여 제대로 계산해 봅시다. 이 경우 \(exp(-2.4115) \approx 0.09\)이었기 때문에, 기준그룹을 바꿔서 해석하고자 한다면, 0.09가 아닌 \(\frac{1}{0.09}\)을 넣고 계산해야 합니다. 이점이 가장 다른 부분입니다.

\[\{\frac{1}{0.09} – 1\} ×100 \approx 1011\]

상상할 수도 없는 엄청난 숫자가 나오네요. 해석하자면, 남성에 비해 여성의 생존률은 1011% 높다라고 해석해야 합니다. 놀랍습니다.

정리해 보자면, 로지스틱 회귀분석 결과 해석할 때는,

exp(회귀계수)는 오즈비(odds ratio)로 해석한다
{exp(회귀계수) – 1} × 100 은 % 증가 또는 감소로 해석 가능하다
독립변수가 1단위 증가할때와 1단위 감소할때의 해석은 다르다
- \(\{\frac{1}{exp(\text{회귀계수})} – 1\} \times 100\) 으로 계산해서 해석해야 한다
모든 독립변수의 증감에 대하여 종속변수가 1(Y=1)이 되는 확률로 해석한다

로지스틱 회귀분석은 종속변수가 이항변수임에도 마치 OLS처럼 회귀분석을 할 수 있도록 해주는 매우 좋은 방법입니다. 하지만 해석이 까다롭고 조심스럽기 때문에 해석을 잘 하는 것이 무엇보다 중요합니다.

Youtube 바로 가기

4.4 로지스틱 회귀분석을 실습해보자

실습데이터는 계속 보아왔던 타이타닉 생존자 데이터를 이용하도록 하겠습니다.

샘플예제: 타이타닉 생존 분석
- Github 다운로드
사용할 변수
- 종속변수: Survived (1: 생존, 0:비생존)
- 독립변수
  - Age (나이): 연속형 변수
  - Fare (요금): 배에 탈 때, 낸 비용(아마도 앞서 본 Class와 상관관계가 많을 것임)
  - Gender (성별): 여성을 기준그룹(=0)으로 지정 (남성더미가 될 것임)
  - SibSp (동반자): 여기서 동반자란 형제/자매 혹은 배우자의 숫자
    - 연속형 변수로 사용할 수도 있으나 여기서는 factor 변수로 사용

Youtube 바로 가기