1 카이제곱(\(\chi^2\)) 검정
1.1 카이제곱(\(\chi^2\)) 검정에 대해 알아보자
1.1.1 지금까지와 다른 것
지금까지 우리는 t-test, 분산분석(ANOVA)를 중심으로 공부해 왔습니다. 공통점이 있다면 종속변수는 연속변수(Continuous) 즉 양적변수(Quantitative)이고, 독립변수는 사실상 질적변수(Qualitative)였다는 점입니다. 즉, 독립변수는 2 개 혹은 3 개의 그룹이었고 종속변수만 연속변수였습니다. 그런데, 만약 독립변수와 종속변수 둘 다 명목척도 혹은 질적변수(Qualitative)라면 어떻게 될까요? 지금까지 배운 것으로 분석이 가능할까요?
그렇지 않습니다. 독립변수와 종속변수가 모두 질적변수일 경우 사용하는 방법이 바로 교차분석입니다. 영어로는 chi-square(\(\chi^2\)) test라고 합니다. 앞서 우리가 보았던 t-test 혹은 분산분석의 F-test를 떠 올려본다면, 당연히 여기서는 \(\chi^2 \; \text{value}\)와 \(\chi^2\)분포가 있습니다. 이제 하나씩 알아보겠습니다.
1.1.2 카이제곱(\(\chi^2\)) 검정의 목적
우선 카이제곱(\(\chi^2\)) 검정은 언제하는 것일까요? 앞에서 이야기 한 것처럼 독립변수와 종속변수가 모두 명목척도 즉 질적변수인 경우입니다. 결론적으로 데이터는 사실상 개수(count)가 됩니다. 앞에서 공부한 t-test나 분산분석(ANOVA)의 목적은 둘 혹은 세 그룹의 평균값이 같은지 다른지 알고 싶을 때 하는 것이었습니다. 카이제곱(\(\chi^2\)) 검정의 목적은 다소 달라집니다. 카이제곱(\(\chi^2\)) 검정은 변수가 한 개인 경우에도 할 수 있는데, 변수의 그룹간 비율이 같은지 다른지 확인할 대 가능합니다. 만약 한 변수의 그룹이 2 개라면 카이제곱(\(\chi^2\)) 검정보다 단순한 Binomial test라는 것을 합니다. 그룹이 3 개 이상인 경우에는 카이제곱(\(\chi^2\)) 검정을 하게 됩니다. 또한 카이제곱(\(\chi^2\)) 검정은 변수가 두 개인 경우에도 할 수 있는데, 두 변수 사이의 연관성(Association)을 보고자 할 때 카이제곱(\(\chi^2\)) 검정을 사용합니다. 예를 들어 휴대폰 사용과 암의 발병율을 조사할 때 가능합니다.
1.1.3 카이제곱(\(\chi^2\)) 계산식
\[\chi^2 \; \text{value} = \Sigma \frac{(O - E)^2}{E}, \; \text{df} = \text{범주의 개수} - 1\]
위의 식에서 O는 관찰빈도(Observed frequency), E는 기대빈도(Expected frequency)입니다. 위의 식에서 관찰빈도는 데이터에서 자연스럽게 주어지는 값이 되고, 기대빈도는 별도의 방법을 이용해 구해야 합니다. 여기서 말하는 기대빈도란 개념적으로 설명하자면 어떤 특별한 이유가 없는한 이렇게 동일하게 나와야 한다는 일종의 기대수치와 같은 개념입니다. 에를 들어 고객 데이터에서 특별한 이유가 없는 한 남성고객과 여성고객의 빈도는 동일하게 나타나야 할 것이라고 가정하면, 총 1000명의 고객이 있을 경우 남성과 여성은 각각 500명씩 있어야 한다는 식의 개념이 바로 기대빈도입니다.
그럼 이제 조금 더 자세하게 알아보도록 하겠습니다.
1.2 일원 카이제곱(One-way \(\chi^2\) test) 검정을 계산해 보자
여기서 일원(one-way)는 변수가 1 개라는 의미입니다. 한 개의 변수가 당연히 명목척도/질적변수이어야 합니다. 당연히 이 명목척도는 2 개 이상의 범주를 가지고 있어야 하며 데이터 코딩을 할 때는 한 개의 변수이므로 하나의 열(column)에 넣어야 합니다. 다음과 같은 예를 들 수 있습니다.
- Payment method라는 변수는 총 4개의 범주로 구성(Bank transfer/Credit card/Electronic check/Mailed check)
- 고객의 지불방법에 따라 고객의 수가 차이가 나는지 알고 싶다면 일원 카이제곱(One-way \(\chi^2\) test) 검정을 시행
데이터는 다음과 같습니다.
| Level | Count (빈도) | % |
|---|---|---|
| Bank transfer | 1544 | 21.90% |
| Credit card | 1522 | 21.60% |
| Electronic check | 2365 | 33.60% |
| Mailed check | 1612 | 22.90% |
| Total (계) | 7043 | 100.00% |
우리가 앞서 분산분석(ANOVA)에서 사용했던 데이터 중에서 독립변수입니다. 총 4 개의 범주가 있고 각 범주는 Bank transfer 21.9%, Credit card 21.6%, Electronic check 33.6%, Mailed check 22.9%로 구성되어 있습니다. Table 1.1 에서 그냥 빈도라고 되어 있는 것이 카이제곱 검정에서는 관찰빈도(O)가 됩니다. 이제 기대빈도까지 계산한 표를 확인해 보겠습니다.
| Level | 관찰빈도(O) | % | 기대빈도(E) | (O – E)2÷E |
|---|---|---|---|---|
| Bank transfer | 1544 | 21.90% | 1761 | 26.74 |
| Credit card | 1522 | 21.60% | 1761 | 32.44 |
| Electronic check | 2365 | 33.60% | 1761 | 207.16 |
| Mailed check | 1612 | 22.90% | 1761 | 12.61 |
| Total (계) | 7043 | 100.00% | 278.95 |
기대빈도는 총 7043개의 데이터가 4 개의 범주에 동일한 비율로 분포되어 있을 것이라는 가정에 따라서 \(7043 \div 4 = 1760.75\)가 되어 반올림하여 기대빈도는 각 1761로 정하였습니다. 이제 관찰빈도(O)와 기대빈도(E)를 사용하여 각 범주의 계산 값을 구해보면 위의 Table 1.2 의 마지막 열(column)에 정리되어 있습니다.
이제 \(\chi^2 \; \text{value} = 26.74 + 32.44 + 207.16 +12.61 = 278.95\)가 됩니다. 이 경우 범주의 개수가 4 개이므로 \(df = 4 - 1 = 3\)이 됩니다. 이 두 가지를 표기하는 방법은 다음과 같습니다.
\[\chi^2_{df=3} = 278.95\]
이때의 p-value를 구하려면 엑셀에서 chidist라는 함수를 사용하면 됩니다. 실제로 구해보면 거의 0에 가까운 값이 나와 매우 유의하다는 결과가 나옵니다. 카이제곱 검정 결과가 유의하다는 것은 무슨 뜻일까요?
이를 이해하려면 카이제곱 검정의 통계적 가설을 이해할 필요가 있습니다. 우리가 테스트한 내용을 통계적 가설로 쓰면 다음과 같습니다.
\[H_0: \text{P(Bank transfer)} = \text{P(Credit card)} = \text{P(Electronic check)} = \text{P(Mailed check)}\] \[H_a: \text{Proportion of 4 categories are not even}\]
귀무가설에서 P는 영어의 Proportion 즉 비율을 의미합니다. 여담입니다만, 가끔 ratio와 proportion이 뭐가 다르냐는 질문을 받습니다. 둘 다 한 개의 값을 다른 값으로 나눈 것이라는 계산 방식은 비슷합니다만, 일반적으로 ratio는 완전히 서로 다른 개념의 것을 나누어 비율로 표현한 것이라면, Proportion은 전체 중 특정한 부분이 차지하는 비율을 의미한다고 볼 수 있겟습니다. 즉, 여기서 네 개의 Proportion을 합치면 1이 되는 경우이므로 이런 경우에는 Proportion이라고 부릅니다.
그러므로 카이제곱 검정이 유의하다는 것은 비율이 각 범주 간에 동일하지 않다는 의미가 되는 것입니다. 사실 여기서 이야기 하는 유의하다는 것은 기대되는 비율 즉 모든 범주가 동일할 것이라는 기대에 다르다는 의미가 됩니다.
그러나 만약 기대빈도가 이론에 의해 사전적으로 1:1:1:1이 아니고 1:1:2:1이라면 기대빈도 자체가 애초에 다르게 설정되어 카이제곱 값이 계산되어야 합니다. 이 경우 20%:20%:40%:20%로 계산되어야 해서 1049:1049:2817:1049가 기대빈도로 사용되어야 합니다. 이런 이유로 카이제곱 검정을 적합도(goodness of fit)이라고 부르기도 합니다. 이런 이름은 한참 뒤에 나올 CFA나 SEM과 같은 곳에서 사용될 것입니다. 지금은 이정도만 이해하면 됩니다.
1.3 이원 카이제곱(One-way \(\chi^2\) test) 검정을 계산해 보자
1.3.1 기본예제
이원 카이제곱 검정(Two-way \(\chi^2\) test)에서 Two-way란 Two-way ANOVA와 같이 변수가 2개라는 의미입니다. 두 개의 변수 모두 당연히 명목척도 (Qualitative variable)이고, 이 두 명목척도는 2개 이상의 범주(category)를 가지게 됩니다. 즉 두 개 이상의 그룹을 각 변수가 가지고 있다는 의미입니다. 변수가 두 개 이므로 당연히 데이터 코딩 시 두 개의 열(column)에 코딩해야 합니다. 이 때의 가장 단순한 형태는 \(2 \times 2\)가 될 것입니다. 즉, 각각 두 개의 그룹을 가지고 있는 두 변수를 의미 합니다. 이 경우 이를 표현하는 방법이 바로 분할표 (contingency table)입니다. 분할표란 데이터의 빈도만 표에 작성하는 것을 말하는데, 분할표는 두개의 변수를 행(Row)과 열(Column)으로 나누어 빈도를 정리합니다. 이 분할표를 통해 이원 카이제곱 검정을 할 때의 목적은 행과 열 사이에 (즉 두 변수 사이에) 어떠한 연관성이 있는지 확인해보는 것입니다.
다음은 우리가 사용할 예제입니다. 200명의 암환자를 임의 추출하여 다음의 두 가지를 조사했습니다.
- 진단받은 암이 Brain cancer인지의 여부: Yes or No
- 암을 진단받았을 때 휴대폰을 사용한지 3년 이상 되었는지의 여부: Yes or No
이를 바탕으로 다음의 \(2 \times 2\) 분할표를 작성하였습니다.
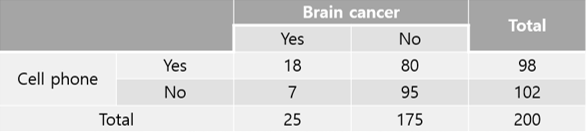
그렇다면 위의 표를 바탕으로 몇 가지 단순한 사실을 알아보겠습니다. 만약 Brain cancer와 cell phone의 사용 사이에 어떤 관련이 있으려면 전체 Brain cancer 환자의 몇 퍼센트가 3년 이상 cell phone을 사용했는지 알아볼 필요가 있습니다. 이를 통계적인 언어로 표현하면 다음과 같습니다.
\[P(CP | BC) = 18 \div 25 = 0.72\]
위에서 P()는 일반적으로 확률(Probability)를 의미합니다만, 사실 여기서는 정확하게 말하자면 Proportion이라고 보는 편이 나을 것 같습니다. 다만 설명의 편의를 위해 확률이라고 이야기하겠습니다. CP는 Cell phone을 BC는 Brain cancer를 의미합니다. 그러므로 총 Brain cancer 환자 25명 중 18명이 3년 이상 cell phone을 사용했다는 것을 알 수 있고 이를 확률로 계산해보니 72%정도가 됩니다. 반면에 다른 암 환자 중에서 3년 이상 cell phone을 사용한 사람을 조사해 보면 다음과 같습니다. 다음 암 환자 총 175명 중 80명이 3년 이상 cell phone을 사용하여 46%의 확률을 보였습니다.
\[P(CP | NBC) = 80 \div 175 = 0.46\]
이제 이원 카이제곱 검정을 계산해 보도록 하겠습니다. 일단 이 예제에서 이원 카이제곱 검정의 목적은 Brain cance와 cell phone의 연관성(association)을 알아 보는 것입니다. 여기서 조심해야 할 것이 바로 연관성이라는 단어입니다. 가끔 신문 기사나 혹은 심지어 논문 분석 결과에서 이 연관성을 인과관계로 보고 해석하는 경우가 있는데 이는 사실 조심해야할 부분입니다. 연관성이 있다와 인과관계가 있다는 비슷해 보여도 분명 다른 것입니다. 연관성이 있다고 해서 인과관계가 있는 것은 아니라는 의미입니다. 여기서는 \(2 \times 2\)분할표를 사용해서 계산할 것입니다. 이원 카이제곱 검정의 통계적 가설을 다음과 같습니다.
\[H_0: \text{Brain cancer와 cell phone 사용 간에는 연관성이 없다}\]
\[H_a: \text{Brain cancer와 cell phone 사용 간에는 연관성이 있다}\]
앞서 일원 카이제곱 검정에서 보았듯이 이 테스트를 하려면 기본적으로 데이터에서 구해진 빈도와 기대빈도(E)를 알아야 \(\chi^2\)값을 구할 수 있습니다. 기대빈도 계산법은 다음과 같습니다.
\[E(\text{기대빈도}) = \frac{\text{(Row Total)} \times \text{(Column Total)}}{\text{Grand Total}} = \frac{\text{(행합계)} \times \text{(열합계)}}{\text{총합계}}\]
위의 계산을 바탕으로 기대빈도를 작성한 표는 다음과 같습니다.
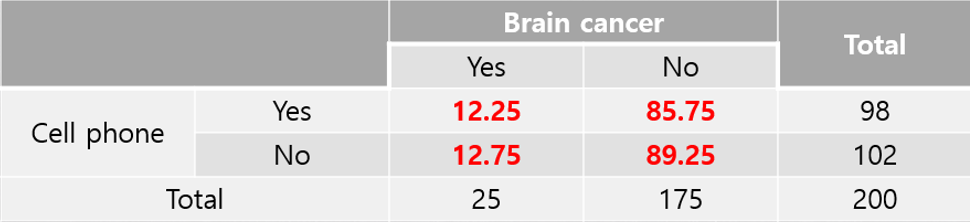
위에서 계산된 내용을 다시 살펴보면 다음과 같습니다.
\[E(CP\&BC) = \frac{98 \times 25}{200} = 12.25\]
\[E(CP\&NBC) = \frac{98 \times 175}{200} = 85.75\]
\[E(NCP\&BC) = \frac{102 \times 25}{200} = 12.75\]
\[E(NCP\&NBC) = \frac{102 \times 175}{200} = 89.25\]
이제 Figure 1.1 과 Figure 1.2 를 이용해 \(\chi^2\)값을 계산해 보겠습니다.
\[\begin{matrix} \chi^2 &=& \frac{(18-12.25)^2}{12.25} + \frac{(7-12.75)^2}{12.75} \\ && + \frac{(80-85.75)^2}{85.75} + \frac{(95-89.25)^2}{89.25} \\ &=& \small{6.048} \end{matrix}\]
\[df = (2-1) \times (2-1) = 1 \]
\[\chi^2_{df=1} = 6.048, \;p-value = 0.014\]
그러므로 Brain cancer와 cell phone 사용 간에는 어떤 연관성이 있다고 결론 내릴 수 있습니다. 물론 조심할 것은 여기서 인과관계가 있다라고 해석하면 곤란합니다. 만약 이 결과를 놓고 Brain cancer의 원인이 cell phone 사용 때문이라고 하면 이는 우리의 통계적 분석 결과를 뛰어 넘는 과도한 해석이 됩니다. 문제는 제가 한국에서 이런 논문을 꽤 많이 봤다는 사실입니다. 인과관계를 이야기 하려면 사실 이런 단순한 카이제곱 검정만으로는 부족하다고 할 수 있습니다.
1.3.2 추가예제
그렇다면 추가적인 예제를 하나 더 보겠습니다.
어떤 보험사에서 지진보험을 상품으로 판매하고 있습니다. 이 보험사는 지진의 위험성이 지역적으로 차이가 있을 것으로 보고 이에따라 지역별로 지진보험 가입 정도가 다를 가능성이 있을 것이라는 가설을 통계적으로 분석해보고자 합니다. 이를 위해 총 4 개 지역의 지진보험 가입유무를 조사한 결과를 정리한 표가 아래와 같이 있습니다.

위의 지진보험 가입현황에 대한 기대빈도는 아래와 같습니다.

위의 두 종류의 값을 이용하여 \(\chi^2\)값을 구하면 다음과 같습니다. 가능하다면 엑셀을 이용하여 직접 계산해 보는 것을 권해드립니다. 눈으로 보고 넘어가는 것 보다는 직접 계산을 해보면 보다 이해가 잘 되고 기억에도 남습니다.
\[\chi^2_{df=3} = 47.105, \; p-value < 0.05 \]
그러므로 지진보험 가입 유무는 거주지역과 연관성이 있다고 결론 내릴 수 있습니다. 다만 문제는 이 연관성 즉 지역별 가입 유무의 차이정도가 얼마나 되는지는 카이제곱 검정만으로는 알 수 없습니다. 또한 지역적 차이를 일대일로 알아내기는 불가능합니다. 이제 기본적인 카이제곱 검정은 다 알아보았습니다. 이제 카이제곱 검정과 관련이 있는 보다 어려운 내용에 대해 알아보도록 하겠습니다.
1.4 카이제곱 (\(\chi^2\) test) 검정을 넘어서
여기서는 카이제곱 검정의 전제조건과 한계점 그리고 이를 해결하기 위한 방법을 간단하게 알아보고, 카이제곱검정과 관련이 있지만 다소 복잡한 방법에 대해 알아보겠습니다. 일반적인 카이제곱 검정보다는 여기서 배우는 방법이 조금 더 낫다는 생각이 들긴 합니다.
1.4.1 전제조건
카이제곱 검정의 몇 가지 전제조건은 다음과 같습니다.
- 랜덤 샘플링: 당연한 이야기 이지만 의외로 랜덤 샘플링이라는 조건이 연구를 하다보면 쉽지 않다는 사실을 알게 됩니다.
- 독립셩
- 여기서 독립성이란 변순 내의 각 범주가 서로 상호 배타적이어야 한다는 의미입니다. 즉 한 관찰값이 여러 개의 범주에 동시에 해당될 수 없다는 의미 입니다.
- 분할표 상의 각 셀의 기대빈도는 적어도 5 이상이어야 한다.
- 그러므로 경우에 따라서는 기대빈도를 5 이상으로 맞추기 위해 볌주를 합쳐야 할 수도 있습니다.
- 만약 범주를 합치는 것이 불가능 하다면, 피셔의 정확검정을 하거나 Likelihood ratio test를 해야합니다.
1.4.2 주로 문제가 되는 경우
주로 문제가 되는 경우는 df가 1인 경우입니다. 즉 범주가 단 2 개인 경우를 의미합니다. 예를 들어 이원 카이제곱 검정을 할 때 \(2 \times 2\)인 경우가 해당됩니다. 문제는 비연속성의 조건부 확률을 연속성의 \(\chi^2\)분포에 적용함으로써 발생되는데, 이런 경우 일원 카이제곱 검정이라면 연속성을 보정하는 Yate’s correction 혹은 \(\chi^2\) continuity correction이라는 것을 해야합니다. 만약 이원 카이제곱 검정이라면 검정 결과와 Yate’s correction의 결과가 다를 경우 피셔의 정확검정을 사용하는 것이 좋습니다. 사실 이런 경우는 정확히 표현하자면 어쩔 수 없는 경우가 아니라면 카이제곱 검정을 하지 않는 것이 현실적으로는 옳은 판단일 수 있습니다.
1.4.3 상대 위험도(Relative risk)
상대 위험도란 두 확률의 차이인 \(P_1 - P_2\)가 아니라 \(P_1 \div P_2\)를 의미하고 주로 의학쪽에서 많이 사용합니다. 만약 상대 위험도가 1 이라면 두 사건이 발생할 확률은 동일하고 1보다 크다면 위험이 증가한다고 보고, 1보다 작다면 위험이 감소한다고 해석합니다.
앞서 본 예제를 다시 이용해서 상대 위험도를 설명해 보자면 다음과 같습니다.
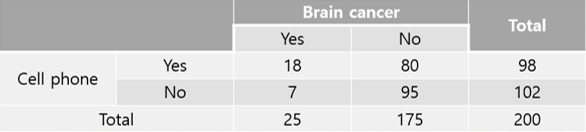
휴대폰 사용자 중 Brain cancer의 확률은 \(P(BC|CP) = 18 \div 98 = 0.184\) 이고 휴대폰 비사용자 중 Brain cancer의 확률은 \(P(BC|NCP) = 7 \div 102 = 0.069\)가 되어 상대위험도는 다음과 같습니다.
\[\text{상대위험도(Relative risk: RR)} = 0.184 \div 0.069 = 2.67\]
이는 휴대폰 사용자가 그렇지 않는 사람에 비해 약 2.67배 Brain cancer에 걸릴 확률이 높다고 해석합니다.
1.4.4 교차비 or 오즈비(Odds ratio)
오즈비를 이해하려면 먼저 오즈(odds)에 대해 알아야 합니다. 사전적으로는 오즈(odds)란 확률을 의미하지만 통계에서 오즈(odds)는 확률과 조금 다르게 계산됩니다.
\[Odds = \frac{p}{1-p}\]
여기서 \(p\)는 어떤 사건이 발생할 확률을 의미합니다. 이를 해석하기 위해 두 가지 예를 들어보겠습니다.
- 예제 1
- 만약 어떤 사건이 일어날 확률 \(p\)가 \(\frac{1}{2}\)이라면 오즈(odds)는 \(\frac{1}{2} \div \frac{1}{2} = 1\)
- 이는 어떤 사건이 일어날 확률이 \(\frac{1}{2}\)이라면 오즈(odds)가 의미하는 것은 이 사건이 일어나지 않을 확률 대비 일어날 확률은 동일하다는 의미
- 예제 2
- 만약 어떤 사건이 일어날 확률 \(p\)가 \(\frac{3}{4}\)이라면 오즈(odds)는 \(\frac{3}{4} \div \frac{1}{4} = 3\)
- 이는 어떤 사건이 일어날 확률이 \(\frac{3}{4}\)이라면 오즈(odds)가 의미하는 것은 이 사건이 일어나지 않을 확률 대비 일어날 확률은 3배 높다는 의미
그렇다면 오즈비(odds ratio)란 두 오즈(odds)의 비율을 의미합니다.
\[\theta = \frac{\frac{P(A|B)}{1-P(A|B)}}{\frac{P(A|C)}{1-P(A|C)}}\]
앞의 상대 위험도와 같은 방법으로 오즈비를 구해보겠습니다.
휴대폰 사용자 중 Brain cancer의 확률은 \(P(BC|CP) = 18 \div 98 = 0.184\) 이고 휴대폰 비사용자 중 Brain cancer의 확률은 \(P(BC|NCP) = 7 \div 102 = 0.069\)가 되어 오즈비는 다음과 같습니다.
\[\theta = \frac{\frac{P(A|B)}{1-P(A|B)}}{\frac{P(A|C)}{1-P(A|C)}} = \frac{\frac{0.184}{0.816}}{\frac{0.069}{0.931}} = \frac{0.225}{0.074} = 3.04\]
Brain cancer가 발생할 오즈는 휴대폰 사용자가 그렇지 않은 사람보다 약 3배 정도 높다는 의미가 됩니다.
이제 오즈비의 장점을 알아보겠습니다. 같은 데이터에서 만약 확률을 행에서 열로 바꾸면 어떻게 될까요? 즉, Brain cancer 환자 중에서 휴대폰 사용자의 확률과 다른 암 환자 중에서 휴대폰 사용자의 확률을 이용하면,
\[P(CP|BC) = 18 \div 25 = 0.72\]
\[P(CP|NBC) = 80 \div 175 = 0.457\]
\[\theta = \frac{\frac{P(A|B)}{1-P(A|B)}}{\frac{P(A|C)}{1-P(A|C)}} = \frac{\frac{0.72}{0.28}}{\frac{0.457}{0.543}} = \frac{2.57}{0.842} = 3.05\]
즉, 휴대폰을 가지고 있을 오즈는 Brain cancer 환자가 다른 암 환자 보다 약 3배 정도 높다는 의미가 됩니다. 결론적으로 행과 열을 바꾸어서 계산해 보아도 오즈비는 거의 비슷하게 나오는 특징이 있습니다. 결국 데이터의 영향에 매우 덜 민감한 반면, 이를 단순 오즈(odds)나 상대 위험도로 계산해 보면 크게 숫자가 변하는 것을 알 수 있습니다.
마지막으로 쉽게 \(2 \times 2\)의 오즈비를 계산하는 방법을 이야기하고 마치겠습니다.
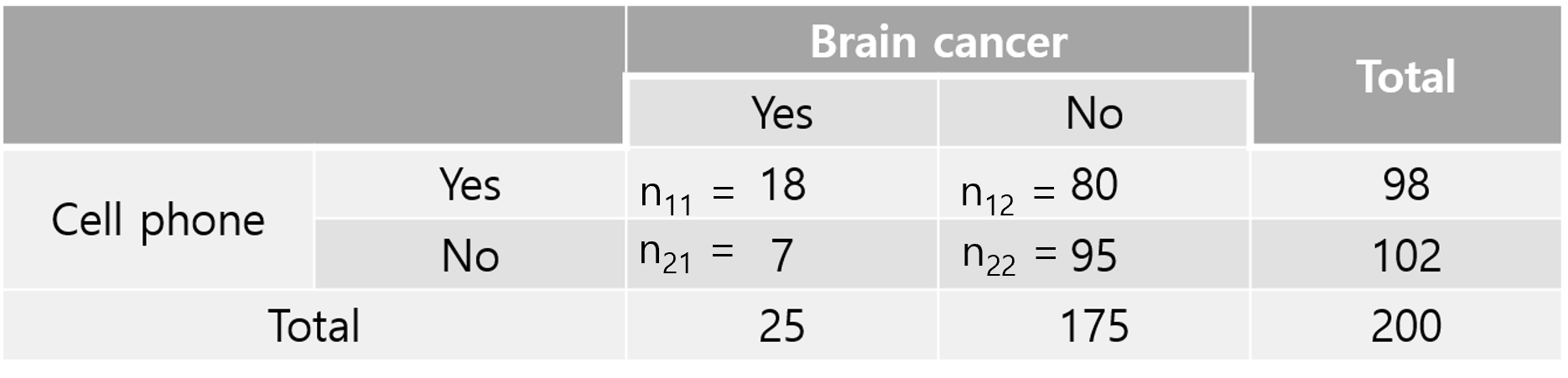
\[\theta = \frac{n_{11} \times n_{22}}{n_{12} \times n_{21}} = \frac{18 \times 95}{80 \times 7} = 3.05\]
이런식으로 계산할 수 있습니다.
1.5 카이제곱 (\(\chi^2\) test) 검정을 실습해 보자
실습용 데이터는 앞서 분산분석에서 사용한 적이 있는 Telco Customer Churn 데이터를 사용하겠습니다. 캐글(www.kaggle.com)에 들어가서 검색해 보시면 찾으실 수 있습니다. 어려우신 분들은 여기서 다운로드 받으시기 바랍니다.