3 조절효과와 매개효과
3.1 조절효과란 무엇인가?
3.1.1 조절효과의 정의
논문을 작성하다 보면 가장 많이 사용하는 두 가지가 바로 조절효과와 매개효과입니다. 조절효과는 Moderating effect라고 표현하고 조절변수를 Moderator라고 부릅니다. 이번 장에서는 조절효과와 매개효과에 대해 알아보겠습니다.
조절효과란 회귀분석에서 발견된 종속변수에 대한 독립변수의 영향력이 회귀계수의 방향이 바뀌거나 회귀계수의 크기(힘)가 변화하는 경우를 의미합니다.
- 방향이 변화한다는 것은 회귀계수가 +에서 -로 혹은 -에서 +로 바뀌는 것을 의미합니다
- 힘의 크기가 변화한다는 것은 회귀계수가 더 커지거나 작아지는 것을 의미합니다
3.1.2 조절효과의 예제
다음과 같은 간단한 예제를 하나 생각해보겠습니다.
- 종속변수: 지출(\(y_i\))
- 독립변수: 수입(\(x_i\))
- 조절변수: 성별(\(D_i\))
위의 세 개의 변수를 이용해 회귀식을 단계적으로 만들어 보겠습니다.
- 기본회귀식
- \(y_i = \alpha + \beta_1 x_i\)
- 기본회귀식 + 성별 더미변수
- \(y_i = \alpha + \beta_1 x_i + \beta_2 D_i\)
- 조절효과 회귀식
- \(y_i = \alpha + \beta_1 x_i + \beta_2 D_i + \beta_3 x_i D_i\)
문제는 위와 같이 회귀식 3개를 써 놓으면 더 이상 조절효과를 이해하지 못한다는 것입니다. 위의 세 개의 회귀식을 그림으로 그려보면서 조절효과가 의미하는 것이 무엇인지 조금 더 자세하게 알아보겠습니다.
3.1.3 그래프로 이해하는 조절효과
- 기본회귀식
- \(y_i = \alpha + \beta_1 x_i\)
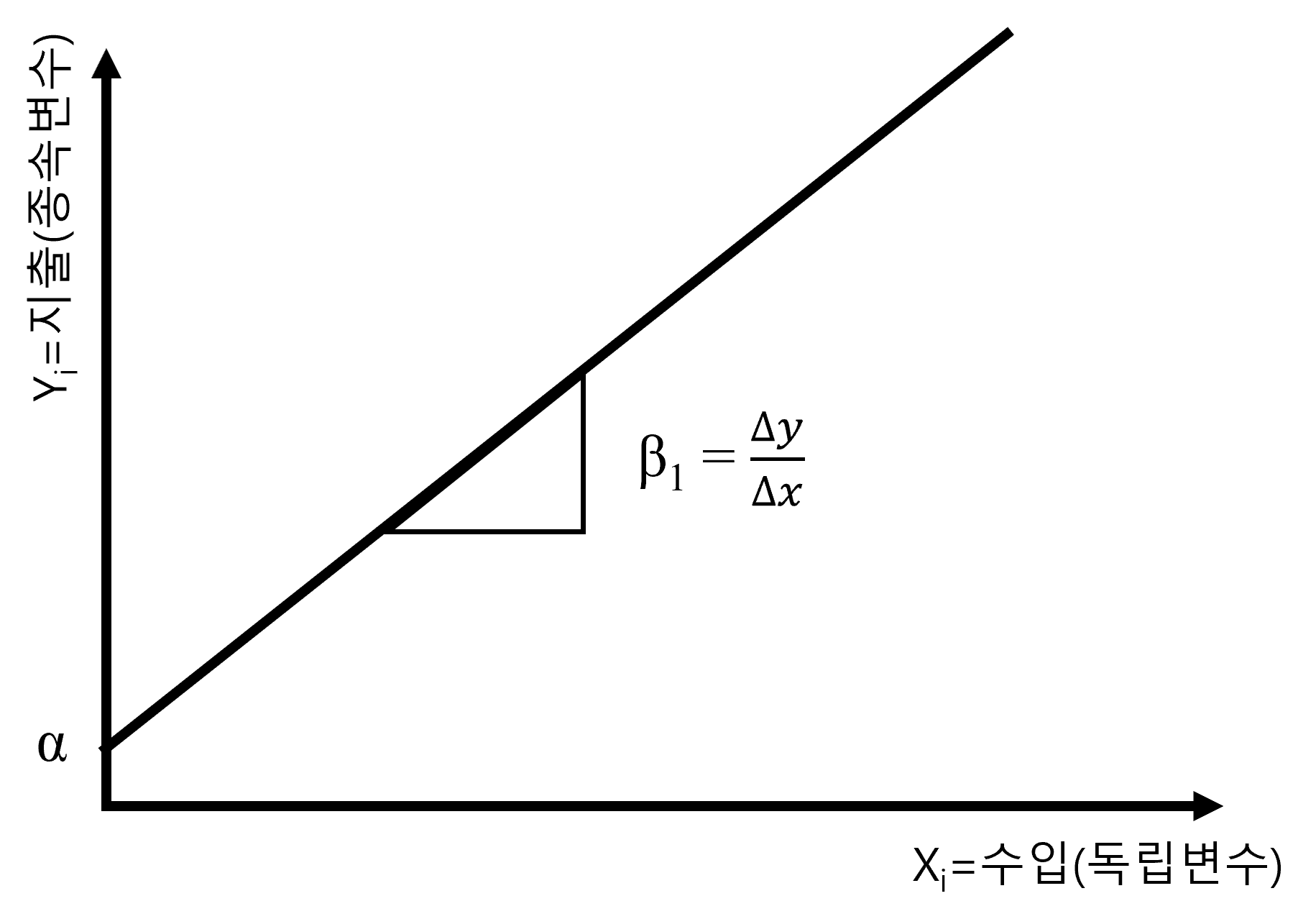
기본회귀식이 내포하는 연구가설은 독립변수 \(x_i\)인 수입이 증가할 수록 종속변수 \(y_i\) 지출이 증가할 것이라는 것입니다. 이 연구가설은 회귀계수 \(\beta_1\)에 의해 검정됩니다. 만약 \(\beta_1\)이 정의 방향으로 유의하다면 연구가설은 채택됩니다.
- 기본회귀식 + 성별 더미변수
- \(y_i = \alpha + \beta_1 x_i + \beta_2 D_i\)
그럼 이제, 기본회귀식에 성별 더미변수를 추가해보겠습니다. 여기서 성별 더미변수 \(D_i\)는 남성인 경우 \(D_i=0\)으로 여성인 경우 \(D_i=1\)로 정의 하겠습니다. 이렇게 되면 새로운 두 번째의 회귀식은 남성의 회귀식과 여성의 회귀식으로 나눠서 두 개의 회귀식을 구분할 수 있습니다.
- 남성의 회귀식: \(y_i = \alpha + \beta_1 x_i\)
- 여성의 회귀식: \(y_i = (\alpha + \beta_2) + \beta_1 x_i\)
남성의 경우 성별 더미변수 \(D_i=0\)이기 때문에 결국 기본회귀식과 동일한 회귀식이 됩니다. 반면에, 여성의 회귀식은 \(D_i=1\)이므로 \(\beta_2\)가 상수가 되어 절편 \(\alpha\)와 합쳐질 수 있습니다. 그러므로, 만약 \(\beta_2\)가 정의 방향(+)로 유의하다면, 남성의 회귀식과 여성의 회귀식은 다음과 같이 그릴 수 있습니다.
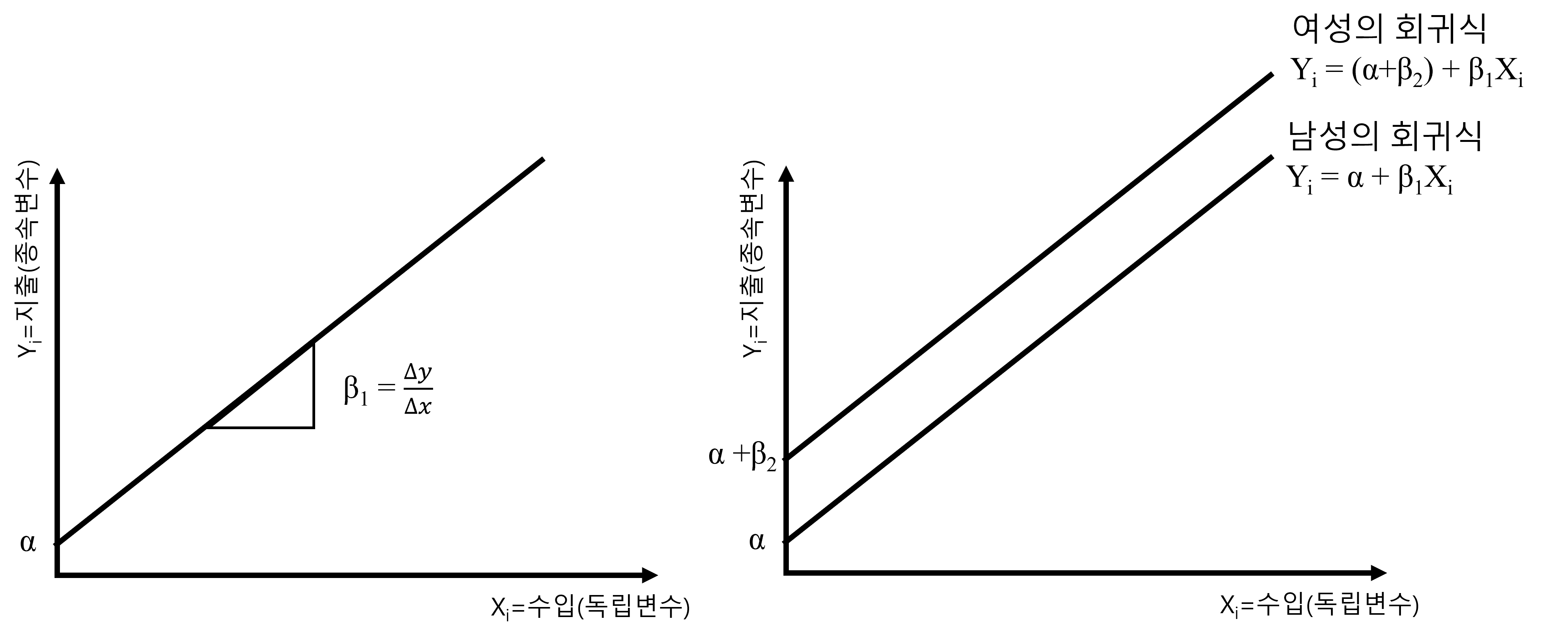
Figure 3.2 에서 보듯이 우측의 남성의 회귀식은 결론적으로는 기본회귀식과 동일하고, 여성의 회귀식은 절편이 \(\alpha\)에서 \(\alpha + \beta_2\)가 되어 \(\beta_2\)만큼 증가한 모양이 됩니다. 기울기 \(\beta_1\)은 그대로라는 점이 중요합니다. 이런 경우 연구가설을 말로 풀어서 쓴다면 어떻게 해야 할까요? 제가 이 부분을 강조하는 이유는 대부분의 학생들이 이것을 그림으로 보고 이해하는 것 같아도 실제로 연구가설을 글로 써보라고 하면 전혀 다른 말을 쓰기 때문입니다. 뿐만 아니라 결과의 해석도 이상하게 하는 경우가 많습니다.
- 연구가설: 여성이 남성에 비해 더 많이 지출할 것이다.
- 결과해석: 여성이 남성에 비해 평균적으로 \(\beta_2\)만큼 더 유의하게 지출한다.
그러므로 이 경우 \(\beta_2\)의 유의성이 의미하는 것은 절편의 증가(또는 감소)입니다. 다시 한 번, 이야기하자면 회귀분석에서 절편이 의미하는 것은 종속변수 \(y_i\)의 평균값이라는 것입니다. 즉, 여성 집단의 평균 지출 금액이 남성에 비해 평균적으로 \(\beta_2\)만큼 높다는 것입니다. 여기서 주의할 점은 이렇게 평균적으로 높은 지출금액은 수입과 관계 없이 높다는 점이 중요합니다. Figure 3.2 를 보면 여성과 남성의 두 회귀식이 평행한 것을 볼 수 있습니다. 당연히 두 회귀직선의 기울기가 동일하기 때문입니다. 따라서 이 두번째 모델 (기본회귀식+성별 더미변수)을 이용한 회귀분석의 결과를 해석할 때, 수입의 증가는 여성과 남성의 평균지출의 차이에 아무런 영향이 없다는 것입니다. 만약 수입의 증감 혹은 수입의 차이에 따라 남성과 연성의 지출 차이가 달라진다고 해석하면 잘못 해석한 것이 됩니다.
- 조절효과 회귀식
- \(y_i = \alpha + \beta_1 x_i + \beta_2 D_i + \beta_3 x_i D_i\)
위에서 한 것처럼, 여성의 회귀식과 남성의 회귀식으로 나눠보겠습니다.
- 남성의 회귀식: \(y_i = \alpha + \beta_1 x_i\)
- 여성의 회귀식: \(y_i = (\alpha + \beta_2) + (\beta_1 + \beta_3) x_i\)
위와 동일하게 남성의 회귀식은 기본회귀식과 똑같습니다. 여성의 회귀식은 두번째처럼 절편이 \(\alpha + \beta_2\)이지만, 기울기가 다릅니다. 기본회귀식과 위의 경우 모두 기울기는 \(\beta_1\)이었습니다. 그러나, 조절효과의 회귀식에서 여성의 회귀식의 기울기는 \(\beta_1 + \beta_3\)가 됩니다. 즉, \(\beta_3\)가 정의 방향(+)으로 유의하다면 여성의 회귀식의 기울기는 더 가파르게 증가하게 됩니다. 이제 그림으로 확인해 보겠습니다.
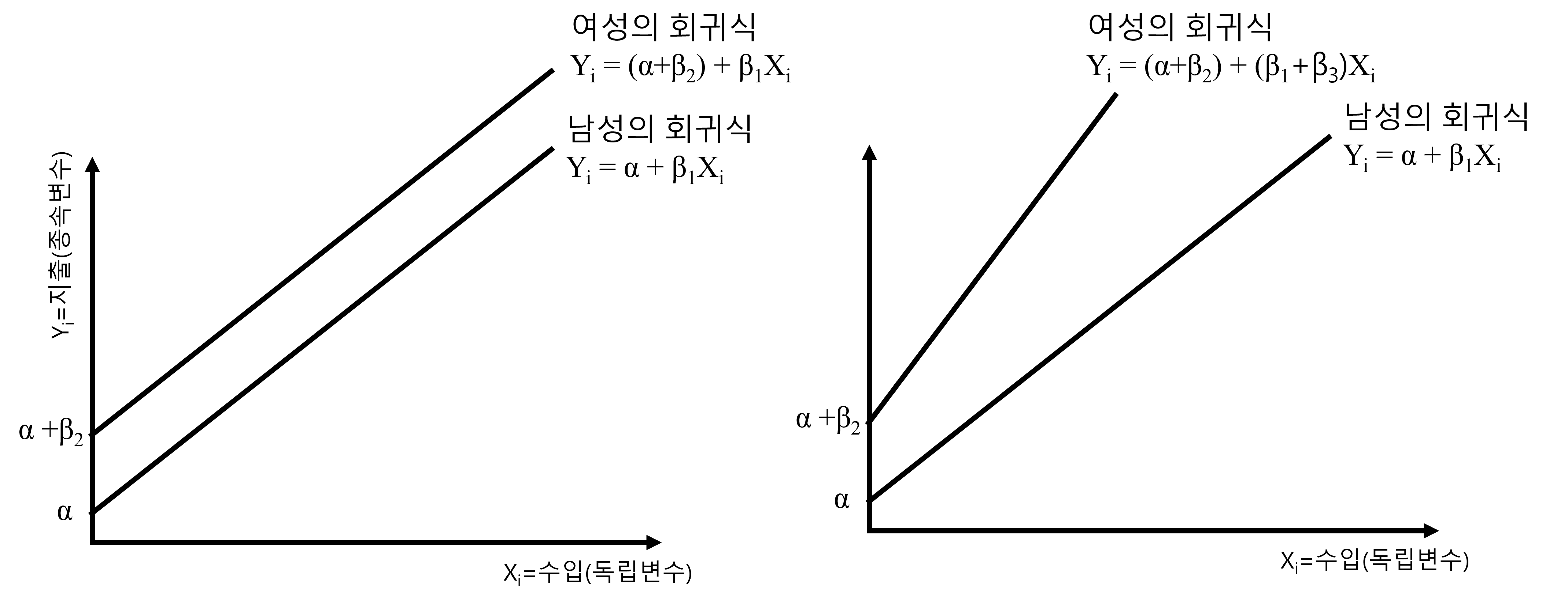
Figure 3.3 는 기본회귀식에 성별더미만 추가한 경우(좌측)와 조절회귀식의 경우(우측)를 비교해서 보여줍니다. 우측에서 보는 것처럼 여성의 회귀식의 기울기가 더 가파르게 증가하는 것을 볼 수 있습니다. 즉, 기울기가 \(\beta_3\)더 빠르게 증가하는 것입니다. 이를 어떻게 해석해야할 까요?
우선 앞의 경우와 동일하게 여성이 남성에 비해 평균적으로 \(\beta_2\)만큼 더 지출하고 있는 것은 동일합니다. 여기에 더해 여성은 남성에 비해 수입이 동일하게 1단위 증가한다 할지라도 \(\beta_3\)만큼 더 지출한다는 의미가 됩니다. 여기서 수입 1단위는 데이터상에서 수입의 기본 단위(unit)를 의미합니다. 만약 조사가 100만원 단위로 이루어졌고 \(\beta_3 = 12\)라면 여성은 남성에 비해 수입이 동일하게 100만원 증가한다 할지라도 평균적으로 12만원을 더 지출한다는 의미가 됩니다. 좀 더 자세하게 해석하자면, 만약 \(\beta_1=60\)이었다고 가정하면, 남성은 수입이 100만원 증가할 때, 평균적으로 60만원의 지출이 더 증가하지만, 어성은 동일하게 수입이 100만원 증가할 때, 평균적으로 지출이 72만원 증가한다는 의미가 됩니다.
3.1.4 조절효과에 대한 정리
- 조절효과를 확인하기 위해서는
- 기존의 독립변수에 조절변수를 추가적인 독립변수로 투입하고
- 독립변수와 조절변수를 곱한 교호작용변수 (interaction)을 투입하여
- 교호작용변수가 유의한지 확인합니다
- 만약, 교호작용변수가 유의하면 조절효과가 있다고 판단합니다
- 조절효과가 중요한 이유
- 조절효과는 선형관계를 확인하는 회귀분석에서 비선형관계를 알 수 있는 중요한 방법이기 때문입니다
여기서 비선형 관계란 무엇일까요? 앞에서도 몇 번 이야기한적 있지만 선형관계 즉 linear relationship이란 독립변수와 종속변수의 관계가 직선적인 것을 의미합니다. 직선적이란 회귀분석에서 기울기 \(\beta\)가 변하지 않는 것을 의미합니다. 기울기가 독립변수의 값의 크기에 관계없이 일정한 것이 바로 회귀분석에서의 선형관계입니다.
그런데, 조절변수가 등장하면서 이 선형관계가 변합니다. 위의 예에서는 수입과 지출의 선형관계가 성별이라는 더미변수에 의해 변화하는 것입니다. 왜냐하면 성별에 따라 즉 남성과 여성의 회귀식의 기울기가 달라졌기 때문입니다. 여기서 다시 말씀드리자면 남성과 여성의 회귀식이 다르다는 표현을 통계에서 사용하려면 남성과 여성의 회귀식이 같은지 다른지 테스트를 해야합니다.
- \(y_i = \alpha + \beta_1 x_i + \beta_2 D_i + \beta_3 x_i D_i\)
- 남성의 회귀식: \(y_i = \alpha + \beta_1 x_i\)
- 여성의 회귀식: \(y_i = (\alpha + \beta_2) + (\beta_1 + \beta_3) x_i\)
아마도 어떤 분들은 그렇게 질문하실지도 모르겠네요. 아니 언제 남성과 여성의 회귀식 기울기가 같은지 다른지 테스트 한적이 있나요? 별도의 테스트를 한적이 없는데요? 사실 이게 헷갈리수도 있는데 우리는 이미 테스트를 마쳤습니다. 위의 회귀식을 다시 보면, 남성 회귀식의 기울기는 \(\beta_1\)이고 여성 회귀식의 기울기는 \(\beta_1 + \beta_3\)입니다. 그러면 두 회귀식의 차이는 기울기 \(\beta_3\)입니다.
원래의 회귀식을 보면 가장 마지막의 변수 \(x_i D_i\)가 교호작용 변수 쉽게 interaction인데 이변수가 유의한지 아닌지를 보면 조절효과가 있는지 없는지 알 수 있습니다. 왜냐하면 이 interaction의 회귀계수가 \(\beta_3\)이기 때문입니다. 그러므로, 만약 \(\beta_3\)가 유의하면 조절효과가 유의한 것이고, \(\beta_3\)가 유의하지 않다면 조절효과가 유의하지 않은 것입니다.
헷갈리면 안되는 것이 우리가 테스트 하는 회귀식은 단 하나의 조절회귀식입니다. 이 회귀식을 가지고 통계 프로그램에서 회귀분석을 하는 것이지 남성회귀식 여성회귀식을 따로 돌리는 것이 아닙니다. 이미 조절회귀식 한 번만 돌리면 그리고 마지막의 interaction 변수의 회귀계수 \(\beta_3\)가 유의한지 아닌지만 보면 조절효과가 유의한지 아닌지 알 수 있는 것이지요.
3.1.5 추천논문
제가 조절효과와 매개효과에 대해 강의할 때마다 학생들에게 제발 한 번만 읽어보라고 하는 논문이 바로 Baron & Kenny(1986) 논문입니다. 물론 최근에 와서는 이 Baron & Kenny (1986) 논문이 너무 과도하게 사용되고 또한 문제점이 지적되면서 인용이 줄고 있기는 하지만 여전히 조절효과와 매개효과에 대한 이해를 위해서는 가장 잘 설명되어 있고 쉽게 풀어 놓은 논문입니다. 영어이긴 하지만 매우 쉬운 영어로 되어있어 꼭 한번 읽어보시길 바랍니다. Google Scholar에 가서 검샣해보면 인용횟수도 볼 수 있습니다. 더불어 무료로 볼 수 있는 유명한 논문입니다.
Baron, R. M., & Kenny, D. A. (1986). The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of personality and social psychology, 51(6).
이제 그럼 조절효과를 실습해 보도록 하겠습니다.
3.2 조절효과를 실습해 보자
앞에서 했던 데이터로 계속 실습해 보도록 하겠습니다.
사용할 테이터와 변수
- House sales price in Kings County, USA (Kaggle.com) 다운로드
- 종속변수: price (= 매매 가격)
- 독립변수: floors (= 층수)
- 조절변수: waterfront (= 강/호수/바다 근접 유무)
연구가설
- \(H_1\): 주택의 가격은 주택의 층수가 증가하면 정의 방향으로 증가할 것이다
- \(H_2\): 주택의 층수가 같아도 물가에 있으면 가격이 더 높을 것이다
연구가설 1은 독립변수 층수와 종속변수 가격의 관계를 규정한 가설이고, 연구가설 2번이 연구가설 1의 층수와 가격의 관계를 물가의 유무가 조절한다는 조절변수에 대한 가설입니다.
최근 Andrew Hayes의 Process 때문에 더 유명해지긴 했는데, 사실 이미 오래된 방법 중의 하나가 연구모형을 conceptual model와 statistical model로 나누어 리포트 하는 것입니다. 연구모델이 간단할 때는 꽤 좋은 방법이지만 사실 모형이 복잡하고 변수가 많으면 그다지 깔끔해 보이지 않습니다. 조절효과의 conceptual model과 statistical model은 다음과 같습니다.
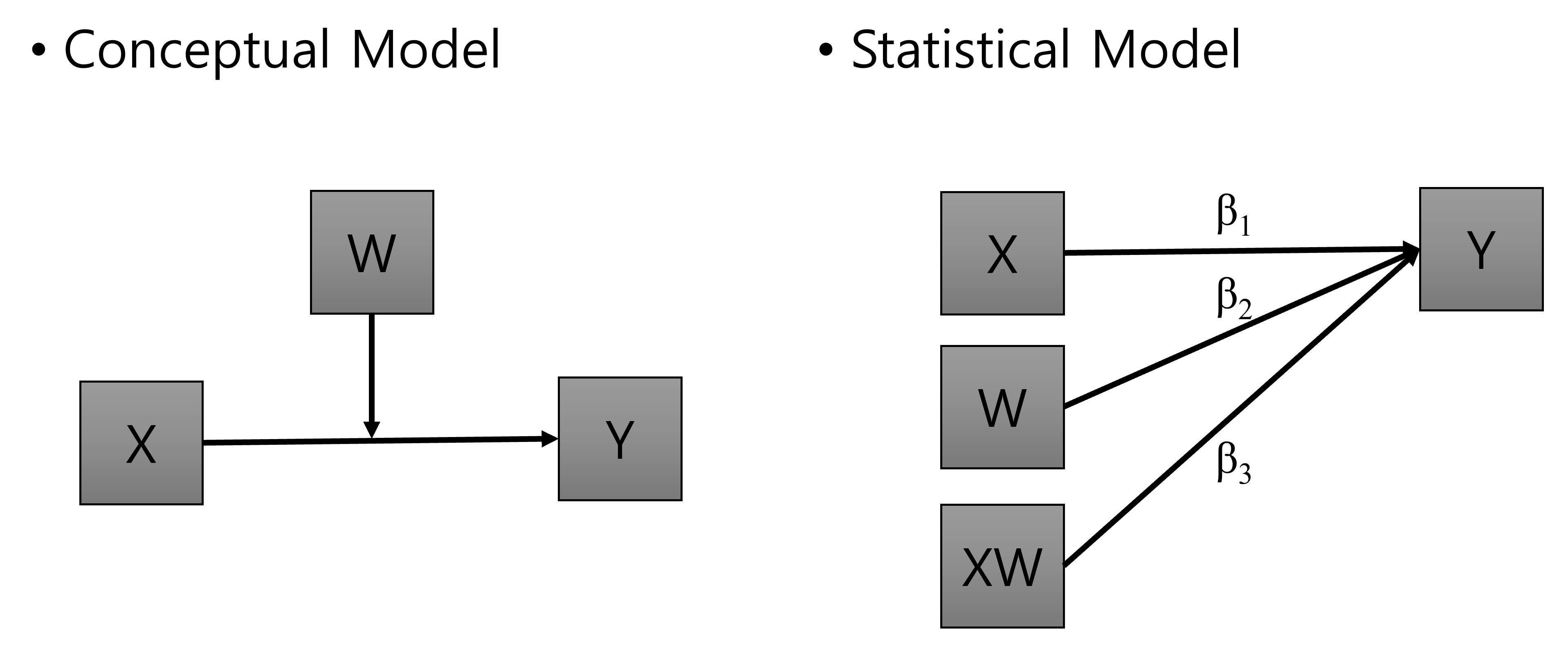
Figure 3.4 에서 X 는 독립변수를 Y는 종속변수를 W는 조절변수를 의미합니다. Statistical model에서 XW는 독립변수와 조절변수의 interaction 변수를 의미하고 화살표는 인과관계를 그리고 \(\beta_i\)는 회귀계수를 의미합니다.
이제 실습을 통해 조절효과를 마무리해 보도록 하겠습니다.
3.3 매개효과란 무엇인가?
3.3.1 매개효과의 의미와 중요성
매개효과란?
- 독립변수가 종속변수에 유의한 영향을 미칠 때,
- 독립변수와 종속변수 사이에서 매개하는 변수인 매개 변수를 통해 그 영향이 순차적으로 전달 되는 경우
- 독립변수 X, 종속변수 Y 그리고 매개변수 M으로 정의할 때,
- \(X \longrightarrow M \longrightarrow Y\)
- 이때 중간의 변수 M을 매개변수라고 함
매개변수가 중요한 이유는 상황에 따라 다르나, 매개의 종류에 의해 매개 변수 없이는 독립변수의 영향이 종속변수까지 도달하지 못하는 경우가 있어 매우 중요한 효과라고 할 수 있습니다.
3.3.2 매개효과의 종류
매개효과는 두 가지가 있습니다.
- 완전매개효과 (Full Mediation)
- 부분매개효과 (Partial Mediation)
완전매개효과는 독립변수(X)와 종속변수(Y) 사이의 관계가 매개변수(M)를 통해서만 전달되는 경우를 의미하고, 부분매개효과는 매개변수(M)를 통해 전달되는 것이 있지만, 독립변수(X)와 종속변수(Y) 사이에 직접적인 관계도 존재하는 경우를 의미합니다.
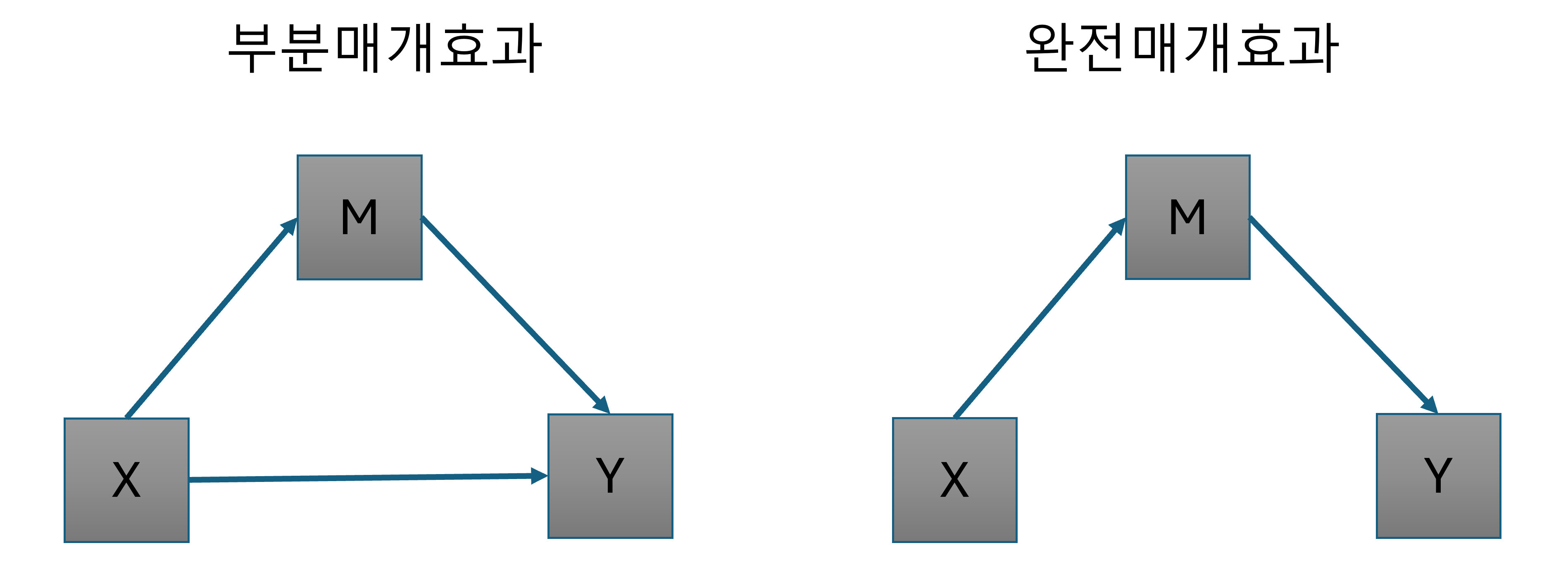
Figure 3.5 에서 부분매개효과는 매개변수를 통해 독립변수의 효과가 전달되면서 동시에 독립변수와 종속변수 사이에 직접적인 효과가 있다는 것이 화살표를 통해 알 수 있습니다. 여기서 매개변수를 통해서 전달되는 효과를 간접효과라고 부르고, 독립변수에서 종속변수로 직접 영향을 미치는 효과를 직접효과라고 부릅니다. 그러므로 완전매개효과는 직접효과는 없고 간접효과만 존재하는 것을 의미합니다.
\[ 직접효과 (Direct Effect): X \longrightarrow Y \]
\[ 간접효과 (Indirect Effect): X \longrightarrow M \longrightarrow Y \]
여기서 이 두 효과 즉 직접효과와 간접효과를 합친 것을 총효과(Total Effect)라고 부릅니다.
\[ 총효과 (Total Effect): 직접효과(Direct Effect) + 간접효과(Indirect Effect) \]
3.3.3 매개효과 검정방법
Baron & Kenny (1986) 방법을 통해 매개효과를 검증할 수 있습니다. 가장 많이 알려진 오래된 방법입니다. 다만, 2000년대 이후 이 Baron & Kenny (1986)의 방법이 많은 문제점이 있어서 이를 보완한 방법이 제안되었습니다. 하지만, 전통적인 방법을 먼저 이해하는 것이 중요하므로 이에 대해 알아보도록 하겠습니다.
- 회귀분석 3단계 방법 (일명, Baron & Kenny의 방법)
- 1단계: \(X \longrightarrow M\)
- 2단계: \(X \longrightarrow Y\)
- 3단계: \(X + M \longrightarrow Y\)
- 단계별 회귀분석 결과 해석 방법
- 1단계: X는 M에 대해 무조건 유의해야 함
- 2단계: X는 Y에 대해 무조건 유의해야 함
- 3단계: 2단계 회귀식에 매개변수 M이 새로이 추가된 상황에서 M은 무조건 유의해야 함
- X가 2단계에서는 유의했으나 3단계에서 유의하지 않으면 M은 완전매개
- X가 2단계와 3단계에서 모두 유의하면 M은 부분매개
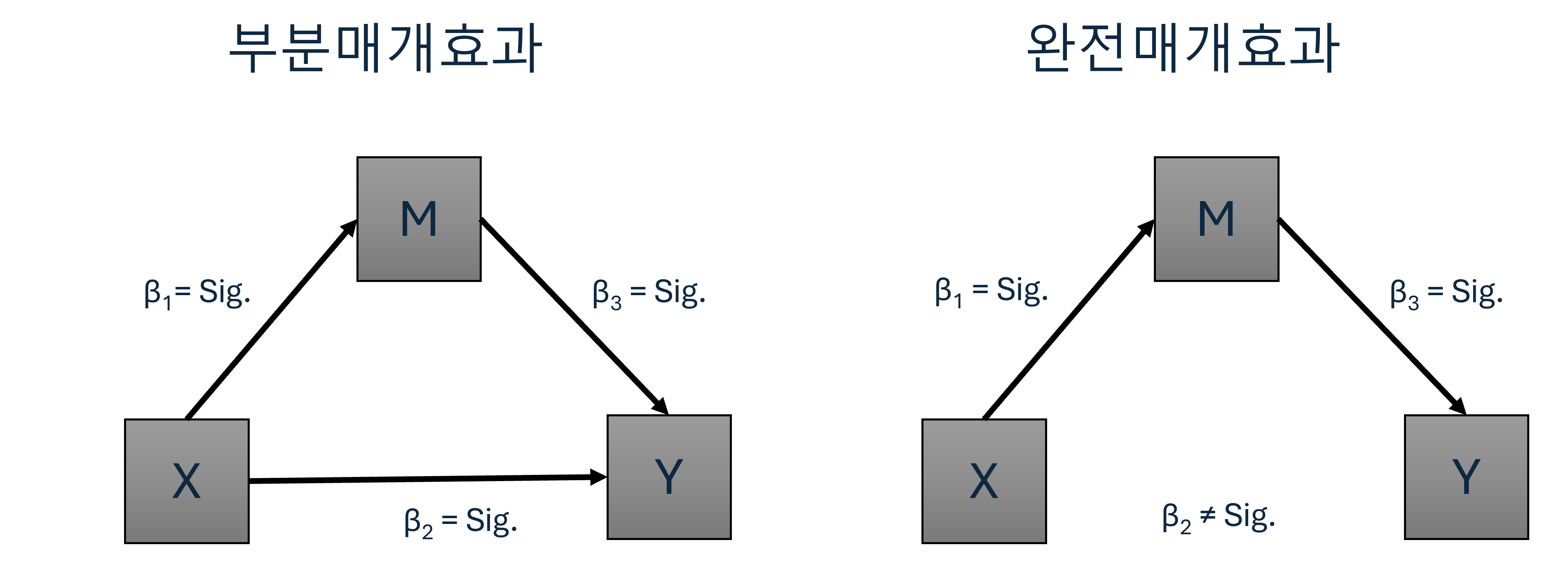
Figure 3.6 을 통해 좀 더 자세하게 알아봅시다.
우선 부분매개효과를 단계별로 다시 알아보면,
- 1단계
- \(M = \alpha + \beta_1 X\)
- 매개변수 M을 종속변수로 놓고 X를 독립변수로 하는 회귀분석을 하면,
- 독립변수 X의 회귀계수인 \(\beta_1\)이 무조건 유의해야 합니다
- 2단계
- \(Y = \alpha + \pi X\)
- 종속변수 Y, 독립변수 X로 놓고 회귀분석을 했을 때,
- 독립변수 X의 회귀계수인 \(\pi\)가 무조건 유의해야 합니다
- 3단계
- \(Y = \alpha + \beta_2 X + \beta_3 M\)
- 2단계의 회귀분석에 매개변수 M을 추가하여 회귀분석을 하면,
- 매개변수의 회귀계수인 \(\beta_3\)가 무조건 유의하고 동시에 \(\beta_2\)가 유의하면
- 이를 부분매개라고 합니다
부분매개에서 총효과는 다음과 같습니다.
- 총효과란 직접효과와 간접효과의 합
- 직접효과: \(\beta_2\)
- 간접효과: \(\beta_1 \times \beta_3\)
- \(총효과 = 직접효과 + 간접효과 = \beta_2 + (\beta_1 \times \beta_3)\)
다음으로 완전매개효과에 대해 알아봅시다. 단계별로 완전매개효과를 알아보는 방법 자체는 앞의 부분매개효과를 알아보는 방법과 동일합니다. 다만 3단계의 결과가 다르다고 보면 됩니다.
- 1단계
- \(M = \alpha + \beta_1 X\)
- 매개변수 M을 종속변수로 놓고 X를 독립변수로 하는 회귀분석을 하면,
- 독립변수 X의 회귀계수인 \(\beta_1\)이 무조건 유의해야 합니다
- 2단계
- \(Y = \alpha + \pi X\)
- 종속변수 Y, 독립변수 X로 놓고 회귀분석을 했을 때,
- 독립변수 X의 회귀계수인 \(\pi\)가 무조건 유의해야 합니다
- 3단계
- \(Y = \alpha + \beta_2 X + \beta_3 M\)
- 2단계의 회귀분석에 매개변수 M을 추가하여 회귀분석을 하면,
- 매개변수의 회귀계수인 \(\beta_3\)가 무조건 유의하지만, \(\beta_2\)가 유의하지 않을 경우
- 이를 완전매개효과라고 합니다
완전매개에서 총효과는 다음과 같습니다.
- 총효과란 직접효과와 간접효과의 합이므로,
- 직접효과: \(\beta_2\) = 0가 되어 직접효과는 없습니다
- 간접효과: \(\beta_1 \times \beta_3\)
- \(총효과 = 직접효과 + 간접효과 = 0 + \beta_1 \times \beta_3\)
3.3.4 3단계 매개효과 검증방법의 문제점
사실 Baron & Kenny (1986)의 3단계 검정방법은 현재로선 거의 전설에 가까운 오래된 방법입니다. Baron & Kenny (1986)의 논문을 읽어보면 정말 간단 명료하면서도 이해가 잘되게 설명을 잘했습니다. 이 방법이 현재까지 우리나라를 포함한 여러 나라에서 가장 많이 사용되는 방법임에는 분명하지만, 2000년대를 넘어가면서 이 방법에 대한 문제점을 지적하는 논문들이 하나 둘씩 등장하기 시작합니다. 가장 많이 지적되는 것이 Baron & Kenny (1986)의 방법은 매개효과를 검증하는 방법이 직접적인 것이 아닌 간접적인 것이라는 점입니다. 단 한 번의 통계적 검정과정을 거친 것이 아니라, 단계별로 조건을 전제로 하기 때문에 불완전하다는 것입니다.
분명히 맞는 말이긴 합니다만, 매개효과를 이해하고 이를 초보자적인 수준에서 검증하기에는 이보다 좋은 방법은 없습니다. 이후에 이를 보완하는 차원에서 보다 직접적인 검증방법이 등장합니다. 바로 Sobel test입니다. 소벨 테스트는 매해효과의 유의성을 보다 직접적으로 검정하기 위한 방법입니다.
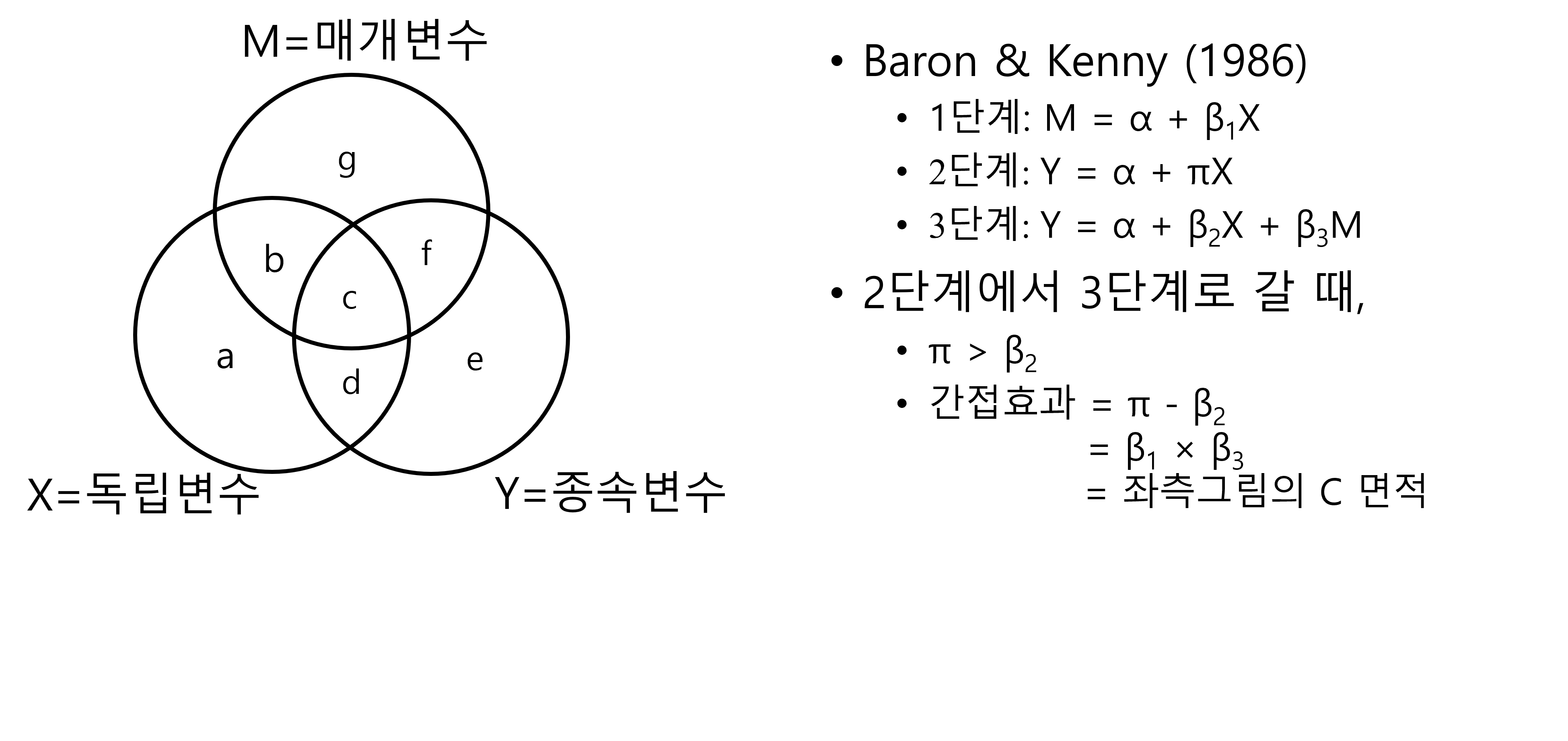
Figure 3.7 에서 보는 것처럼, 매개효과란 결론적으로 독립변수 X, 종속변수 Y, 그리고 매개변수 M이 동시에 겹치는 분산인 c 부분을 의미합니다. 3단계 방법에서 2단계의 회귀계수 \(\pi\)는 사실상 독립변수 X의 종속변수 Y에 대한 총효과를 의미합니다. 왜냐하면 매개변수 M이 없기 때문입니다. 그런 이유로 당연히 3단계의 회귀계수 \(\beta_2\)는 무조건 \(\pi\) 보다 작아야 합니다. 왜냐하면 3단계의 \(\beta_2\)는 독립변수 X의 직접효과이고, 3단계의 회귀계수 \(\beta_3\)는 매개변수 M의 종속변수 Y에대한 효과이기 때문입니다. 정확하게는 간접효과는 1단계의 회귀계수 \(\beta_1\)과 3단계의 회귀계수 \(\beta_3\)의 곱이기 때문입니다.
Baron & Kenny (1986)의 문제점은 이 간접효과부분 즉 Figure 3.7 의 \(c\)부분에 대한 통계적 검정을 하지 않았다는 것입니다. 그렇다면 이를 통계적으로 검정하는 소벨테스트는 어떻게 하는 것일까요?
3.3.5 Sobel 테스트
소벨 테스트를 위해 필요한 것은 4가지 입니다.
- Baron & Kenny (1986)의 1단계의 회귀계수 \(\beta_1\)
- Baron & Kenny (1986)의 1단계의 회귀계수 \(\beta_1\)의 표준오차 \(SE_{(\beta_1)}\)
- Baron & Kenny (1986)의 3단계의 회귀계수 \(\beta_3\)
- Baron & Kenny (1986)의 3단계의 회귀계수 \(\beta_3\)의 표준오차 \(SE_{(\beta_3)}\)
기본적으로 소벨테스트는 z-test로 볼 수 있습니다. 제가 유투브 강의안에는 t-value라고 적었는데 사실 책마다 조금씩 다르게 나와서 저도 조금 헷갈리기는 합니다만, 대부분의 경우 z-value를 이야기 합니다. 계산 공식은 다음과 같습니다.
\(Sobel \; z-value = \frac{\beta_1 \times \beta_3}{\sqrt{(\beta_1^2 \times SE_{\beta_3}^2) + (\beta_3^2 \times SE_{\beta_1}^2)}}\)
계산 방법이 복잡하지는 않지만 꽤 귀찮은 편입니다. 특히 분모의 부분이 교차하면서 곱해지는 것을 헷갈리면 안됩니다. 요즘은 구글링 하면 자동으로 계산해주는 웹 페이지도 많고, 그다지 어렵지 않은 것이라 소프트웨어가 해결해 주는 경우가 많습니다.
재미있는 것은 이 Sobel test는 1982년에 발표된 것으로 사실 Baron & Kenny (1986) 보다 먼저 나왔다고 볼 수 있습니다. 그런데, 사실 프로세스적으로 본다면 Sobel test가 Baron & Kenny (1986)을 기반으로 만들어진 것처럼 보이는 것이 사실입니다. 쉽게 말해 둘의 베이스는 거의 같다고 보면 될 것 같습니다.
문제는 이렇다보니 Sobel test도 문제가 있다는 것입니다. Figure 3.7 을 다시 보면 결국 총효과에서 직접효과를 뺀 것이 간접효과 이므로 다음과 같이 표현할 수 있습니다.
\[ \pi - \beta_2 = \beta_1 \times \beta_3\]
문제는 만약 위의 좌항과 우항이 다를 경우입니다. 즉, 총효과에서 직접효과를 뺀 나머지가 간접효과가 아니라면 문제가 되는 것이지요. 이런 일이 있을까 싶지만 꽤 자주 발생합니다. 이유는 두 회귀계수의 cross product인 \(\beta_1 \times \beta_3\)의 분포가 불확실하기 때무입니다. 사실 이 cross product의 분포는 데이터의 분포와는 별개의 문제이기도 합니다. 회귀계수의 곱의 결과물의 분포라는게 쉽게 이해가 되지 않지만, 실제로 이런 문제가 발생한다는 것이지요. 즉, 완벽하지는 않다는 의미입니다.
3.3.6 그렇다면 어떻게?
이러한 문제를 해결하는 방법이 바로 Bootstraping 입니다.
이 또한 깊이 들어가면 복잡한 문제인데, 쉽게 말해 반복 샘플링을 하는 시뮬레이션을 한다고 보면 비슷합니다. 이렇게 반복 샘플링을 해서 테스트를 하면, 95% confidence interval을 구하게 되는데, 이때 숫자 0이 이 interval 안에 포함되면 매개효과는 0이라는 의미가 되므로 매개효과는 없는 것이고, 0이 포함되지 않는 interval이 나오면 매개효과는 유의하다고 판단합니다.
과거에는 이 방법이 구현하기 어렵기도 하고, 소프트웨어나 컴퓨터 성능이 뒷받침이 되지 않아서 거의 불가능 했으나, 지금은 쉽게 소프트웨어가 값을 구해줍니다. 참 좋은 세상입니다.
가능하다면 제 개인적으로는 Baron & Kenny (1986)의 3단계 방법과 소벨 테스트 그리고 부트스트래핑 모두를 테스트 해보실 것을 권합니다. 왜냐하면 이제는 발전된 소프트웨어와 컴퓨팅 능력 덕분에 쉽게 테스트 해볼 수 있기 때문입니다.
이제 매개효과도 끝이 났네요. 실습을 해보도록 하겠습니다.
3.4 매개효과를 실습해 보자
그럼 이제 매개효과를 실습해 보도록 하겠습니다.
실습 데이터는 다음과 같습니다.
- Kaggle.com에서 다운로드
- Github에서 다운로드
- 실습모형과 변수
- 독립변수: Dalc (workday alcohol consumption: from 1 to 5)
- 매개변수: studytime (weekly study time)
- 종속변수: failures (number of class failures)
단순하게 설명하자면 술을 먹으면 학습시간이 줄고 클래스에서 fail할 가능성이 높을 것이라는 가설을 세우고 이를 매개효과로 검증해보고자 하는 것입니다. 물론 연습용이다 보니, 가설이 좀 성급하게 만들어진 느낌이 있긴 합니다. 다만, 논리적으로 큰 문제가 없어보이므로 분석을 진행해 보겠습니다.

결과를 살펴보면, 1단계에서 독립변수 Dalc가 매개변수 studytime에 마이너스로 유의한 것을 확인할 수 있습니다. 즉, 술을 많이 마실수록 공부시간이 줄어드는 것이 맞다고 볼 수 있겠습니다. 2단계에서는 독립변수 Dalc가 종속변수 failures에 플러스로 유의합니다. 즉, 술믈 많이 마실수록 클래스에서 fail할 가능성이 더 높아지는 것이지요. 마지막으로 3단계서는 매개변수 studytime의 추가 투입에도 불구하고 독립변수 Dalc는 여전히 유의하고, 추가된 매개변수 studytime 또한 유의합니다. 결론적으로 부분매개효과가 있다고 볼 수 있습니다.
총효과는 \((-0.1847 \times -0.1354) + 0.0886 \approx 0.025 + 0.0886 = 0.1136\)가 됩니다.
Sobel 테스트를 해보면, 다음과 같습니다.
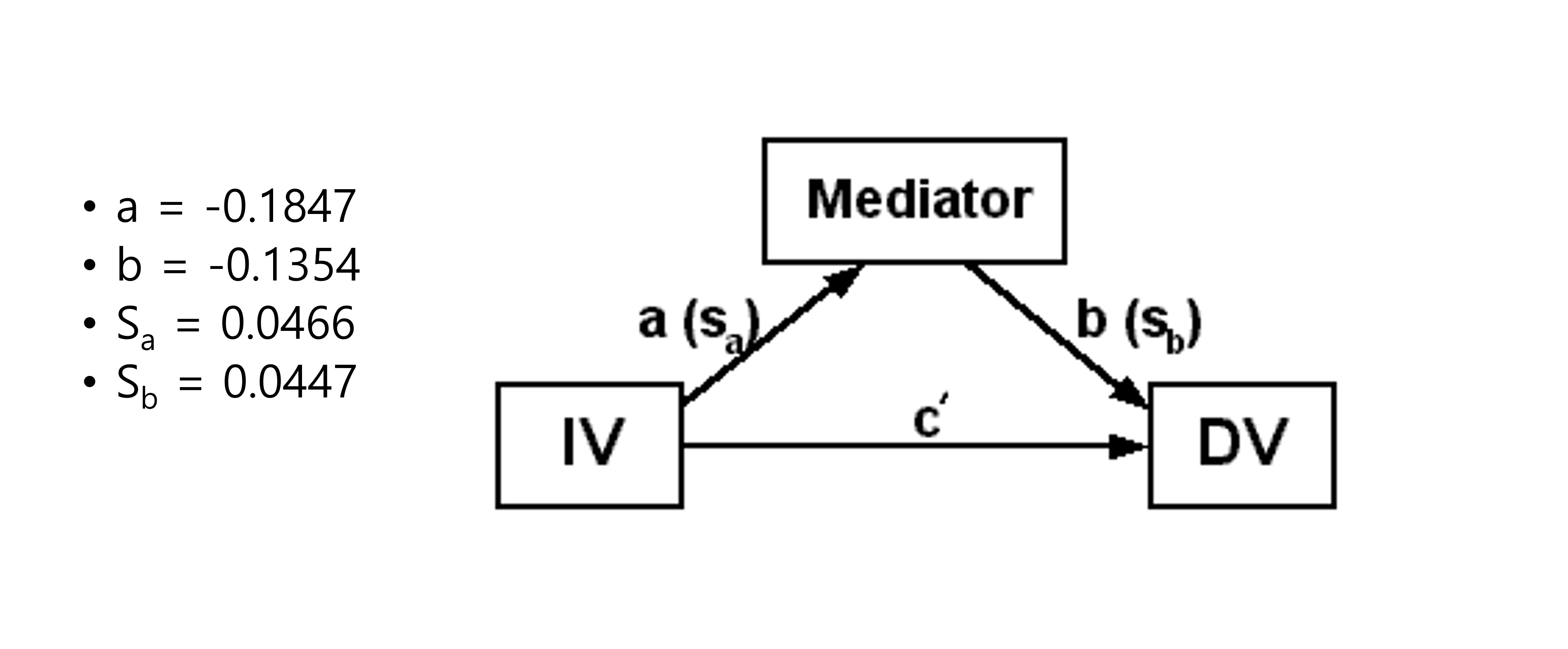
소벨테스트를 위한 4개의 값은 Figure 3.9 와 같습니다. 이를 테스트하기 위해 구글에서 간단하게 검색을 해보면 다음과 같은 웹이 있습니다. 여러분들은 다른 웹에서 테스트 해보셔도 좋습니다.

그럼 아래의 링크를 이용해 실습을 해보시길 바랍니다. 고생 많으셨습니다.