2 회귀분석

2.1 회귀분석이란 무엇인가?

2.1.1 회귀분석이란?

흔히 회귀분석을 통계의 꽃이라고 부릅니다. 사실 여태 공부한 내용은 모두 회귀분석을 위해 공부한 것이라고 해도 과언이 아닙니다. 문제는 많은 경우 회귀분석이 중요한 분석방법이라는 것은 잘 알고 있으면서도 중요한 것들은 정작 놓치고 있다는 사실입니다. 이제 회귀분석을 공부해 봅시다. 회귀분석을 이해하려면 먼저 이 방법의 이름부터 좀 이해하고 시작해야 합니다. 회귀분석은 영어로 Regression Analysis라고 부릅니다. 회귀란 단어나 Regression이란 단어 모두 같은 의미입니다. 회귀한다는 것은 어딘가로 되돌아간다는 의미입니다. 요즘 제가 좋아하는 웹툰들은 모두 회귀를 주제로 하더군요. 요즘 웹툰의 트렌드인가 싶긴합니다.

그렇다면 도대체 어디로 되돌아간다는 것일까요? 어디로 회귀한다는 것일까요? 정답을 먼저 이야기 하자면 바로 평균으로의 회귀입니다. 사실 회귀분석은 평균과 관련된 이야기입니다. 그럼 회귀분석의 목적은 무엇일까요? 회귀분석은 기본적으로 예측(forecasting)이 목적입니다. 좀 더 자세하게 말하자면 독립변수로 종속변수를 예측하고자 하는 것이 기본적인 목적입니다. 일반적으로 독립변수가 1개이면 단순회귀분석, 독립변수가 여러 개인 경우 다중회귀분석이라고 합니다. 혹시라도 종속변수의 개수가 궁금하신 분들을 위해 더 자세하게 말씀드리자면 회귀분석에서는 종속변수는 무조건 1개입니다.

2.1.2 회귀분석의 예제

회귀분석을 이해하기 위해 예를 하나 들어보겠습니다.

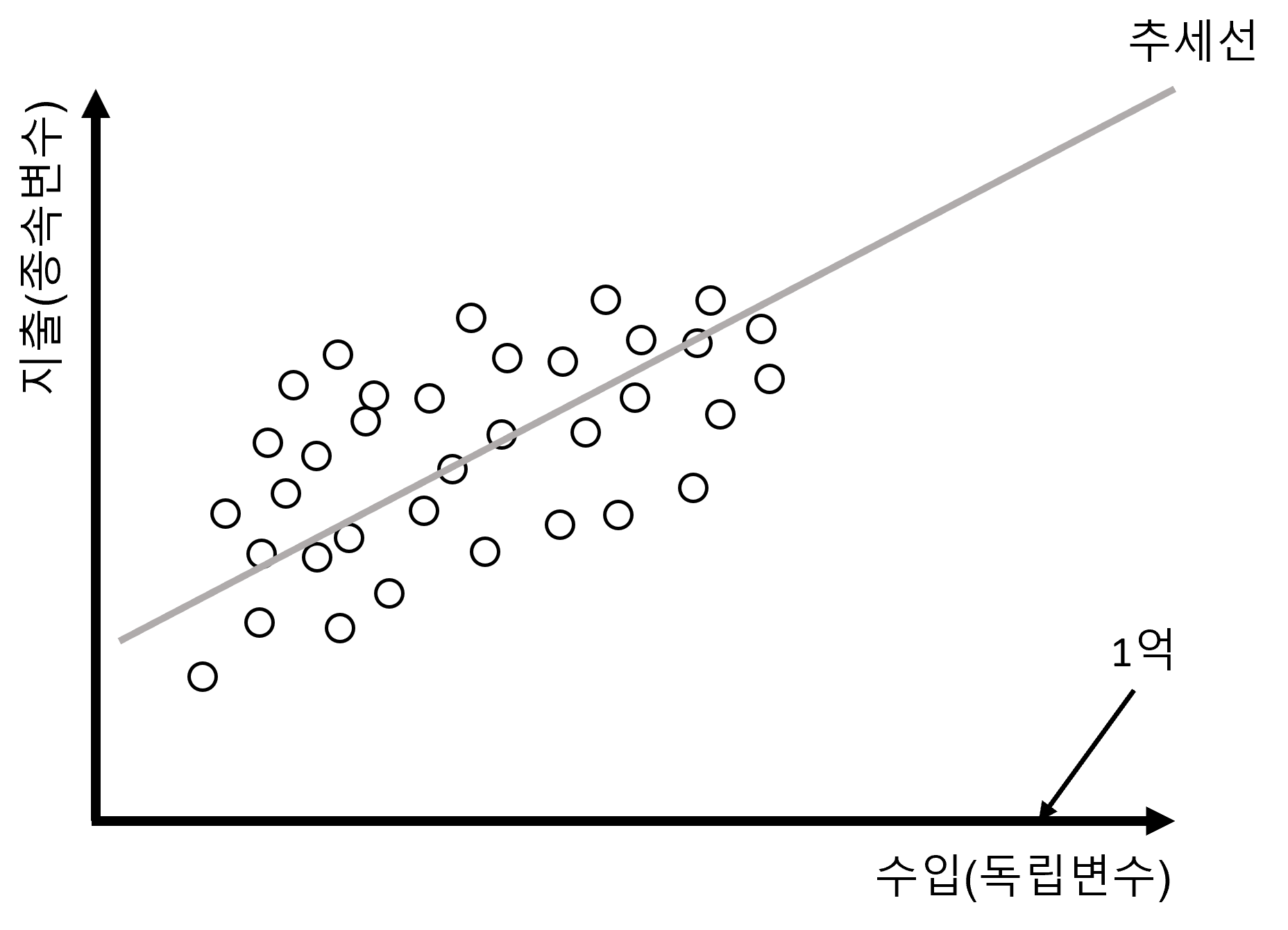
고전적인 경제학에서 다루던 예제입니다. 우리는 지금 개인의 수입과 지출 금액에 대한 정보를 데이터로 가지고 있습니다. 기본적인 가설은 개인의 수입이 많아질 수록 지출이 늘어날 것이라는 것이 우리의 가설입니다. 당연히 수입이 있어야 지출이 가능하기 때문에 이런 가설은 논리적으로 크게 문제가 없어 보입니다. 즉, 수입이 많은 사람이 지출도 많을 것이기 때문입니다. 그래서 우리가 가진 데이터를 다음과 같이 그래프로 그려보았습니다.

Figure 2.1 (a) 에서 보면 수입을 독립변수로 하여 X축에 지출을 종속변수로 하여 Y축에 두었습니다. 항상 지켜야할 약속은 독립변수는 X축에 종속변수는 Y축에 두는 것입니다. 이를 바꿔서 그리겠다고 하면 문제가 됩니다. 이러한 것은 일종의 약속이기 때문입니다. Figure 2.1 (a) 을 보니 우리가 가진 데이터가 우상향하는 경향이 있음을 알 수 있습니다. 그런데, 만약 우리가 궁금한 것이 만약 수입이 1억원이라면 지출이 얼마 정도 될지 알고 싶다고 가정합니다(Figure 2.1 (b)). 그럼 위의 데이터를 보면서 우리는 어떤 생각을 떠 올리게 될까요?

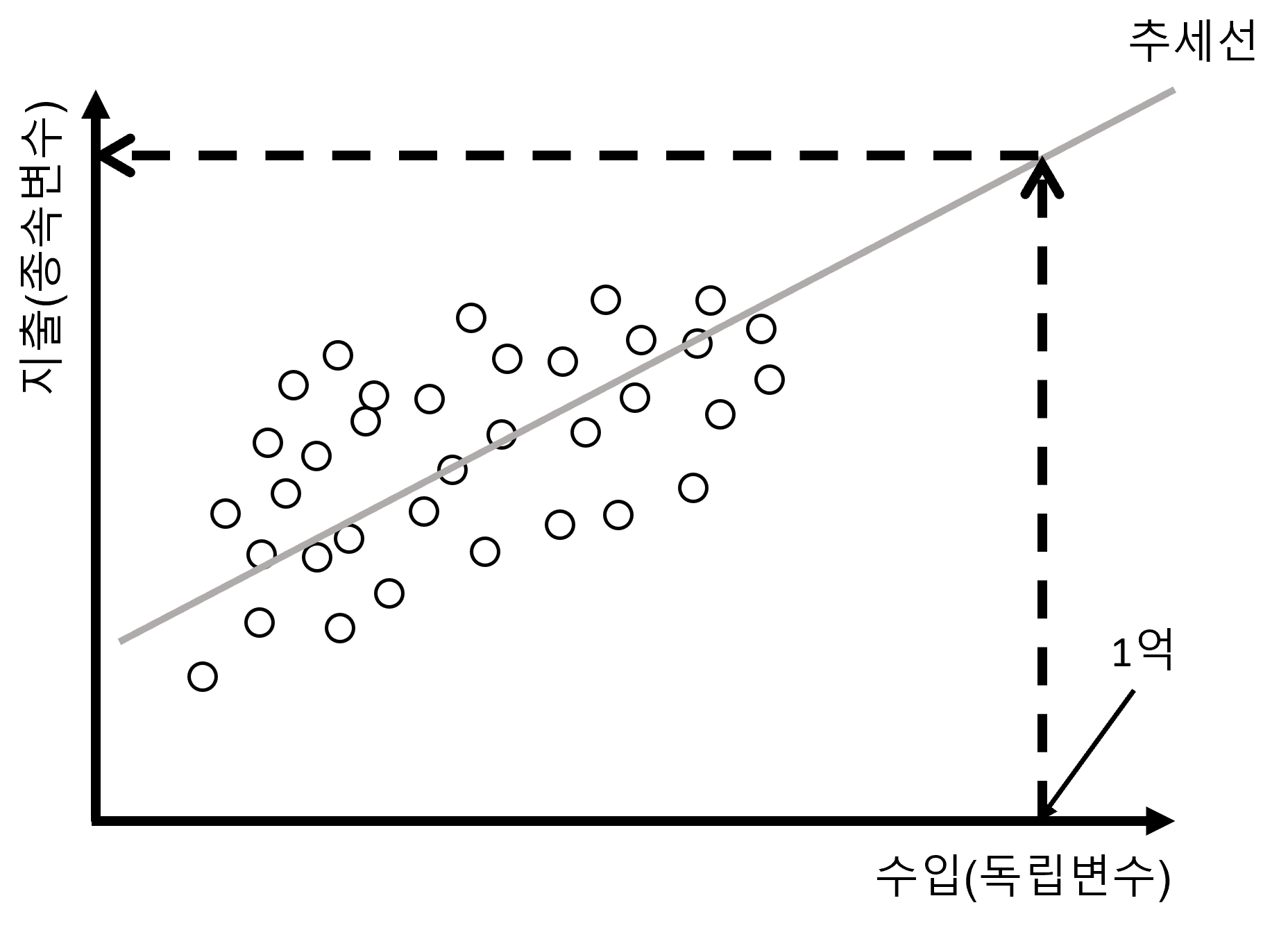
아마도 우리는 자연스럽게 우상향하는 데이터를 보면서 이 데이터를 대표할 수 있을 만한 직선 하나를 긋고 싶어하게 될 것입니다. 우리는 이 직선을 추세선(Figure 2.2 (a))이라고 부릅니다. 만약 우리가 충분히 믿을만한(?) 혹은 우리의 데이터를 가장 잘 대표할 수 있을 만한 추세선을 알 수만 있다면 이 추세선을 이용하여 Figure 2.2 (b) 에서 볼 수 있듯이 1억원의 수입에 대응하는 추세선의 값을 찾아서 지출을 예측할 수 있을 것입니다. 우리가 가진 데이터에서 수입이 1억원이 되는 실제 값이 없더라도 이 추세선을 이용한다면 충분히 수입이 1억원 정도 되는 사람이 얼마나 지출을 할지 예측할 수 있을 것입니다.

결론적으로 회귀분석을 한다는 것은 회귀분석을 통해 이 추세선을 찾아내는 것이라고 할 수 있습니다. 회귀분석의 결과를 이용하면 우리는 이러한 추세선을 그릴 수 있기 때문입니다. 그렇다면 이제 이 추세선에 대해 좀 더 자세히 알아 봅시다.

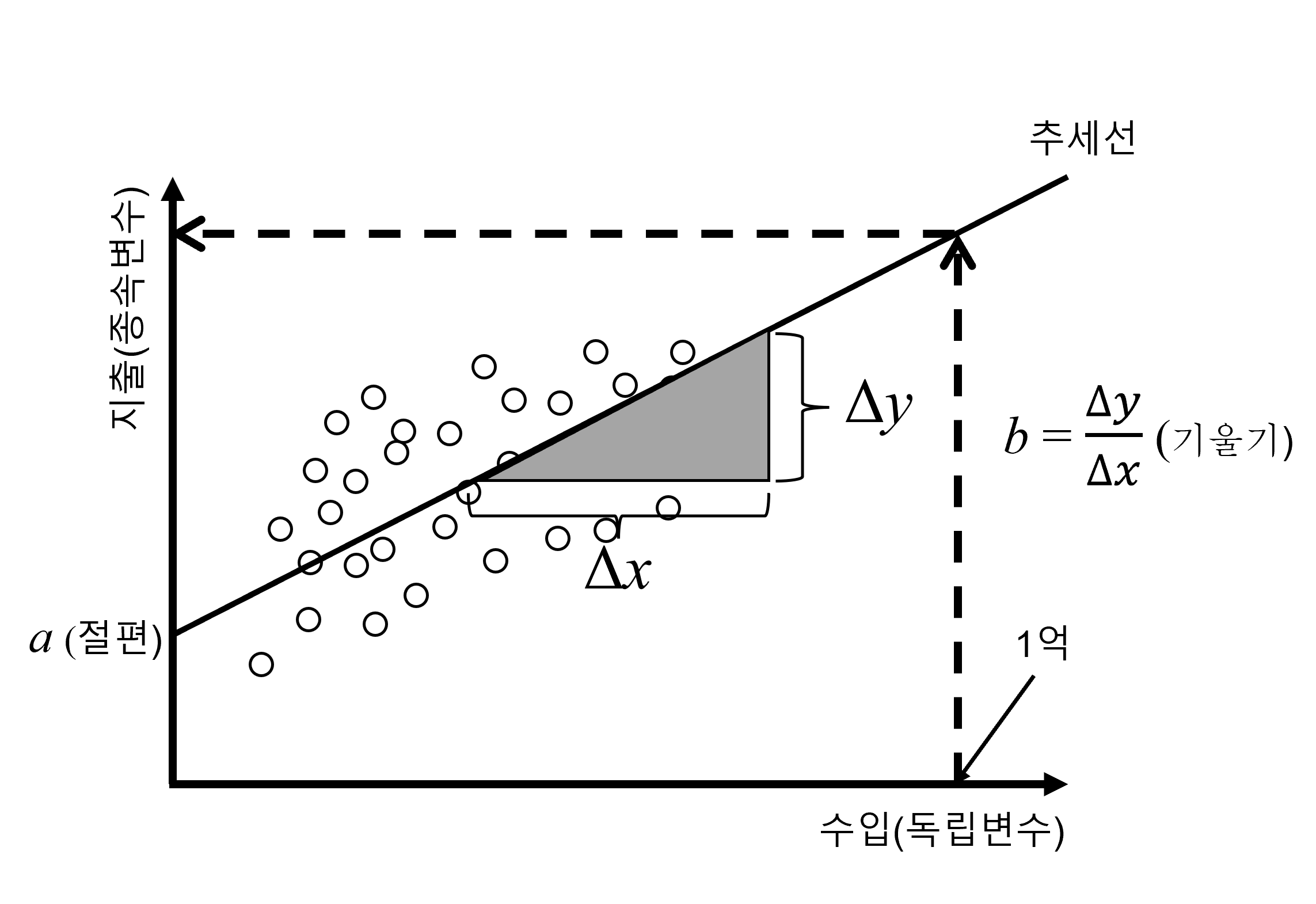
Figure 2.3 에서 보는 것 처럼 추세선은 결국 2차원 평면상의 직선이고, 이는 우리가 중학교 때 배운 직선의 방정식을 이용해 간단하게 표현할 수 있습니다. 추세선의 직선의 방정식은 다음과 같습니다.

\[\hat{y} = a + b\bar{x}\]

여기서 일반적으로 사용되는 $x$, $y$ 대신에 $\bar{x}$를 쓴 이유는 앞서 이야기 했듯이 회귀분석은 결국 평균값을 지나가는 것이기 때문입니다. 새로운 것이 바로 $\hat{y}$인데, $y$위에 붙은 것을 모자 즉 hat이라고 부릅니다. 그래서 이를 읽을 때는 y hat이라고 읽습니다. 굳이 $y$가 아니라 $\hat{y}$이라고 하는 이유는 이 둘을 구분해야 하기 때문입니다. 여기서 $y$는 애초에 우리가 가지고 시작한 데이터의 변수인 $y$입니다. 사실 정확하게 말하자면 $y_i$라고 해야할 것입니다. 왜냐하면 데이터의 사이즈 즉 관찰값의 개수에 따라 $i$는 1부터 $n$까지 있기 때문입니다. 그러므로 위의 식에서 말하는 $\hat{y}$이란 데이터를 이용해 구해낸 추세선을 의미합니다. 사실 이 추세선을 회귀분석에서는 회귀식이라고 부르고 $\hat{y}$은 회귀분석을 통해 예측된 일종의 예측값이 됩니다.

그러나, 우리의 관심사는 사실 $\bar{x}$도 $\hat{y}$도 아닙니다. 위의 추세선 즉 회귀식에서 중요한 것은 $a$와 $b$입니다. $a$와 $b$에 대해서 우리는 이미 중학교 때 배운 바 있습니다. 그러나 한 번 더 기억을 되새겨 보면, $a$는 절편이라고 부릅니다. 영어로는 constant라고 하기도 합니다. $b$는 기울기라고 부르고 영어로는 slope 라고 합니다. 중요한 특성을 이야기 하자면 $x$가 0이 될 때 $\hat{y} = a$가 됩니다. 그러므로 Figure 2.3 에서 보듯 절편 $a$는 y축과 회귀식(회귀직선)이 만나는 점이 됩니다. 좀 더 엄밀한 의미로 보면 $\hat{y} = a$는 $y$값의 평균이 $a$라는 의미입니다. 왜냐하면 회귀분석은 평균으로의 회귀인데 $\hat{y} = a$에서는 $x$가 없으므로 이 식은 $y$값의 평균을 의미합니다.

Figure 2.3 를 보면 기울기 $b$를 다음과 같이 표현합니다.

\[b = \frac{\Delta{y}}{\Delta{x}}\]

여기서 $\Delta$란 델타라고 읽고 두 값의 차이 혹은 증가분을 의미합니다. 따라서 기울기 $b$는 $x$값의 증가분 분의 $y$값의 증가분입니다. 이해를 쉽게 하기 위해 위의 기울기의 식에서 분모의 $\Delta{x} = 1$로 제한을 하면, 기울기 $b$란 $x$가 1 증가할 때 $y$값의 증가분이 됩니다. 다른 말로, $x$가 1 증가할 때 $y$값이 얼마나 증가했는지를 의미하는 것입니다. 만약 이 기울기가 크다면 회귀직선이 가파르게 증가하는 모양일 것이고, 이 기울기가 작다면 회귀직선이 매우 완만하게 증가하는 모양일 것입니다. 물론 이것은 기울기 $b$가 양수일 경우이고, 반대로 기울기 $b$가 음수라면 기울기가 커질 수록 회귀직선은 가파르게 감소하고 작을 수록 완만하게 감소한다는 의미가 됩니다.

그렇다면 이제 Figure 2.3 의 데이터값 즉 점들은 어떻게 표현해야 할까요?

\[y_i = a + bx_i + e_i\]

위의 식에서 $e_i$란 오차를 의미합니다. 왜냐하면 $a$와 $b$는 회귀식에서 나온 것이므로 당연히 어떤 값 $x_i$를 이 회귀식에 넣어도 정확하게 $y_i$가 나오지 않을 것입니다. 이때 예측된 회귀직선의 식과 실제 관찰된 값의 차이가 오차 $e_i$가 되는 것이고, 오차는 모든 값에 따라 다 다르게 됩니다. 그렇다면 이제 우리는 이 오차에 조금 더 관심을 가져보도록 하겠습니다.

Figure 2.3 를 데이터 부분만 확대해서 살펴보면 아래와 같습니다.

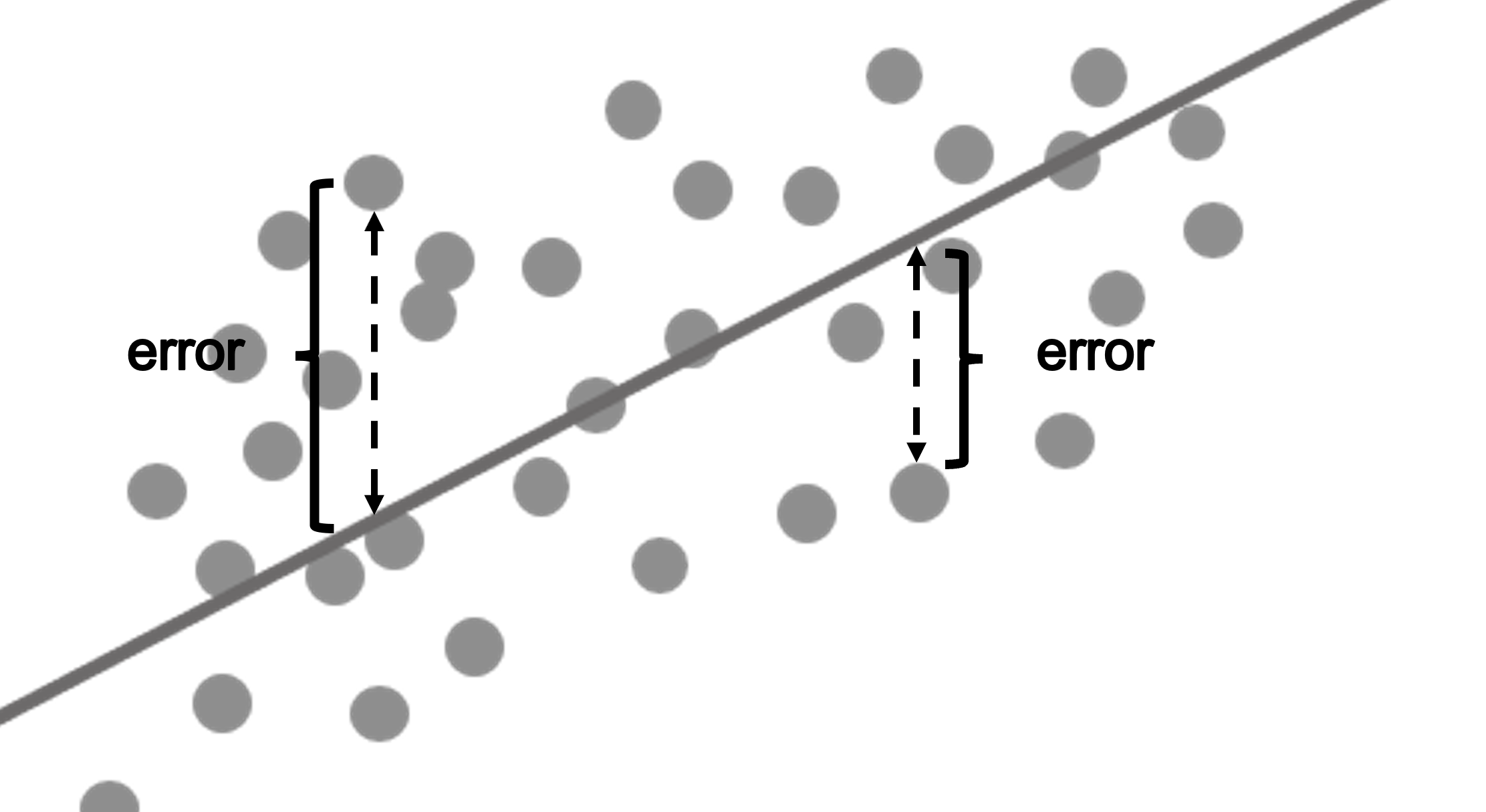
위에서 설명했듯이 오차는 필연적으로 발생합니다. 혹시라도 오차가 전혀 없는 분석방법을 기대하셨다면 그건 어디까지나 판타지일 것입니다. 오차는 발생하기 마련이고 이 오차를 우리가 얼마나 잘 이용하느냐가 바로 통계의 핵심이기도 합니다. 위의 오차는 다음과 같이 표현될 수 있습니다.

\[e_i = y_i - \hat{y_i}\]

즉, 오차란 측정값(혹은 관찰값)에서 예측값을 뺀 것입니다. 여기서 예측값이란 회귀분석을 통해 예측된 값을 의미합니다. 그렇다면 Figure 2.4 을 보면서 가장 합리적인 추세선이란 무엇일까 생각해 봅시다. 오차를 자세히 살펴보면 결론적으로 오차가 가장 작은 추세선이 가장 합리적인 추세선일 것입니다. 또한 이 추세선이 가장 데이터를 잘 표현하는 혹은 대표하는 추세선이 될 것입니다. 따라서 우리는 오차의 합이 가장 작은 추세선을 가장 합리적인 추세선으로 보고 이 추세선이 회귀직선이 되도록 하는 것이 가장 최선의 선택일 것입니다.

문제는 이 오차가 양수(+)도 있고 음수(-)도 있다는 사실입니다. Figure 2.4 의 좌측편은 양수가 되는 오차이고 우측은 음수가 되는 오차입니다. 이렇게 음수와 양수의오차가 혼재되어 있을 경우 그냥 더하면 엉망진창이 될 것입니다. 어떻게 하면 될까요?

맞습니다. 모든 오차를 제곱하여 합하면 됩니다.

그러므로, 가장 합리적인 추세선이란 오차의 제곱의 합이 최소화된 직선일 것입니다. 우리는 이 방법을 수학적으로 최소제곱법이라고 합니다. 즉 앞에서 본 회귀직선의 방정식에서 우리가 필요로 하는 $a$와 $b$는 최소제곱법이라는 수학적 방법으로 구해집니다.

그러데, 이 표현이 어디서 많이 본 것 같지 않나요? 사실 가만히 생각해보면 왜 회귀분석이 즉 회귀직선이 평균을 지나가야 하는지 이해가 됩니다. 사실 최소제곱법이라는 수학적인 방법을 우리가 여기서 공부할 필요는 없습니다. 수학과 혹은 통계학과 전공자라면 알아야 하겠지만 우리는 이해만 하면 됩니다. 오차의 제곱의 합이 최소가 된다는 것은 결국 계산상 분산의 분자부분의 계산방법과 매우 유사하고 이 부분이 최소가 되려면 결국 평균값을 지나가는 것이 최선이라는 의미가 됩니다. 그러므로 우리의 데이터를 가장 잘 나타내는 합리적인 직선인 회귀직선은 평균을 지나가는 그리고 오차의 제곱의 합이 최소가 되는 직선이 된다는 것입니다. 일반적으로 이러한 회귀분석의 방법을 영어로는 기본적으로 OLS (Ordinary Least Square)라고 합니다.

이제 회귀분석의 기초적인 내용을 이해했습니다. 조금씩 더 앞으로 나가보도록 합시다.

Youtube 바로 가기

2.2 결과표를 해석하자

앞서 공부한 다른 방법들은 계산하는 법이라던가 기본적인 체계를 먼저 이해하고 분석결과를 해석하는 순서로 진행했지만, 제가 수 년간 가르쳐본 결과 회귀분석은 순서를 바꾸는 것이 더 효과적이라는 것을 알게 되었습니다. 그래서 회귀분석의 기본을 이해했다면 바로 회귀분석의 결과표를 해석해보도록 하겠습니다. 다소 의아스러울 수 있겠지만 믿고 따라와 주길 바랍니다.

2.2.1 회귀분석의 예제 데이터와 연구가설

먼저 우리가 분석할 데이터와 회귀분석으로 우리가 기대하는 나름의 연구가설을 설명하겠습니다.

데이터와 변수
- Data: House sales price in Kings County, USA (다운로드)
- 종속변수: price (매매가격)
- 독립변수: sqft_living (거실크기-단위:$feet^2$)
연구가설
- 거실의 크기가 클 수록 매매 가격이 비쌀 것이다.
- 논리적 배경: 거실의 크기가 크다는 것은 일반적으로 집의 규모가 크다는 의미일 것이기 때문에
인과관계의 예측:
- 독립변수가 종속변수에 정(+)의 영향을 미칠 것이다
- 원인: 거실의 크기
- 결과: 매매 가격

사실 연구가설이라고 하기에는 사회과학적 측면에서 보자면 이론이 없고 논리가 다소 빈약해 보이는 것이 사실입니다. 여기에 너무 집착하지 말고 일단 회귀분석 결과표를 이해하고 해석하는 것에 주안점을 두고 보도록 합시다.

2.2.2 회귀분석 결과표의 해석

Figure 2.5 의 좌측이 Jamovi 결과이고 우측이 SPSS 결과입니다. 결과 자체가 다르지 않고 소수점의 자리수 차이만 있습니다. 요즘은 그런 분들이 거의 없긴 합니다만, 가끔 SPSS 아니면 안된다는 분들이 있습니다. 혹은 다른 통계 프로그램은 틀렸다거나 결과가 다르다거나 이런 이야기 하시는데, 참으로 안타까울 뿐입니다.

이제 Jamovi의 결과표를 이용해서 하나씩 설명하겠습니다.

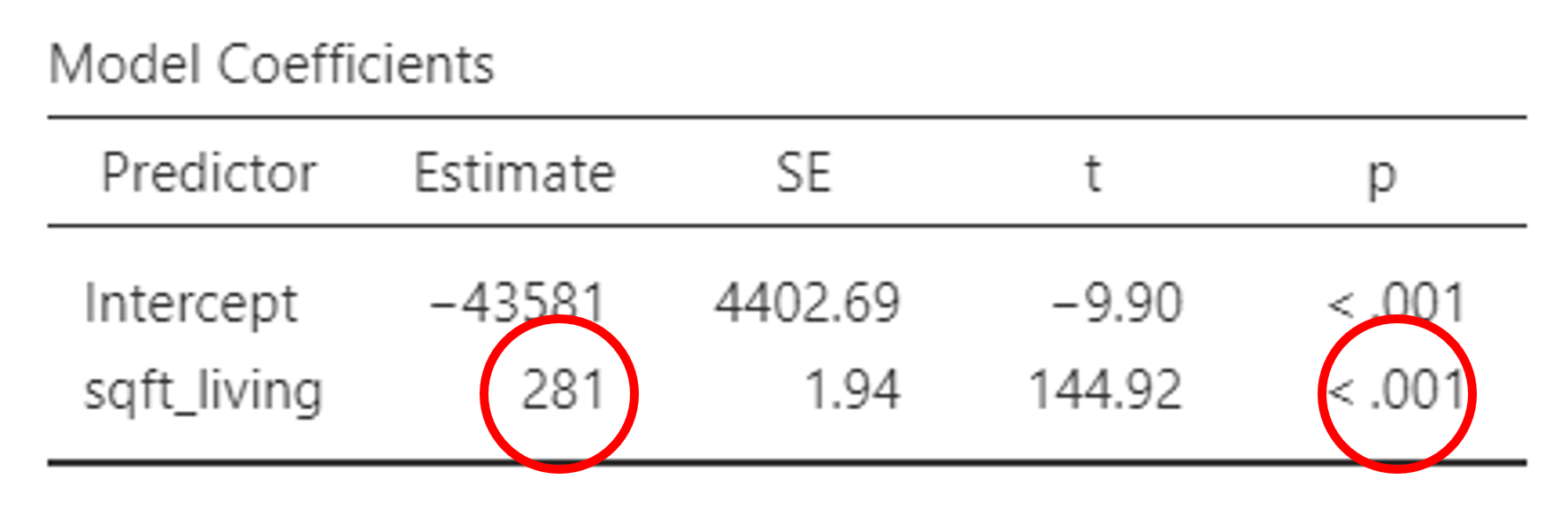
첫번째 열에 있는 것은 Predictor라고 되어 있습니다. 독립변수를 Independent variable이라는 말 대신 Predictor라고도 합니다. 예측변수라고 할 수 있겠습니다. 그 아래에 독립변수의 변수명이 있습니다. 첫번째가 Intercept라고 되어 있는데 이는 영어로 상수라는 말인데 Constant와 같은 말입니다. 즉 회귀식의 상수라는 의미입니다. 그 아래에 sqft_living 이라는 독립변수의 변수명이 표시되어 있습니다.

두번째 열에는 Estimate라고 되어 있는데 어떤 프로그램에서는 Coefficient 라고 되어 있기도 합니다. 회귀계수입니다. 회귀계수란 우리가 앞서 공부한 회귀식의 $a$와 $b$를 말합니다. 즉, 최소제곱법에 의해 수학적으로 계산된 회귀계수입니다. 위의 회귀계수를 이용해 회귀식을 다시 써보면 다음과 같습니다.

\[\hat{y} = a + b\bar{x} = -43581 + 281\bar{x}\]

즉 절편(상수)이 -43581이고 기울기가 281이라는 의미입니다. 사실 위의 회귀분석 결과표에서 우리의 관심사는 기울기 281입니다. 왜냐하면 독립변수 sqft_living이 종속변수 price에 미치는 영향은 기울기 $b$인 281로 나타나기 때문입니다. 여기서 한 가지 중요한 사실은 회귀계수 중 기울기 281은 수학적 계산방법인 최소제곱법에 의해 계산된 숫자일 뿐 아직은 전혀 통계적인 의사결정을 할 수 없는 상황이라는 점입니다. 이게 무슨 뜻인지 잘 이해가 되시지 않겠지만 일단은 이정도만 이해하고 뒤에서 좀 더 자세하게 다루겠습니다.

세번째 열의 SE는 Standard Error로 표준오차입니다. 표준오차는 표준편차와 비슷하지만 개념이 좀 다릅니다. 복잡한 이야기는 뒤에서 하기로 하고 일단 여기서는 이런게 있다는 것만 이해하고 넘어가도록 하겠습니다.

네번째 열의 t는 t-value입니다. 갑자기 회귀분석에 왜 t-value가 등장하냐고 생각하실 수 있겠으나, 본질적으로 회귀분석의 각 변수의 유의성을 확인하는 통계적인 방법은 t-test입니다. 그래서 t-value가 나오는 것입니다. 이 부분도 뒤에서 좀 더 자세하게 다루겠습니다.

마지막 열의 p는 당연히 p-value 즉 p값입니다. 이 p값은 각 변수 여기서는 절편인 intercept와 독립변수인 sqft_living이 유의한지 아닌지 알려주는 p-value입니다. 당연히 5%보다 작으면 유의하고 5%보다 크면 유의하지 않습니다. 계속 이야기 하지만 우리의 관심사는 독립변수 sqft_living이 유의한지 아닌지입니다. 보다 정확하게 말하자면 독립변수의 회귀계수인 기울기 281이 통계적으로 유의한지 아닌지를 여기서의 p-value가 알려주는 것입니다. 위의 결과표를 보면 독립변수 sqft_living 의 p-value는 <.001 이라고 되어 있고 이는 p-value가 0.001보다 작다는 의미이므로 매우 유의한 결과를 보이고 있습니다.

이제 이 회귀분석의 결과표와 그래프를 연결해서 이해해 보도록 합시다.

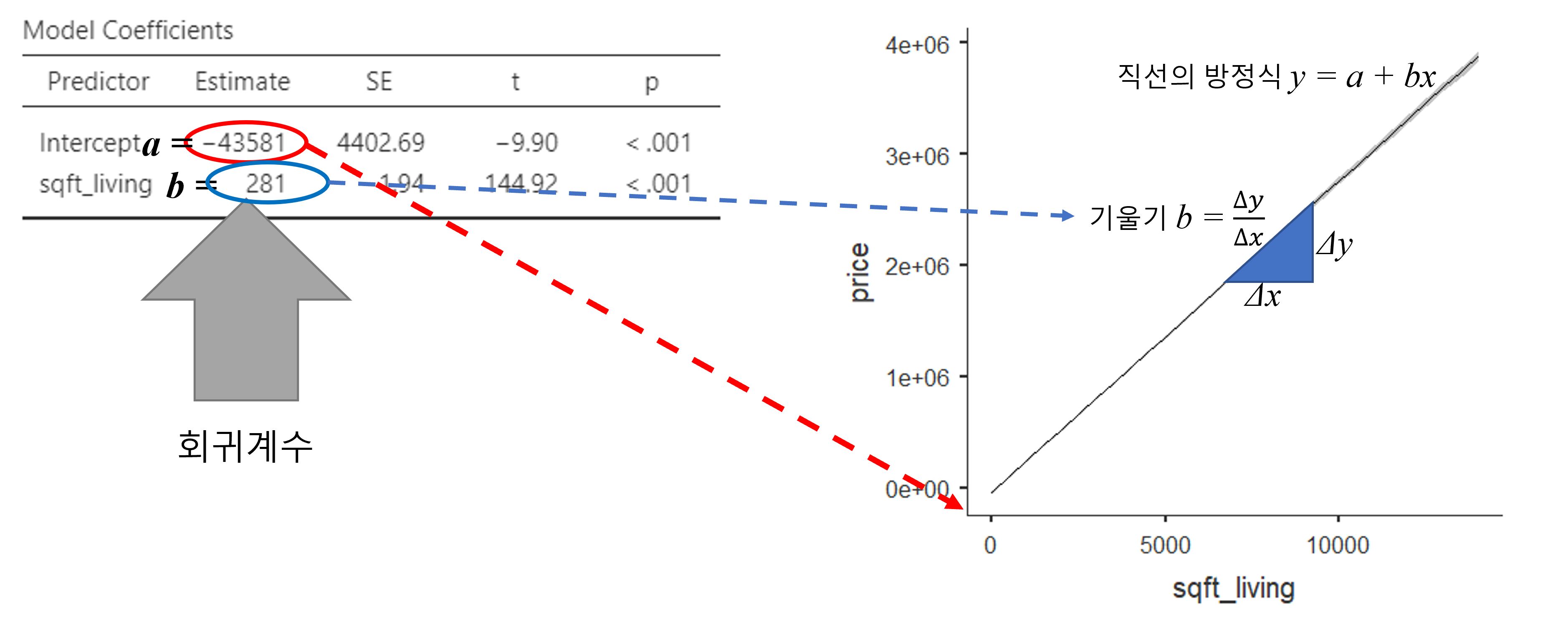
\[\hat{y} = a + b\bar{x} = -43581 + 281\bar{x}\]

회귀분석 결과를 그래프로 그린 것이 Figure 2.7 의 우측 그래프입니다. 회귀식의 절편 -43581은 원래 회귀직선과 y축이 만나는 점인데, 그림상 y축의 아랫부분이 좀 생략이 되어 있어 잘 보이지는 않습니다만 그림의 붉은 점선이 가리키는 부분입니다. 사실 앞서 이야기 했듯이 이 절편은 종속변수 y의 평균값을 의미합니다. 여기서는 price라는 주택매매 가격의 평균인데 값이 좀 이상합니다. 음수가 나왔다는 것은 사실상 말도 안되는 것입니다. 이유는 간단합니다. 우리가 너무 단순한 회귀식을 사용하여 분석했기 때문에 현실을 제대로 반영하지 못한 것입니다. 혹은 우리의 회귀식 자체가 좀 문제가 있다는 의미이기도 합니다. 여기서는 단순화된 예제를 사용해 회귀분석 결과표를 이해하는 것이 목적이므로 이에 대해 깊게 이야기 하지는 않겠습니다.

중요한 것은 바로 파란색 점선입니다. 회귀식의 기울기 $b$가 281이고 이 기울기가 우측의 그래프에서 우상향하는 모습으로 표현되어 있습니다. 제가 굳이 이렇게 회귀분석 결과와 그래프를 연결해서 보여주는 이유는 회귀분석에 대한 이해를 돕기 위함입니다. 무엇이든지 머릿속에서 이 그래프를 그릴 수 있다면 이해의 정도와 속도가 매우 깊고 빨라지기 때문입니다.

다시 한 번 강조하지만, 우리가 회귀분석을 한다는 것은 위와 같은 회귀직선의 방정식을 얻는 것이고 이 방정식에서 두 개의 회귀계수(절편과 기울기)를 알아 내는 것이 최종적인 목적입니다. 더불어 이 두 회귀계수 중에서 기울기가 통계적으로 유의한지 확인하는 것이 최종적인 목적이 됩니다. 우리의 연구가설은 거실의 크기가 클 수록 매매가격이 비싸질 것이라는 것입니다. 결과적으로 우리의 회귀분석 결과표는 이러한 연구가설이 옳다는 것을 보여주었습니다.

문제는 대부분의 경우 “유의하다”라는 말만 하고 끝난다는 것입니다.

제가 학생들을 가르치면서 계속 강조하는 것이 바로 이 유의하다라는 말에서 끝나서는 안된다는 것입니다. 결과를 다시 한 번 살펴보면,

\[\hat{y} = a + b\bar{x} = -43581 + 281\bar{x}\]

이 회귀직선에서 기울기 281은 통계적으로 유의하였고, 이 값이 의미하는 바는 거실의 크기가 1$feet^2$ 증가할 때, 주택의 매매가격이 평균적으로 281 US dollar 증가한다는 것입니다. 이렇게 보다 자세하고 정확하게 의미를 짚어서 해석하는 것이 진정한 회귀분석의 목적입니다. 그러니 유의하다라는 것에 집착하고 거기서 끝내지 말기 바랍니다.

Youtube 바로 가기

2.3 회귀분석과 표준오차

2.3.1 표준오차란 무엇일까?

이번에는 회귀분석과 표준오차에 대해 알아보겠습니다. 앞 시간에 표준오차는 jamovi의 결과표에서 SE라는 것으로 표현되었습니다. 여기서 SE란 Standard Error의 약자입니다. 그렇다면 이 표준오차가 무엇을 의미하는 것일까요? 여러분들이 통계 교과서를 찾아보거나 인터넷을 검색해 보면 뭔가 알듯 말듯한 말로 표현되어 있을 것입니다. 계속 이야기 하지만, 여러분들이 통계전공을 할 것이 아니라면 일단 이런 복잡한 설명은 잠시 접어두고, 그림으로 이해해 보는 것이 보다 좋을 것 같습니다. 아래의 그림을 한 번 살펴봅시다.

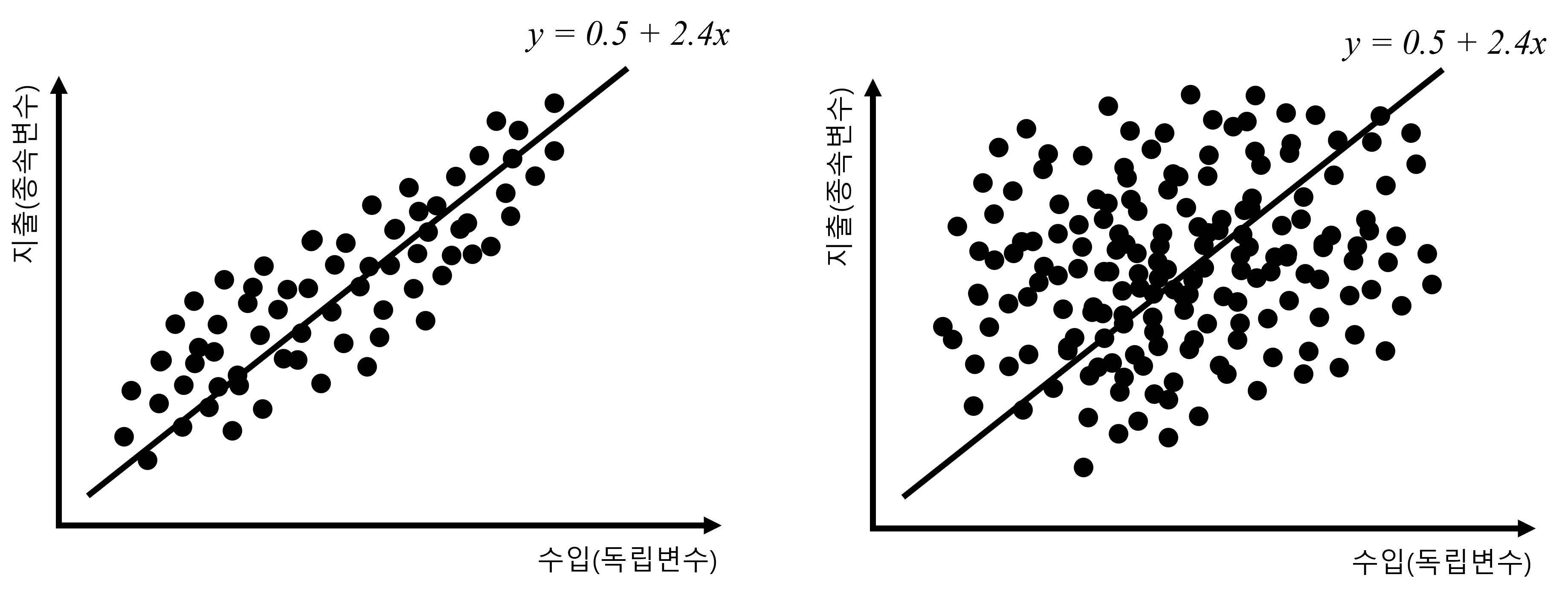
우리가 두 개의 데이터를 가지고 있고, 이 두 개의 데이터로 간단한 회귀분석을 진행했다고 가정합니다. 그리고나서 우리는 두 개의 데이터의 회귀분석 결과를 위와 같이 그림으로 표현하였습니다.

위의 결과그래프 우측 상단에 각각의 최종적인 회귀식이 표현되어 있습니다. 공교롭게도 두 데이터의 회귀분석 결과 회귀식은 동일하게 나타났습니다.

\[ y = 0.5 + 2.4x\]

무슨 뜻일까요? $x$가 1 증가할 때, $y$는 2.4 증가한다는 의미입니다. 그렇다면 다시 위의 그림을 살펴봅시다. 회귀식은 동일하지만, 데이터가 상당히 차이가 있어보입니다. 좌측의 데이터는 회귀식을 중심으로 데이터의 점들이 촘촘하게 잘 모여있는 것으로 보이지민, 우측의 데이터는 회귀식을 중심으로 데이터의 점들이 넓게 퍼져있습니다.

이제 여기서부터 본격적인 회귀분석의 통계가 시작됩니다. 앞에서도 이야기 했지만, 위의 회귀분석식의 회귀계수는 최소제곱법에 의해 수리적으로 계산되어 나온 것이므로 이는 수학적 해(결과)입니다. 위의 두 데이터를 이용한 회귀분석의 결과 $x$가 1 증가할 때, $y$는 2.4 증가한다는 것을 우리는 알았습니다. 문제는 두 데이터가 분명히 차이가 있어 보인다는 것이지요.

이제 우리는 다시 우리가 이 공부를 시작한 제일 처음으로 돌아가야 합니다.

처음 통계를 이야기 할 때, 제가 한 말이 기억이 나시나요? 통계적 사고방식이란 무엇이라고 했나요? 기억이 나지 않으시는 분들을 위해 간단하게 말하자면, 통계란 이 사건이 우연히 발생하지 않았을까? 라는 질문에서 시작한다고 이야기 했습니다. 회귀방정식의 결과를 봤을 때, $x$가 1 증가할 때, $y$는 2.4 증가한다고 하는데, 이 2.4의 증가가 우연히 발생하지는 않았을까? 라고 질문하는 것이 바로 통계의 시작이라는 것입니다.

아마도, 통계에 익숙하지 않은 분들이라면 이 말 자체가 이해가 되지 않을 것입니다. 여기서 우리는 수학적 해(답)와 통계적 의사결정은 다르다는 것을 이해해야 합니다. 수학적으로는 최소제곱법이 오차의 제곱 합이 최소가 되는 회귀방정식을 구해줄뿐, 이 회귀식의 회귀계수가 우연인지 아닌지 (유의한지 아닌지) 알려주지 않는다는 것이 핵심입니다.

그렇다면, 우리는 회귀계수 2.4가 우연인지 아닌지 혹은 유의한지 아닌지 어떻게 판단해야 할까요?

앞의 내용을 충실히 이해하고 여기까지 오신 분들이라면 아마도 비교대상이 필요하다는 것을 눈치 채셨을 겁니다.

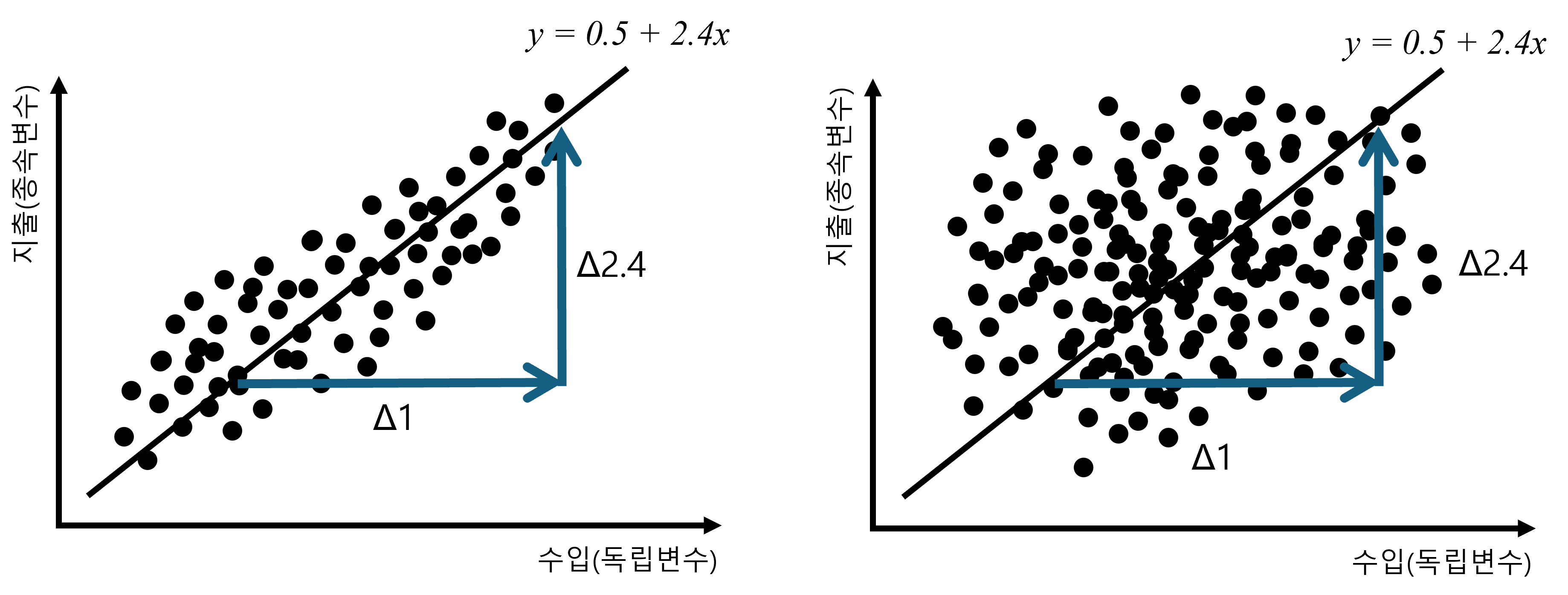
Figure 2.9 을 보시면 둘 다 분명히 $x$가 1 증가할 때, $y$는 2.4 증가한다는 것을 알 수 있습니다. 문제는 확률적으로 누가 더 $x$가 1 증가할 때, $y$는 2.4 증가할까? 라는 것이지요. 직관적으로 봐도 좌측의 경우가 우측보다는 $x$가 1 증가할 때, $y$는 2.4 증가할 가능성(확률)이 높아 보입니다.

2.3.2 표준오차의 정의

여기서 표준오차에 대해 보다 자세히 알아보겠습니다. 통계책을 살펴보면, 표준오차란? - 우리는 무엇을 하든지 대부분 모집단이 아닌 표본으로 통계분석을 하게 되는데, - 우리는 우리가 가진 표본이 얼마나 모집단에 가까운지 아닌지를 판단해야 합니다. - 즉, 모집단의 평균을 평균의 참값이라고 보고, - 표본의 평균값이 모집단의 평균값과 얼마나 가까운지 혹은 멀리 있는지를 계산하게 되는데, - 이론적으로는 같은 모집단에서 적합한 방법으로 표본을 뽑아도 표본의 평균값은 매번 조금씩 다를 수 밖에 없습니다. - 그러므로, 여러번 표본을 뽑아서 표본들의 평균값을 구하고, 이를 이용해 표본들의 평균값의 표준편차를 구합니다. - 이때, 이 표준편차를 표준오차라고 부르는데, - 이 표준오차가 작으면 표본의 평균값이 모집단의 평균값인 참값에 더 가깝다는 것이고, 표준오차가 크면 이 참값에서 더 멀다는 뜻이 됩니다.

결론적으로 표준오차가 크다는 것은 표본의 평균값이 참값으로부터 멀어져 있다고 보는 것이지요. 그렇다면 이 개념을 위의 그림에 다시 대입해 보면 이렇게 볼 수 있습니다.

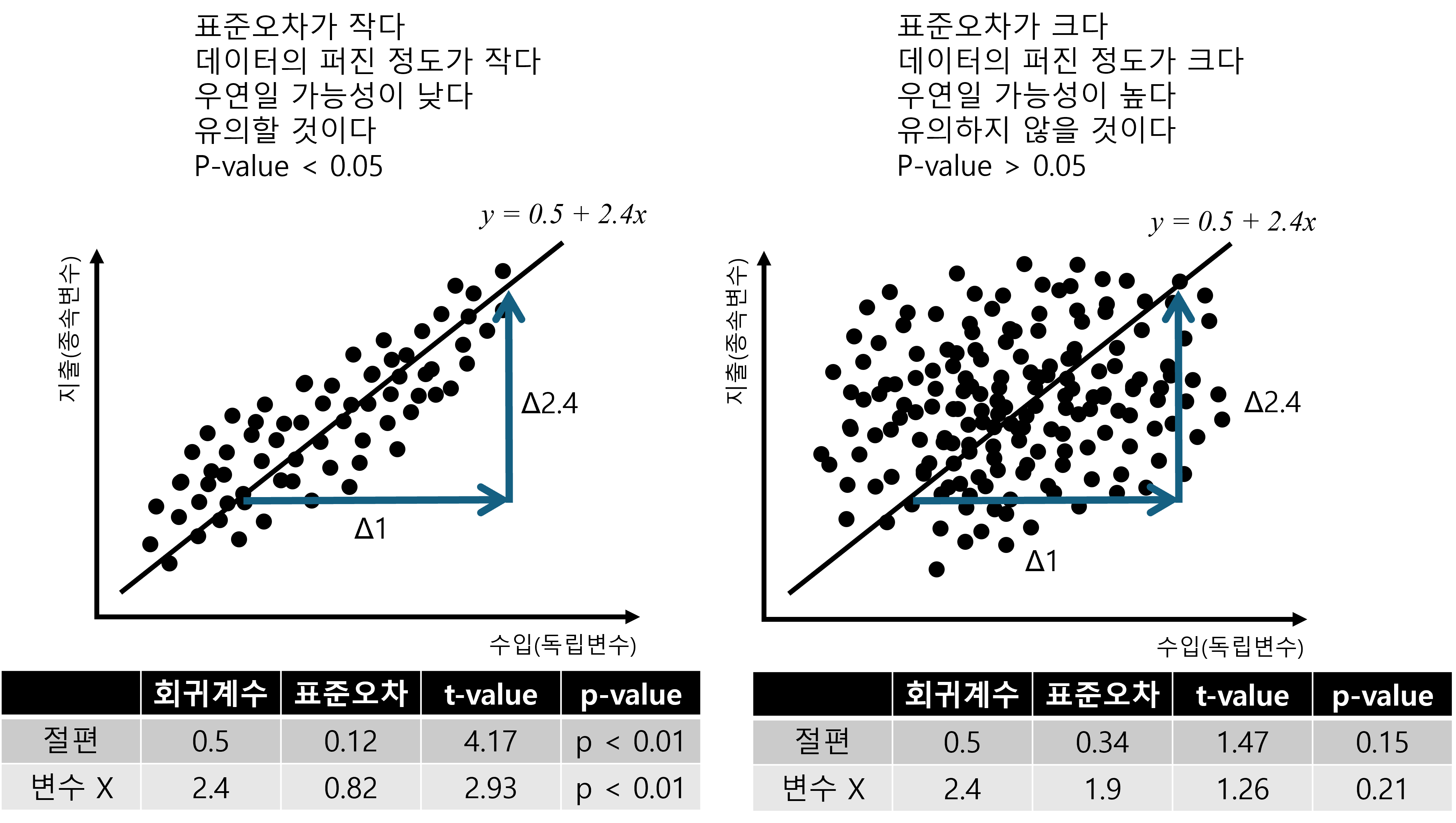
Figure 2.10 의 그림과 회귀분석 결과표를 비교해 보면, 좌측의 경우 변수 $x$의 표준오차가 0.82인 반면, 우측의 경우 변수 $x$의 표준오차가 1.9로 거의 두 배인 것을 볼 수 있습니다. 즉 표준오차가 크므로 회귀계수 2.4가 유의할 가능성이 좌측은 높지만 우측은 낮다고 볼 수 있습니다. 물론 정확한 것은 p-value를 보아야 하지만 말입니다.

정리해 보면 다음과 같습니다.

회귀계수는 최소제곱법으로 구해진다
- 그러나 그렇게 계산된 회귀계수가 우연인지 아닌지는 모른다
- 그래서 이 회귀계수가 우연일 확률을 알기 위해 표준오차를 사용한다
표준오차가 작으면 회귀계수가 우연일 확률이 낮다
- 표준오차가 작다는 것은 데이터가 회귀직선에 가까이 모여 있다는 의미이고,
표준오차가 크면 회귀계수가 우연일 확률이 높다
- 표준오차가 크다는 것은 데이터가 회귀직선에서 멀리 퍼져있다는 의미이다
그렇다면 이 확률(p-value)을 어떻게 계산할까?
- 정답은 t-test

그렇다면 이제 회귀분석에서 t-test를 공부해보도록 합시다.

Youtube 바로 가기

2.4 회귀분석과 t-test

2.4.1 왜 t-test일까?

지난 시간에 공부한 내용을 정리해보면 다음과 같습니다.

회귀계수는 최소제곱법으로 구해진다
- 그러나, 그렇게 계산된 회귀계수가 우연인지 아닌지는 모른다
- 그래서 이 회귀계수가 우연일 확률을 알기 위해 표준오차를 사용한다
표준오차가 작으면 회귀계수가 우연일 확률이 낮다
- 표준오차가 작다는 것은 데이터가 회귀직선에 가까이 퍼져있다는 의미이고,
표준오차가 크면 회귀계수가 우연일 확률이 크다
- 표준오차가 크다는 것은 데이터가 회귀직선에서 멀리 퍼져있다는 의미인데,
그렇다면 이 확률을 어떻게 계산할까?
- 바로 t-test를 이용한다

이렇게 됩니다.

앞의 두 경우를 다시 한 번 살펴보면,

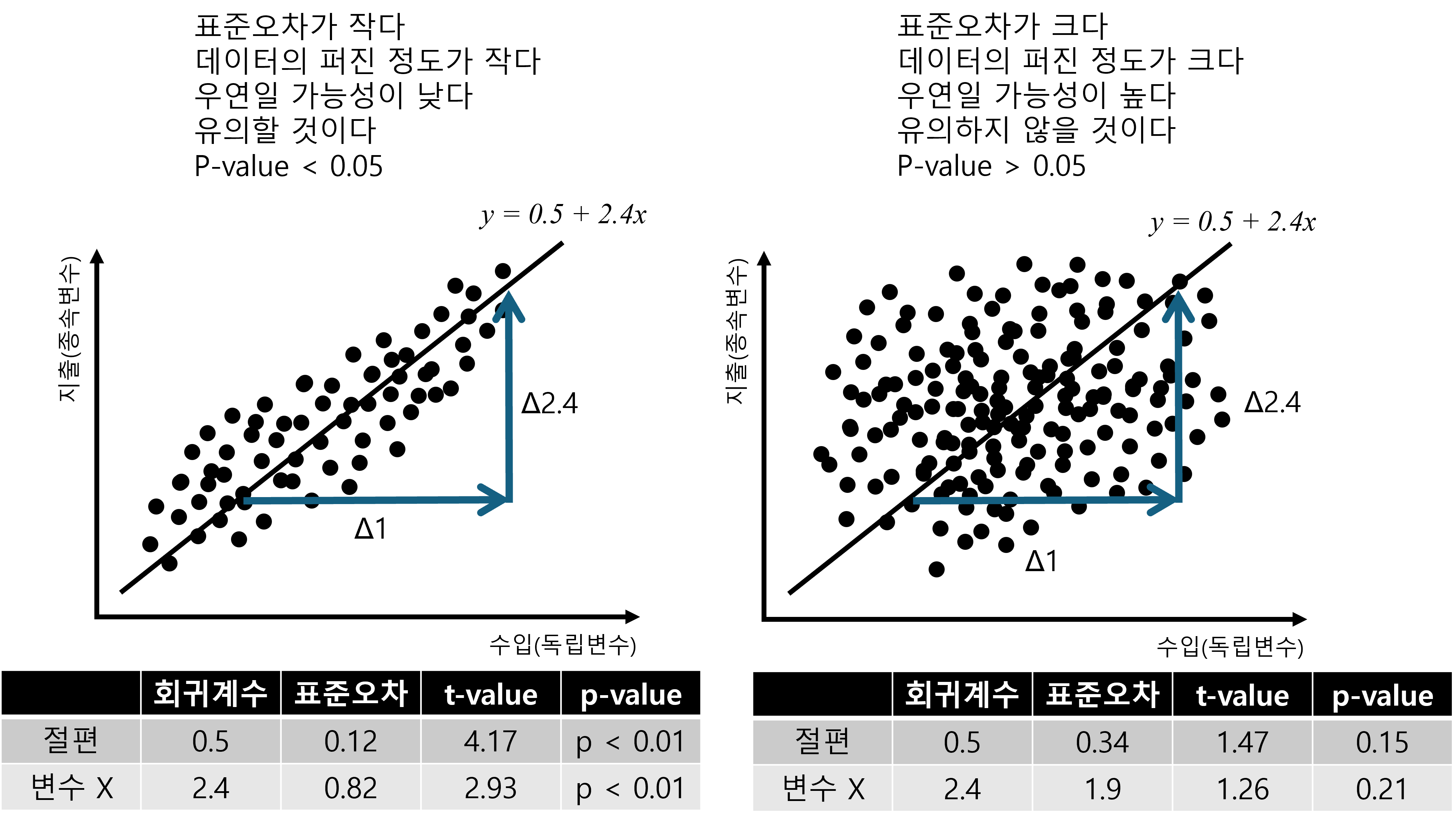
그러면, 먼저 좌측의 경우를 좀 더 자세하게 살펴보도록 하겠습니다.

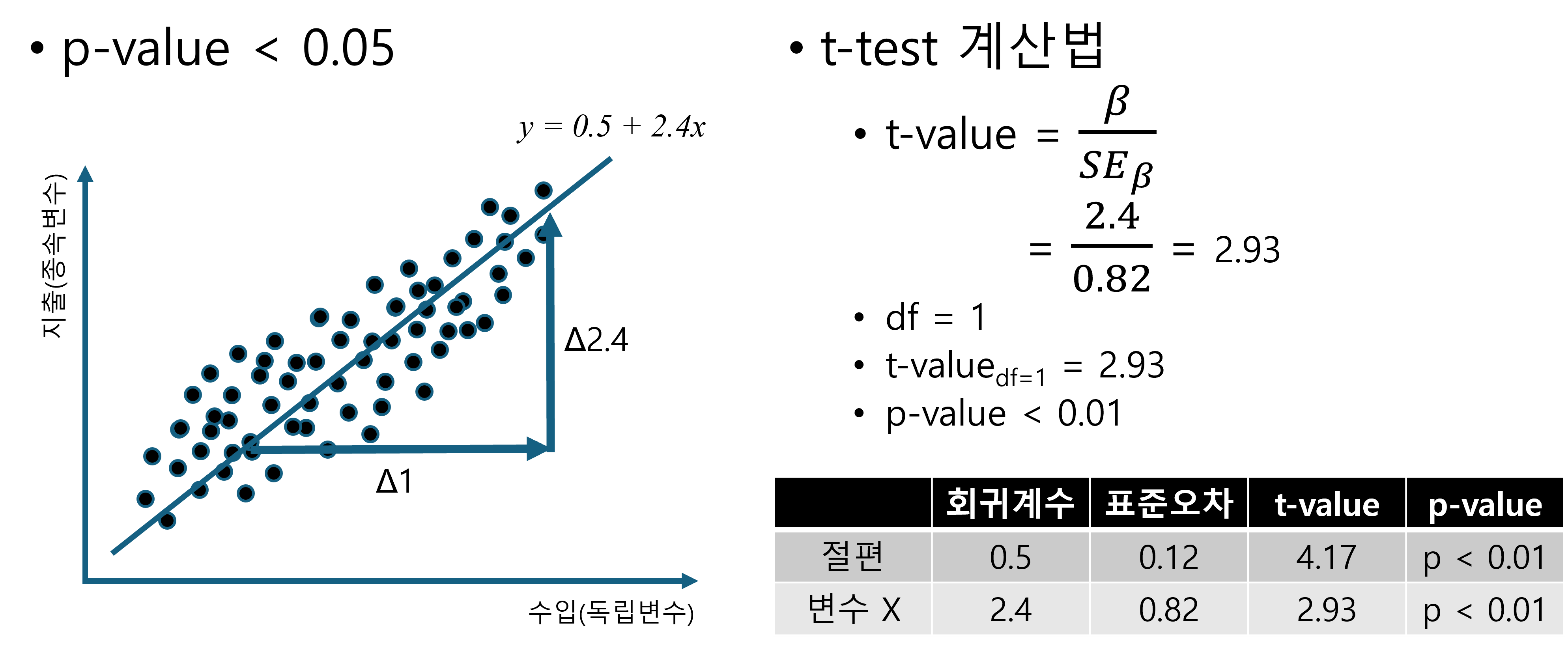
그림과 함께 t-test값을 계산하는 방법을 순서대로 보겠습니다. 사실상 순서랄 것도 없습니다. 우측 아래의 회귀분석 결과표에 나오는 회귀계수를 표준오차로 나눈 것이 바로 t-value 입니다. 그리고 이 t-value를 t-distribution을 이용해 p-value를 구하는 것입니다. 이때의 자유도(df=degree of freedom)은 1입니다. 왜냐하면, 변수 1개만 사용되어 그렇습니다. 자세한 내용을 알고 싶다면 통계학 전공을 하시길 바라며, mathematical statistics와 같은 책을 보시면 좀 더 도움이 되실 것입니다. 다시 위의 Figure 2.12 를 보면 결국 t-value값은 회귀계수 $\beta$를 표준오차 (SE=Standard Error)로 나눈 것입니다. 우리가 앞에서 공부한 t-value를 구하는 방법과 기본적으로 동일합니다. 여전히 왜 이렇게 하느냐고 물으실 수 있는데, 다시 한 번 강조하자면, 위의 회귀계수 $\beta$는 최소제곱법을 통해 계산된 수리적 해답입니다. 우리가 중고등학교에서 배운 복잡한 방정식을 푸는 것과 같은 것입니다. 여기까지는 수학의 영역이라고 할 수 있습니다. 이제 통계의 영역에 들어오고자 한다면 우리는 이 회귀계수 $\beta$ 즉 2.4라는 값이 우연히 나온 것인지 아닌지 궁금해 해야만 합니다. 이 회귀계수가 만약 우연히 나온 것이라면 수학적으로는 2.4이지만 통계적으로는 아무 의미없는 0이라고 보아야 하기 때문입니다. 만약 통계적으로 회귀계수 $\beta = 0$가 맞다면, 위의 경우 독립변수 $x$가 1 증가한다고 해도 통계적으로는 종속변수 $Y$가 0 증가하는 것이라고 보아야 합니다. 종속변수가 0 증가한다는 것은 결국 아무런 증감이 없다는 의미가 됩니다.

여기서 우리는 다시 앞에서 공부한 통계적 가설로 돌아가 볼 수 있습니다. 즉, 회귀계수 $\beta$에 대한 통계적 가설은 다음과 같습니다.

\[H_{0}: \beta = 0\] \[H_{a}: \beta \ne 0\]

만약 귀무가설($H_{0}$)이 채택된다면, 위의 회귀계수 $/beta$는 유의하지 않습니다. 반대로 대립가설($H_{a}$)이 채택된다면 회귀계수 $\beta$는 통계적으로 유의합니다. 우리가 보고 있는 표준오차가 작은 경우(Figure 2.12)는 p-value가 0.05보다 작아 대립가설이 채택된 경우입니다. 이 경우 연구가설이 채택되었다고 할 수 있습니다. 다시 한 번 말하자면, 연구가설이란 통계적 가설의 대립가설을 말로 풀어 쓴 것입니다.

그럼 이제 두 번째 표준오차가 큰 경우를 보도록 하겠습니다.

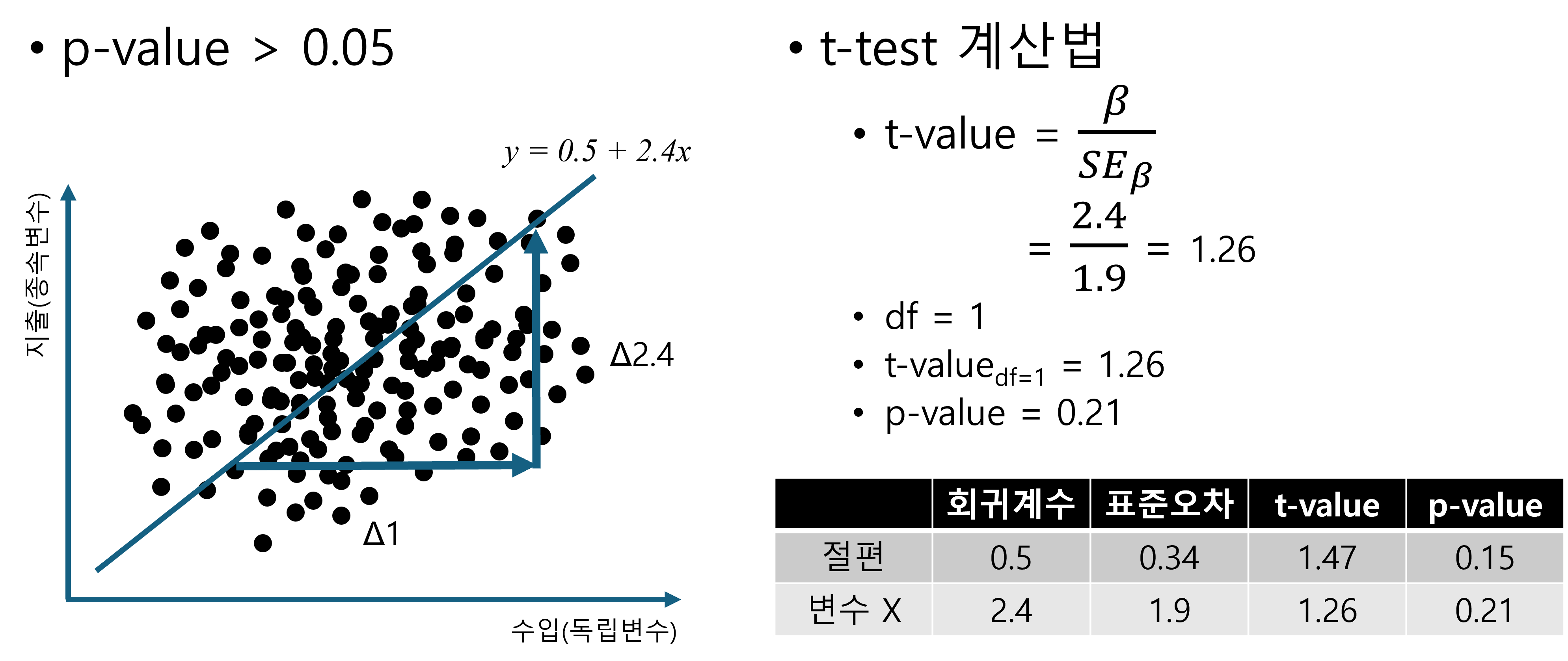
위의 Figure 2.13 를 보면 t-value값 1.26은 회귀계수 $\beta$ (2.4)를 표준오차(SE=Standard Error) 1.9로 나눈 것이므로 우리는 이 회귀계수 $\beta$ 즉 2.4라는 값이 우연히 나온 것인지 아닌지 궁금합니다. 이 회귀계수가 만약 우연히 나온 것이라면 수학적으로는 2.4이지만 통계적으로는 아무 의미없는 0이라고 보아야 합니다. 여기서는 이미 p-value가 0.21로 0.05 (5%)보다 크기 때문에 우리는 이 경우 회귀계수 2.4가 유의하지 않다고 결론 내립니다. 회귀계수가 유의하지 않다는 것은 수학적으로 회귀계수는 2.4이지만 통계적으로는 0이라고 보는 것입니다. 즉, 독립변수는 종속변수에 아무런 유의미한 영향이 없는 것입니다. 이는 아래에서 다시 한 번 살펴보겠습니다.

아마도 여전히 많은 분들이 회귀계수를 t-test로 검정하는 것에 대한 의문 내지는 이상함을 느끼실 수 있습니다. 그렇다면 이제 앞에서 공부한 t-test를 회귀분석으로 바꿔서 분석하여 이 두 분석방법을 비교함으로써 이 둘이 근본적으로 동일한 것이라는 사실을 한 번 살펴보겠습니다.

2.4.2 회귀분석과 t-test의 비교

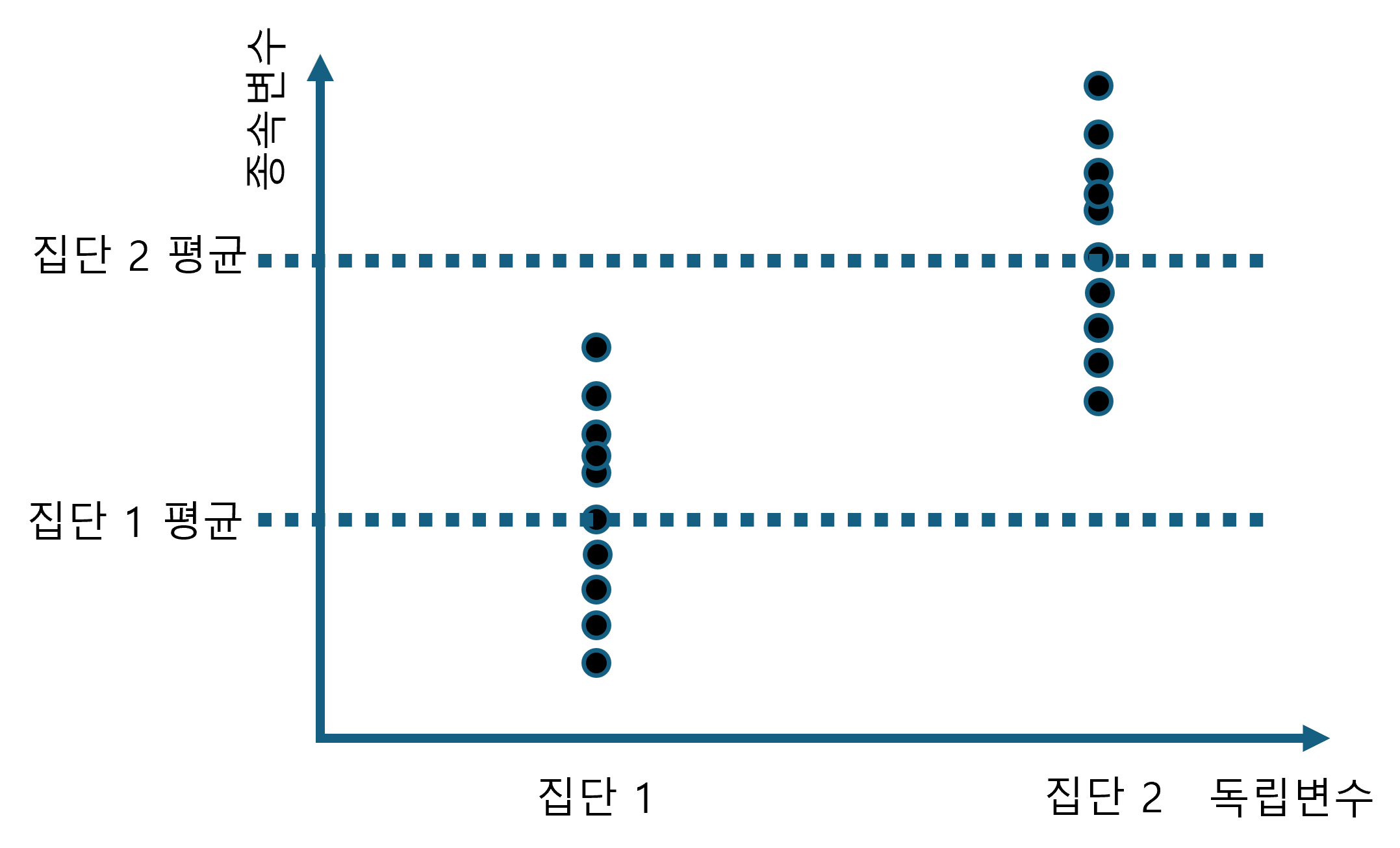
Figure 2.14 을 보면 두 집단의 평균값을 비교하고 할 때, 우리는 일반적으로 t-test를 사용합니다. 이 때의 t-value를 구하는 방법을 단순화 하면 아래와 같습니다.

\[t-value = \frac{평균_{집단1}-평균_{집단2}}{표준오차}\]

두 집단의 평균값의 차를 분자에 놓고 이 값이 우리의 주된 관심사가 됩니다. 문제는 이 차이값이 얼마나 커야 통계적으로 큰 것인지 혹은 얼마나 작아야 통계적으로 작은 것인지 알 수 없다는 것입니다. 그래서 비교대상으로 표준오차를 가져와서 분모에 놓고 나눠줍니다. 이렇게 해서 비율의 값이 나오면 이 값이 바로 t-value이고 이 값을 t-distribution을 이용해 p-value를 구하는 방식입니다.

그렇다면 이제 이 예제를 회귀분석으로 바꿔보겠습니다.

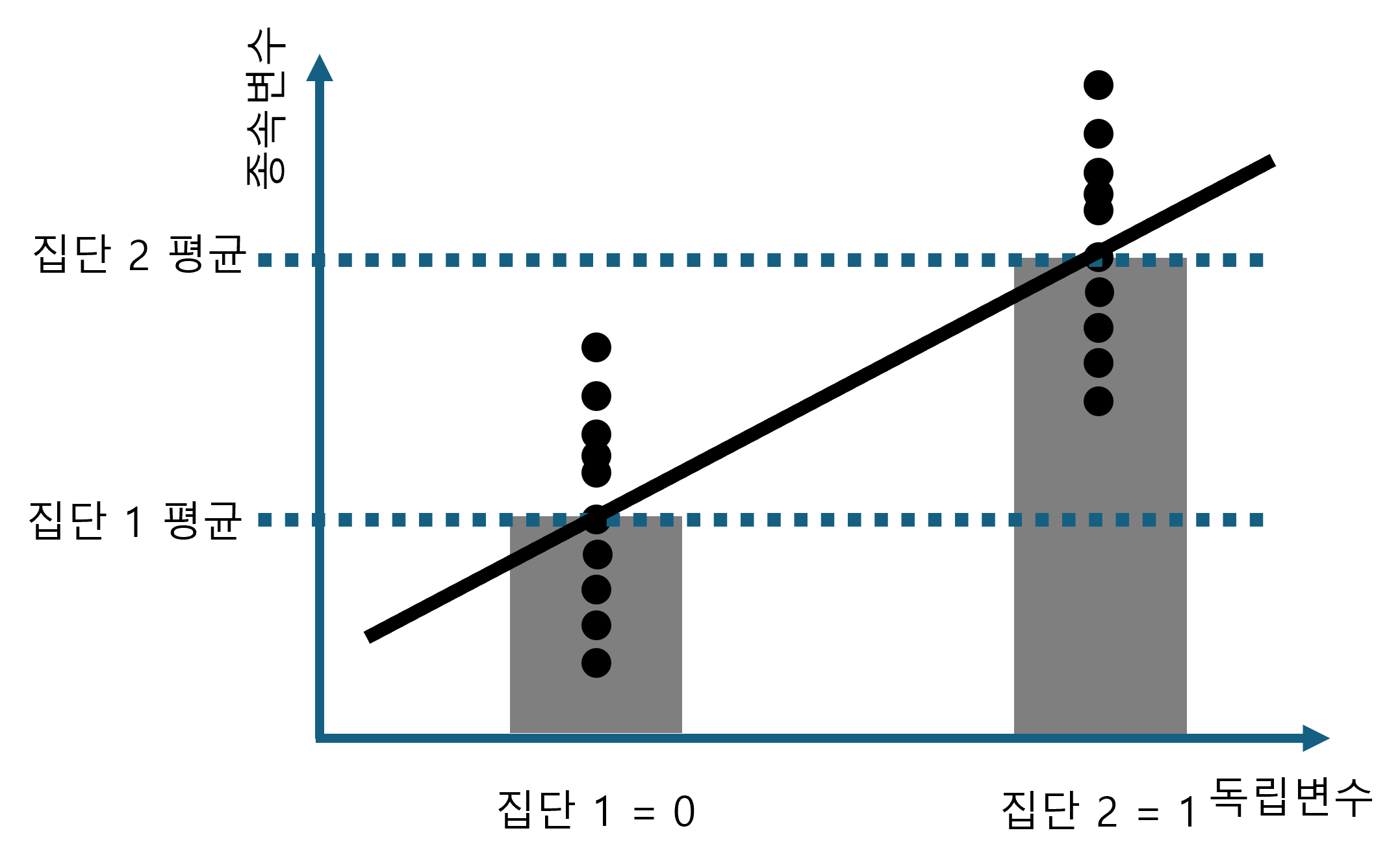
동일한 데이터를 회귀분석에 맞게 그림을 수정한 것이 Figure 2.15 입니다. 독립변수를 단순히 두 개의 집단이 아니라 하나를 0으로 코딩하고 다른 한 집단을 1로 코딩하는 더미변수 방식을 사용하였습니다. 더미변수에 대해서는 이후에 좀 더 자세하게 알아보겠습니다. 이렇게 했을 때, 회귀분석을 하면 이 회귀식은 두 집단의 평균값을 지나가는 직선이 됩니다. 앞에서도 이야기 했지만 회귀분석이란 평균값으로의 회귀를 의미합니다. 그러므로 두 집단의 평균값을 지나가는 직선의 방정식이 바로 회귀식이 됩니다.

이 회귀식을 $y = a + bx$라고 하면 기울기 $b$에 대한 t-value는 다음과 같이 유도할 수 있습니다. 먼저 앞에서 이야기한 것 처럼 기울기 $b$는 y값의 변화량을 x값의 변화량으로 나눈 것인데 이를 Figure 2.15 에 적용하면,

\[\beta = \frac{평균_{집단1} - 평균_{집단2}}{1 - 0}\]

여기서 두 집단의 평균값의 순서를 바꿔서 해도 큰 차이는 없습니다. 단지 양수이냐 음수이냐일 뿐인데 이또한 결국은 같은 값을 나타내게 되므로 위의 기울기를 기울기 $\beta$에 대한 t-value로 바꿔보면,

\[t-value = \frac{\beta}{표준오차} = \frac{\frac{평균_{집단1} - 평균_{집단2}}{1 - 0}}{표준오차} = \frac{평균_{집단1} - 평균_{집단2}}{표준오차}\]

이렇게 정리가 됩니다. 결론적으로 두 t-value는 동일한 값을 가지게 됩니다. 다시 말해, t-test로 두 집단의 평균값이 같은지 다른지 알아보는 방법과 이 데이터를 회귀분석하여 두 집단의 평균값을 지나는 회귀직선 $\beta$가 유의한지 아닌지 알아보는 방법은 동일한 방법이라는 의미가 됩니다.

2.4.3 회귀분석에서 주의할 점

이제 회귀분석에서 주의할 필요가 있는 내용을 몇 가지만 살펴보겠습니다. 먼저 우리가 앞에서 기울기가 0인 경우에 대해 잠시 이야기를 했습니다. 회귀계수 $\beta$의 기울기가 0인 경우를 그림으로 그려보면 어떤 경우가 될까요?

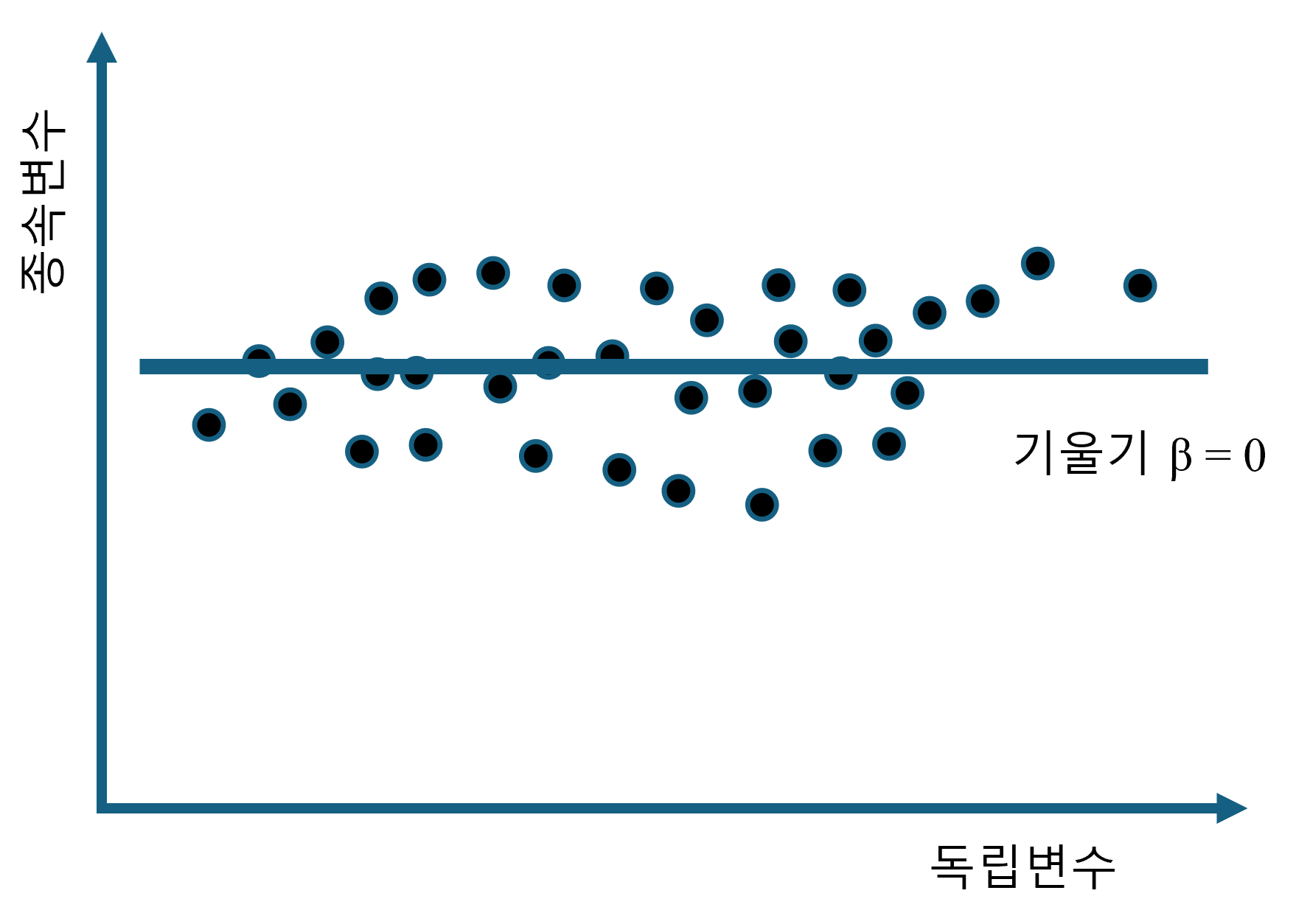
이렇게 되면, 독립변수가 아무리 증가하거나 감소해도 종속변수에는 아무런 영향이 없습니다. 그러므로 독립변수는 종속변수에 어떠한 의미있는 영향력이 없기 때문에 우리는 유의하지 않다라고 결론 내립니다. 이런 경우는 표준오차가 아무리 작아도 아무런 의미가 없습니다. 왜냐하면 t-value는 회귀계수 $\beta$를 표준오차로 나누는 것인데 시작부터 회귀계수가 0이라면 아무리 작은 표준오차로 나누어도 어차피 0이기 때문입니다.

그렇다면, 다음의 두 경우는 어떨까요?

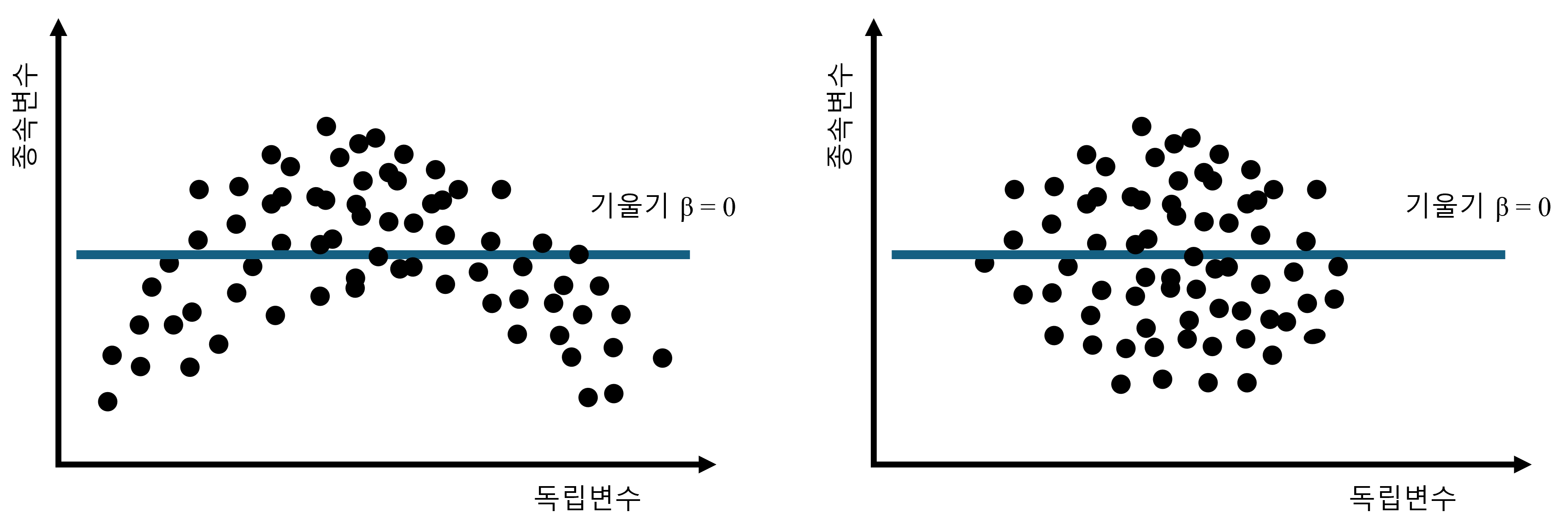
앞에서 그런 이야기를 한 적이 있습니다. 기본적으로 우리가 현재 공부하는 기초통계학은 대부분의 경우 Linear relationship을 전제하고 있다고요. Linear란 단어는 Line이라는 명사의 형용사형입니다. 즉, 선형의 라는 뜻이지요. 따라서 우리가 하고 있는 회귀분석 또한 선형관계를 전제로 합니다. 여기서 선형관계란 독립변수와 종속변수 사이의 관계를 의미합니다. 또한 여기서 말하는 선형이란 직선을 말합니다. 즉 독립변수와 종속변수의 관계가 서로 직선적인 관계이어야 한다는 것입니다.

문제는 위의 Figure 2.17 처럼 독립변수 $x$가 증가할 때, 종속변수 $y$가 증가하다 감소하면 이는 직선이 아닌 곡선의 관계가 되므로 비선형관계 즉 non-linear relationship이 됩니다. 이렇게 되면, 우리가 공부한 회귀분석은 아무런 소용이 없습니다. 위에서 보듯 회귀분석을 해보면 결과가 기울기 $\beta$는 0이라고 나타납니다. 문제는 이 기울기 값 자체가 전혀 신뢰할 수 없다는 데에 있습니다. 또한 두번째 그림처럼 독립변수와 종속변수의 관계를 산포도로 그렸을 때, 공 모양으로 둥글게 나오면, 이 또한 둘 사이에 아무런 관계가 없다는 의미가 됩니다. 왜냐하면 독립변수가 증가하건 감소하건 종속변수의 방향을 예측할 수 없기 때문입니다.

정리를 해 보면,

만약 데이터가
- 곡선 형태로 되어 있다면 기울기는 0 이다
- 원(구) 형태로 되어 있다면 기울기는 0 이다
- 직선의 형태로 되어 있지 않다면 분석할 수 없다
회귀분석 전에 산포도(scatter plot)을 찍어 보아야 한다
- 직선형태의 데이터 분포가 나타나지 않는 경우 다른 방법을 찾아야 하는데,
- 왜냐하면 결국 회귀분석이란 $y = a + bx$ 의 직선의 방정식을 구하는 것이므로,
회귀계수의 기울기는 결국 t-test의 평균값 차이와 동일한 개념이 되어
- t-test를 이용해 유의성을 검정한다

마지막으로 회귀분석과 t-test의 통계적 가설을 비교해 보면,

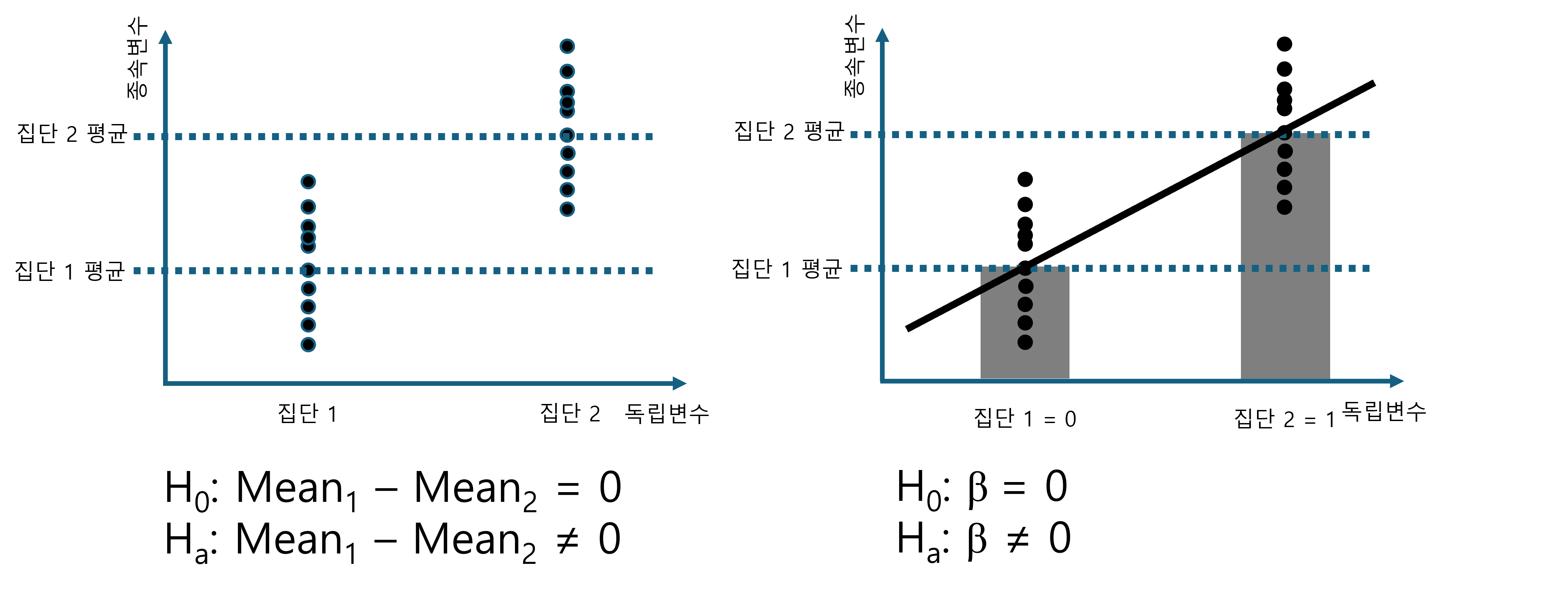
위와 같이 됩니다.

이제 여러분들은 회귀분석의 모든 기본적인 내용을 마스터했습니다. 이제 회귀분석과 관련된 부가적인 내용들에 대해 하나씩 알아보겠습니다. 사실 회귀분석은 많이 사용되는 만큼 부가내용이 많습니다. 그러니 하나씩 차근차근 따라 오시길 바랍니다.

수고 많으셨습니다.

Youtube 바로 가기

2.5 R²를 어떻게 해석해야 할까?

2.5.1 통계의 의미와 R²

이 강의를 시작할 때, 제가 통계란 무엇이라고 했는지 기억나시나요?

저는 통계란 분산의 마법이라고 표현합니다. 물론 아직도 이 표현을 무슨 미사어구 정도로 생각하시는 분들도 있겠지만, 통계를 공부하면 할 수록 이 말이 사실이라는 점을 알게되실 겁니다. 앞의 t-test부터 ANOVA 그리고 회귀분석에 이르기까지 결국 모든 것이 분산과 관련이 있는 것들이었습니다.

이제 R²로 돌아가 봅시다. 회귀분석을 약간이라도 아는 분들은 아마도 이 R²에 대해서 들어보셨을 겁니다. 어느 정도 통계지식이 있는 분들이라면 더더욱 잘 아시리라 생각됩니다. 그렇다면 이 R²는 대체 무엇일까요? 일단 답을 알아보기 전에 회귀분석이 무엇인지 다시 한 번 생각해 보아야 합니다.

회귀분석이란 종속변수와 독립변수 사이의 인과관계를 논리적/이론적으로 전제하고 톡립변수를 이용해 종속변수를 설명하려는 시도입니다. 이때 회귀계수를 해석할 때는 $x$가 1 증가할 때, $y$가 $\beta$만큼 증가한다고 해석합니다. 여기서 회귀분석이란 결론적으로는 종속변수 $y$의 분산을 독립변수 $x$로 설명하려는 노력이다 라고 표현할 수 있겠습니다. 그렇다면 도대체 독립변수로 종속변수의 무엇을 설명하려는 것일까요? 그것은 바로 종속변수의 분산을 설명하는 것이 회귀분석의 목적이라는 것입니다.

그러므로, 회귀분석을 포함한 통계적 분석이란 이론적 논리적 근거를 기반으로 종속변수를 설명할 수 있는 모델을 만드는데, 이 모델이란 바로 독립변수를 설정하는 것을 의미합니다. 여기서 설정된 모델 즉 독립변수를 이용해서 종속변수의 분산을 설명하는 것이 바로 통계적 분석이고, 만약 우리가 만들 모델이 큰 문제가 없다면, 즉 종속변수의 분산을 충분히 잘 설명했다면, 우리의 모델로 설명하고 남은 종속변수의 분산은 단지 random한 분산일 뿐입니다. 즉, 큰 의미가 없는 분산이라는 의미가 됩니다.

여기서 R²의 의미가 발견됩니다. R²란 종속변수 전체의 분산중에서 모델에 의해 설명된 분산의 비율을 의미합니다. 아래의 그림을 보면 좀 더 이해가 쉬울 수 있습니다.

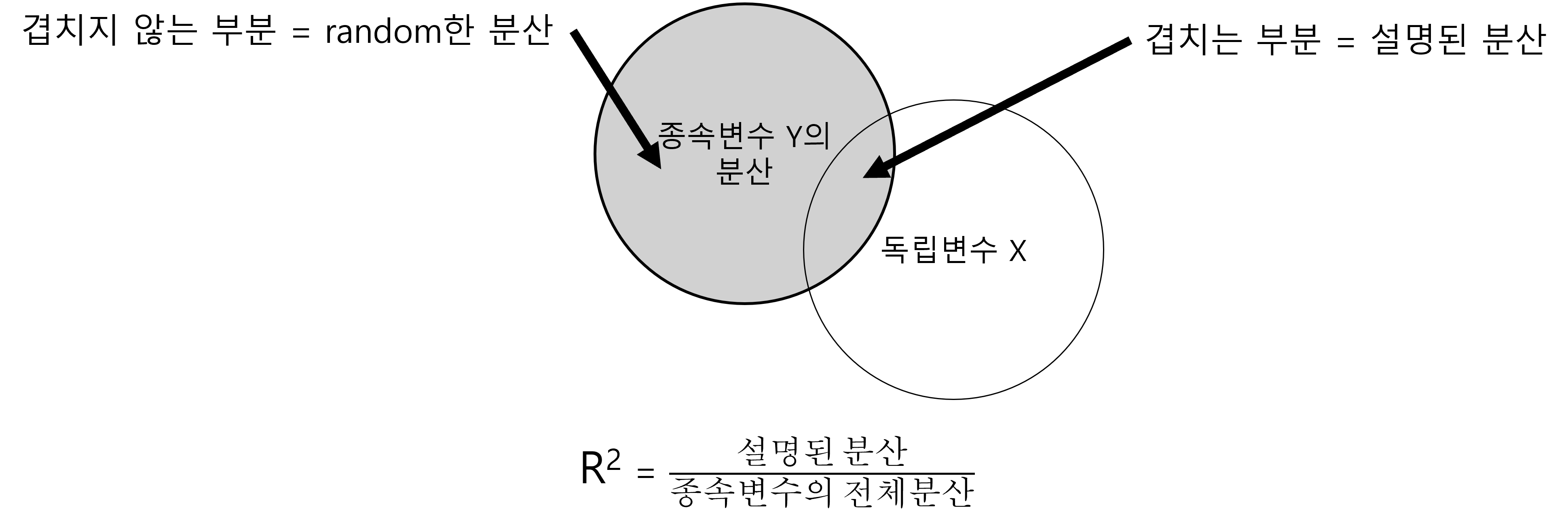
그렇다면 앞에서 본 두 개의 표준오차가 다른 경우를 다시 보고 이야히 해 봅시다.

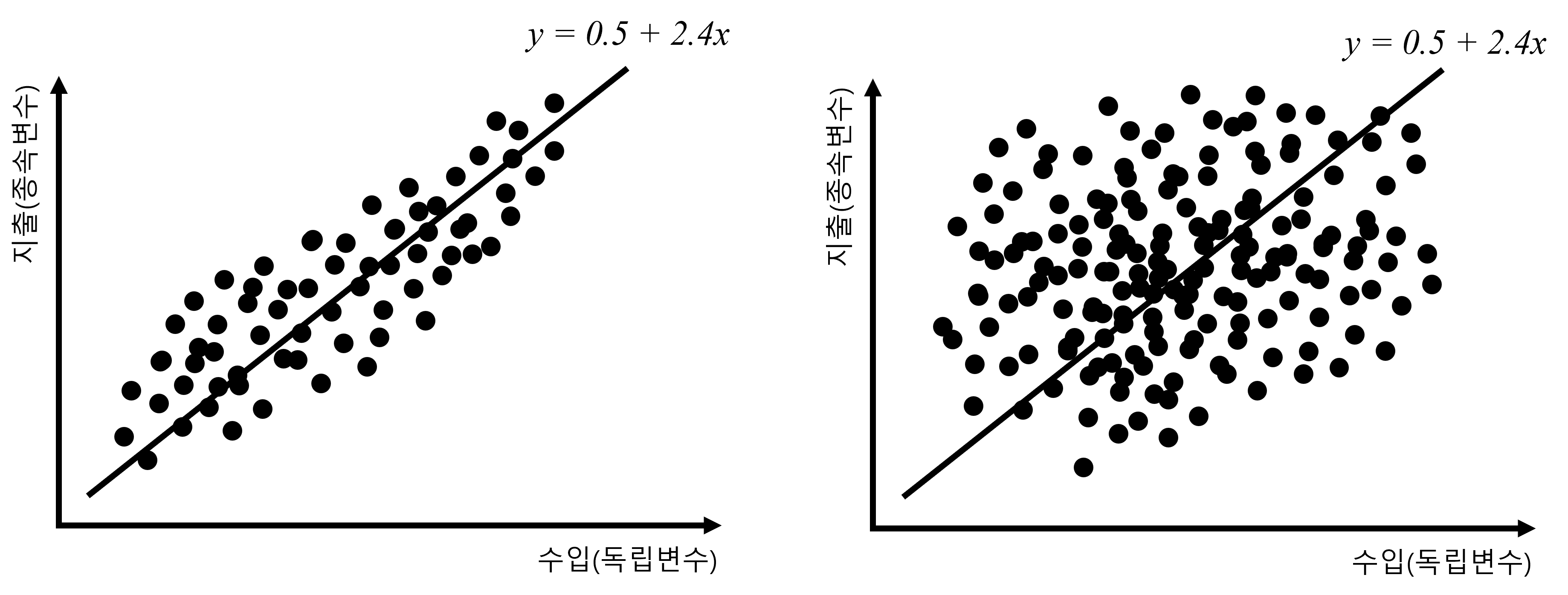
Figure 2.20 의 좌측의 경우는 분산 설명력이 높은 경우이고, 우측의 경우는 분산 설명력이 낮은 경우입니다. 즉, 회귀직선을 중심으로 데이터가 모여 있다면 분산 설명력 즉 R²가 높은 경우이고, 회귀직선을 중심으로 데이터가 넓게 퍼져 있다면 분산 설명력 즉 R²가 낮은 경우입니다.

2.5.2 높은 분산설명력과 낮은 분산설명력

그럼 이제 하나씩 살펴 보겠습니다.

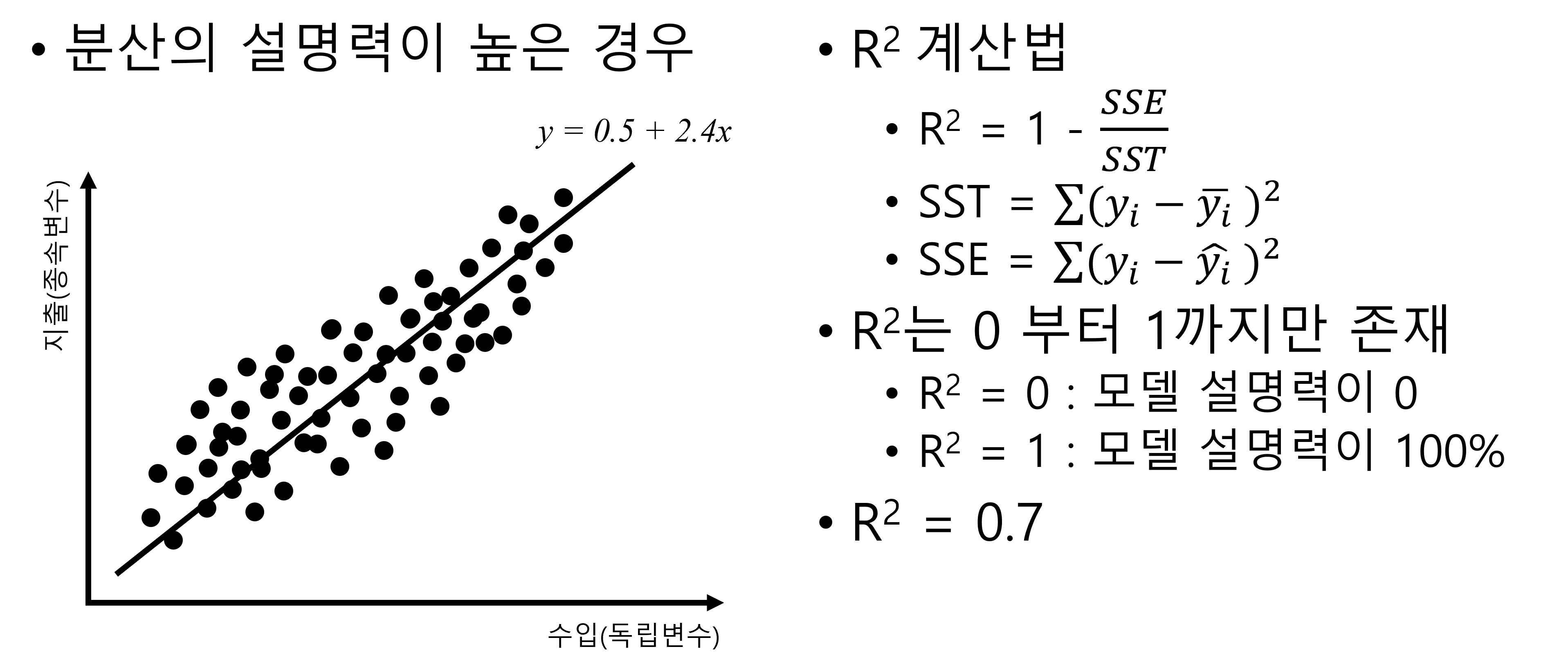
Figure 2.21 은 분산 설명력이 높은 경우입니다. R²의 계산법을 보면,

\[R^{2} = 1 - \frac{SSE}{SST}\]

여기서 SSE는 Sum of Squared Error의 약자이고 SST는 Sum of Squared Total의 약자입니다. SST는 종속변수의 전체분산을 의미하고 SSE는 설명되지 않은 random error의 분산을 의미합니다. 이 비율을 1에서 빼기 때문에 R²는 설명된 분산의 비율을 의미 합니다. 좀 더 자세하게 들여다 보면,

\[SST = \sum(y_i -\bar{y_i})^2\]

여기서 SST는 일반적으로 분산을 계산하는 것을 생각하면 동일합니다. 일반적인 분산의 계산법의 분자부분이 SST입니다. 위의 식을 보면 각 데이터의 관찰값에서 평균값을 뺀 것으로 제곱하여 합하는 것입니다. 이는 분산 계산시 분자부분입니다. 이것이 바로 total variance라고 보시면 되고 SST입니다.

\[SSE = \sum(y_i -\hat{y_i})^2\]

반면에 설명되지 않은 분산은 error라고 할 수 있는 $y_i -\hat{y_i}$입니다. 여기서 $\hat{y_i}$은 회귀분석에 의해 구해진 회귀직선입니다. 따라서 SSE는 데이터의 관찰값과 회귀직선 간의 차이의 제곱합입니다.

다시 Figure 2.21 로 돌아가 보면 결국 이 경우의 R²는 0.7로 꽤 높은 편입니다. R²는 0부터 1까지의 값만 가지게 됩니다. R²가 0이라는 의미는 독립변수가 전혀 종속변수의 분산을 설명하지 못했다는 의미이고, R²가 1이라는 의미는 독립변수가 종속변수를 완벽하게 설명했다는 의미입니다. 이런 경우 데이터의 모든 점들이 회귀식 위에 올라가 있습니다.

그렇다면, 분산의 설명력이 낮은 경우는 어떨까요?

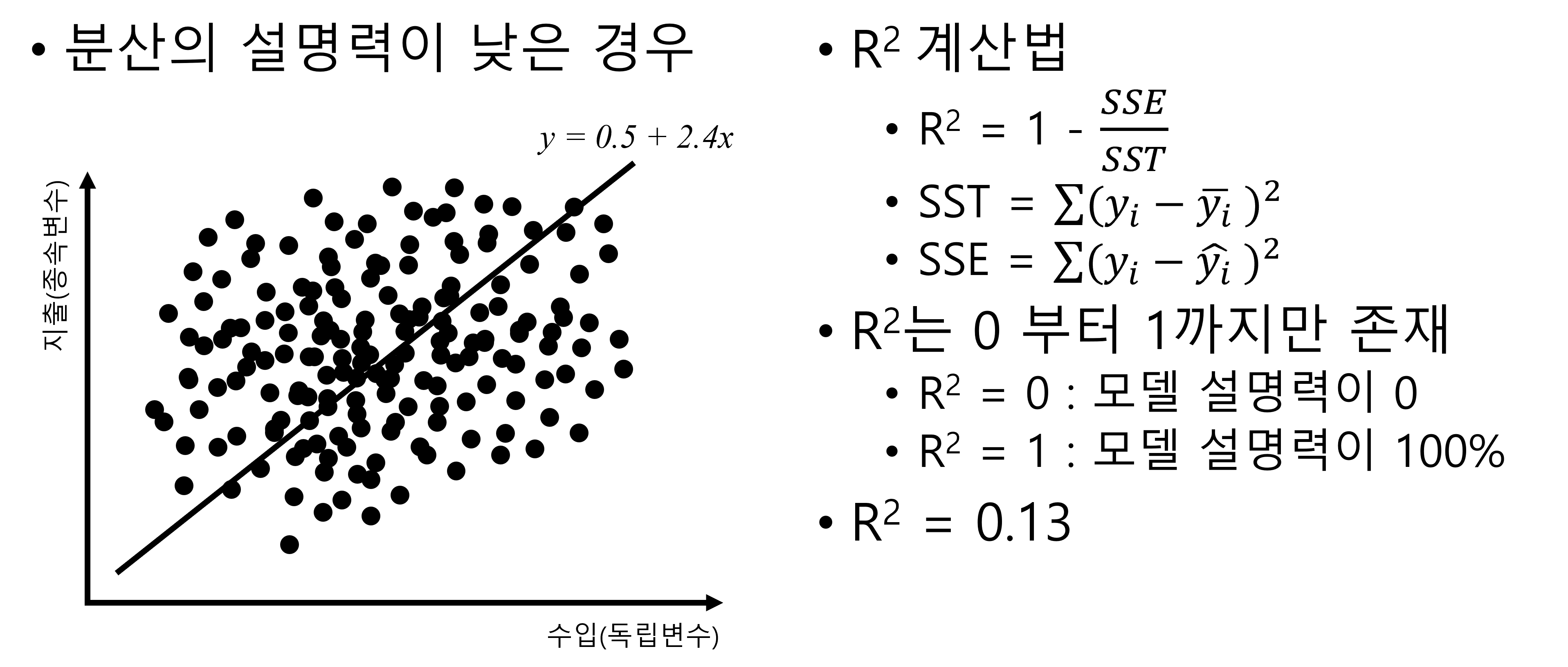
Figure 2.22 에서 보듯, R²는 0.13에 불과합니다.

다시 한 번, 정리해 보자면, R²는 모델의 분산 설명력이고, 이는 우리가 만들 모델(독립변수)이 우리의 종속변수의 분산을 얼마나 잘 설명했는지를 의미합니다.

2.5.3 애증의 R²

그렇다면, R²가 높은 것이 무조건 좋을까요?

불과 10여년 전까지만 해도, 이 문제로 교수님들 사이에서도 말이 좀 있었습니다. 과거에는 이 R²를 너무 과하게 중요시 하는 문화가 일부 있었기 때문입니다. 물론 그렇다고 R²가 무시되어도 된다는 말은 아닙니다. R²가 나름의 의미를 분명하게 가지고 있긴 하나, R² 하나 때문에 연구나 분석 전체가 무너지는 일은 그다지 좋지 않다는 의미입니다. 연구나 분석이 문제가 있다면, R² 하나 때문이 아니라 이미 연구의 시작부터 논리적 혹은 이론적으로 문제가 많았을 것이고 그러한 결과가 단순히 R²에 반영될 수는 있어도, 만약 다른 문제가 없는데 단순히 R²가 낮다는 이유만으로 연구나 분석 자체를 부정하는 것은 위험하다는 의미입니다.

뿐만 아니라 단순히 R²가 높으냐 낮으냐 보다 R²를 보기 전에 회귀분석 자체가 건강한지 아닌지 확인하는 작업이 더 중요할 수 있습니다. 예를 들어 R²를 확인하기 전에 잔차도(residual plot)을 확인하여 잔차(residual)가 랜덤하게 분포하느지 확인해야 합니다. 여기서 잔차란 위의 $y_i -\hat{y_i}$을 의미합니다.

또한, 단순한 , R²가 위험한 또 다른 이유는 다음과 같습니다. 만약 R²값을 올리는 것만이 회귀분석의 유일한 목적이라면, 우리는 가능한 사용할 수 있는 모든 독립변수를 전부 다 넣어서 모델을 만들면 됩니다. 이러한 경우를 우리는 Dumping이라고 합니다. 독립변수를 가능한 한 많이 Dump 하면 아주 약간의 R²를 증가시킬 수 있기 때문입니다. 물론 이런 경우 R²가 많이 올라가지는 못하고 0.000001 이런식으로 증가되기는 합니다. 문제는 앞서 잠깐 이야기 했듯이 독립변수의 추가는 자유도(df=degree of freedom)의 손실을 의미합니다. 독립변수 1개는 자유도 1의 손실입니다. 따라서 무조건 적인 독립변수의 무한 투입은 상당한 손실일 뿐입니다. 더불어 이렇게 투입된 변수는 그 변수 하나 하나가 유의하지 않습니다.

마지막으로 최근 빅데이터로 인해 많이 알려진 과적합(overfitting)문제입니다. 사실 이 과적합 문제는 데이터가 많고 적음의 문제는 아닙니다. 조금만 어려운 중급정도의 회귀분석을 해보면 over-identification이라는 용어가 등장하는데 이는 우리가 빅데이터 분석에서 말하는 과적합(overfitting)과 유사한 개념입니다. 쉽게 말해, 높은 R²를 위해 독립변수를 과하게 투입하거나 혹은 현재 분석하는 데이터에서만 유의할 만한 독립변수 중심으로 모델을 구성할 경우 과적합의 문제가 발생합니다. 여기서 과적합이란 현재 분석한 해당 데이터에 대해서는 높은 R²를 보이지만, 다시 데이터를 수집하여 동일한 모델을 적용할 경우 R²가 매우 낮게 나오게 되는 경우를 의미합니다. 통계적 분석에 경험이 없으신 분들의 경우 이것이 왜 문제냐고 생각하실 수 있습니다.

문제는 우리가 데이터 분석을 하고 통계적 방법을 적용하는 목적이 현재 가지고 있는 데이터를 잘 설명하는 것이 궁극적인 목표가 아니라는 점입니다. 특히 사회과학은 이론과 논리 그리고 기존 연구를 바탕으로 가설을 세워 이 가설을 검정할 만한 데이터를 수집하여 이를 통계적 방법으로 검정하는 과정르 거쳐 가설의 채택여부를 결정하고, 최종적으로 채택된 가설은 본 연구 혹은 현재의 데이터 뿐만 아니라 다른 데이터와 다른 경우에도 채택될 수 있는 일반화(generalization)를 궁극적인 목표로 하기 때문입니다.

현대의 많은 사회과학 연구나 분석이 이러한 일반화(generalization) 보다는 현재의 데이터를 이용해 현재의 연구를 보다 돋보이게 하려는 시도가 많다보니, 학계에 출판된 (published) 연구들 조차 재확인(replication)이 되지 않는 경우가 많습니다. 이는 연구자의 실수이든 의도된 결과이든 상당한 문제가 될 수 있으므로 매우 주의해야 할 부분입니다.

2.5.4 회귀분석과 잔차도

그렇다면 여기서 잔차도의 예를 두 개 보겠습니다.

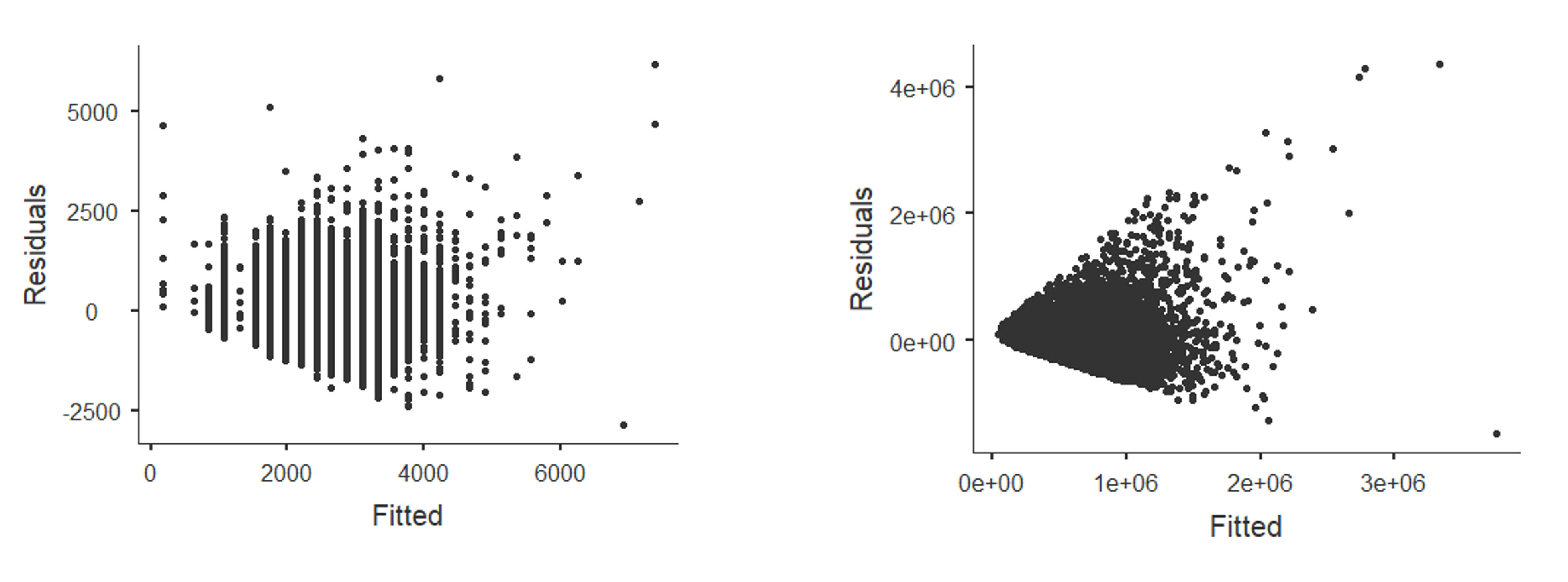
Figure 2.23 의 좌측은 무난한 수준의 잔차도입니다. 완벽한 random이라고 말하긴 좀 애매하지만 큰 무리는 없어보입니다. 문제는 우측과 같은 경우입니다. 우측은 제가 가지고 분석했던 실제 데이터입니다. 잔차도는 random하게 점들이 찍혀야 하는데 우측의 잔차도는 명확한 패턴이 보입니다. x축의 크기가 커질수록 y축을 중심으로 데이터가 확장하는 패턴을 가지고 점들이 퍼져 있는 것을 확인할 수 있습니다. 보통 매출이나 이익액 등의 변수를 사용하면 흔하게 발생하는 문제입니다.

다음은 앞서 R²의 문제점에 대한 대안입니다. 앞서 독립변수를 무한대로 dumping하면 아주 근소하지만 R²는 증가한다고 이야기 했습니다. 문제는 이렇게 독립변수를 증가시킬 때마다 자유도를 1씩 잃는 다는 것이 문제입니다. 따라서 이에 대한 보정이 필요합니다. 여기서 보정이란, 추가된 독립변수가 자유도 1을 잃고도 충분히 분산을 설명했는지 여부를 의미합니다. 결론적으로 손실인 자유도를 감안한 R²값이 필요하다는 의미이지요. 이것이 바로 수정된 R² (adj. R²)입니다. 일반적으로는 논문을 작성할 때 이 두 값 (R²와 adj. R²)을 모두 리포트 합니다. 만약 두 값의 크기가 심하게 다르다면 이는 의미 없는 독립변수를 너무 많이 dump했다는 뜻이 되므로 투입된 독립변수에 대한 재고가 필요합니다.

마지막으로 과적합(overfitting)에 대해 살펴보자면, 일반적으로 우리는 표본을 수집해서 데이터를 분석합니다. 이 이야기는 대부분의 경우 데이터 자체가 그다지 많지 않다는 의미이기도 하고 이는 현재의 데이터에서 높은 R²를 보인 모델이 다른 데이터에서는 전혀 제대로 작동하지 않을 수 있다는 의미입니다. 사실 그래서 지금의 빅데이터 분석에서는 자연스럽게 데이터를 Testing set와 validation set으로 나누어 Testing set으로는 모델을 만들어 테스트하고, 여기서 완성된 모델을 다시 validation set으로 검증하는 과정을 거칩니다. 문제는 단순 설문조사 등으로 수집한 데이터의 경우 이렇게 두 개의 세트로 나눠서 분석을 진행할 만큼 데이터가 크지 않은 경우가 많다는 것입니다. 물론 이 문제를 해결하기 위한 별도의 방법들이 또한 요즘에는 만들어지고 있지만 기초 통계를 배우는 과정에서 말하기는 좀 어렵긴 합니다. 어쨋거나 너무 과도한 R² 집착으로 인한 과적합은 부정적인 결과를 가져온다는 것을 기억하는 것은 중요합니다.

오늘의 내용을 정리해 보자면,

R²는 애증의 대상이라는 것입니다
- R² 는 모델(독립변수)이 종속변수의 분산을 얼마나 잘 설명했는지를 의미하고,
- R² 가 높다는 것은 모델의 설명력이 높으므로 나름 좋은 의미입니다
- 그러나, 높은 R²가 모델의 정당성을 모두 해결해주지는 않습니다
R²의 단점은,
- R²를 높이는 것이 단일한 목적일 경우 무한히 많은 독립변수를 추가하면 되지만,
- 독립변수의 추가는 결국 비용이고 손해라는 점이 중요합니다 (자유도 1 손실)
- 그러므로 adj. R2(수정된 R2)를 같이 사용하는 것이 좋습니다
마지막으로, R² 보다 중요한 것은
- 모델에 사용된 독립변수의 논리적/이론적 근거가 보다 중요하다는 것입니다
- 일단 넣어보고 R²만 높아지면 된다는 생각은 매우 위험합니다

Youtube 바로 가기

2.6 회귀분석의 표준화계수

2.6.1 표준화계수를 알고 사용할까?

제가 한국에 와서 가장 놀란 것 중의 하나가 바로 표준화계수입니다. 논문심사를 들어가 보면 모든 논문에 표준화계수가 꼭 들어가고 만약 들어가 있지 않으면 무슨 큰 일이나 난 것처럼 심사위원들이 학생을 몰아세웁니다. 마치 기본도 되어 있지 않다는 듯 말이지요. 개인적으로는 미국에서 공부할 때 책으로만 알고 있던 것이 바로 표준화 계수인데, 한국에 오니 이게 이렇게 중요할 줄 몰랐습니다. 문제는 그래서 다른 심사위원들에게 표준화계수에 대해 물어보면 정확하게 아는 분도 거의 없거니와 이 표준화계수를 정확하게 해석하는 분은 보기 드물었습니다. 참 알 수 없는 노릇이지요.

일단 표준화계수에 대해서 알아봅시다.

Figure 2.24 은 회귀분석 결과표입니다. 좌측이 Jamovi의 결과이고, 우측이 SPSS의 결과입니다. 대부분의 통계 프로그램의 경우 좌측의 Jamovi처럼 표준화계수를 Default로 제시하지 않습니다. 별도의 명령을 주거나 클릭을 하면 표준화계수를 리포트 하는 것이 일반적입니다. 예외적으로 SPSS는 표준화계수를 Default로 리포트합니다. 아마도 한국에서 표준화계수를 중요시하는 이유가 바로 SPSS 때문이 아닐까 생각합니다. 대략 2000년대 초반까지는 SPSS를 대체할만한 개인 소프트웨어가 거의 없었기 때문에 이해는 되나 요즘은 워낙 좋은 소프트웨어가 많아서 굳이 SPSS를 고집할 필요는 없다고 생각됩니다.

그렇다면, 표준화계수는 무엇이고 어떻게 해석해야 할까요?

2.6.2 표준화계수의 예제

표준화계수의 예제를 하나 만들어 보겠습니다. 간단한 회귀분석을 해보도록 하겠습니다.

종속변수: 주택가격(price)
독립변수
- sqft_living: 거실 사이즈
- floors: 주택의 층수
- waterfront: 물가(강/바다)에 근접한 주택인지의 유무
  - 더미변수(1: 있음, 0: 없음)

제가 유투브 녹음을 할때, waterfront의 의미를 정확하게 몰랐는데 나중에 알았네요. 수영장이 아니라 물가에 인접한 주택을 의미하는 것이었습니다. 여기서 의도하는 것은 거실의 크기가 크거나 층수가 높은 주택, 혹은 물가에 인접한 주택이 가격이 높을 것이라는 가정하에 독립변수를 넣었습니다. 아래는 그 결과표입니다.

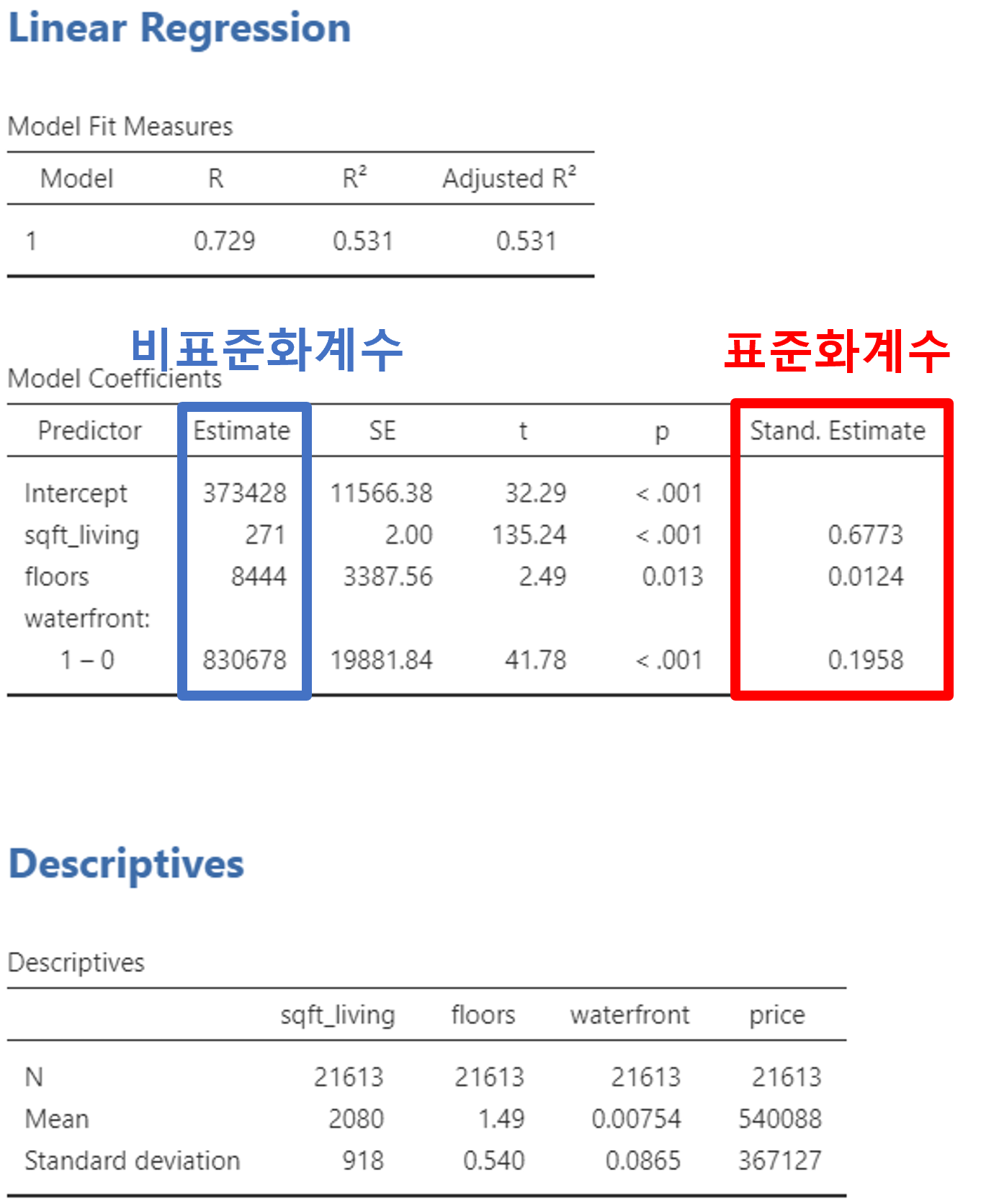
Jamovi에서 클릭 한 번만 하면 가장 우측에 표준화계수를 리포트해줍니다.

표준화계수의 장점은 종속변수에 대한 독립변수들의 단위(scale)을 통일시킨 계수로서 표준화계수의 단위(scale)는 없어져 모든 독립변수를 같은 단위(scale)상에서 비교 가능하다는 것입니다. 이게 무슨 뜻인가 싶으실 겁니다. 쉽게말해 표준화계수의 값을 해석할 때는 원래 변수의 단위(scale)이 사라지고, 모든 독립변수는 단위가 없는 것으로 변경된다는 의미입니다. 여전히 어렵죠? 일단 그렇게 이해하고 뒤에서 자세한 설명을 해보겠습니다.

표준화계수의 또다른 특징이라면, 표준화계수에 의한 회귀직선은 원점(0,0)을 지나가는 회귀직선이 되고, 이로 인해 절편(intercept)은 0이 됩니다. 더불어 단위(scale)가 없고 모든 독립변수의 단위가 동일하게 되었기 때문에 회귀계수의 크기 비교가 가능해집니다.

표준화라는 단어에서 혹시 눈치를 채신 분도 있을텐데, 처음부터 모든 변수를 표준화해서 회귀분석을 하면 표준화계수와 동일한 결과를 얻을 수 있습니다. 궁금하신 분들은 한 번 시도해보시길 바랍니다. 여기서 표준화란 z-transformation을 의미합니다. 앞에서 공부한 z-test의 z-value를 떠올리시면 됩니다.

2.6.3 표준화계수의 계산방법

표준화계수를 계산하는 방법은 다음과 같습니다.

\[표준화계수 = 비표준화계수 \div \frac{SD_y}{SD_x} = 비표준화계수 \times \frac{SD_x}{SD_y}\]

\[SD_x = 독립변수의 표준편차,\; SD_y = 종속변수의 표준편차\]

그렇다면 Figure 2.25 을 이용하여sqft_living의 표준화계수를 계산해 보면,

\[표준화계수 = 271 \times (918 \div 367127) = 0.677\]

소수점 자리가 약간 차이가 나긴 하지만 결과표에 나온 표준화계수와 동일합니다. 그렇다면 무슨 뜻일까요?

2.6.4 표준화계수의 해석

가장 많이 사용되는 해석방법은 이렇습니다. 결과표의 세 개의 독립변수의 표준화계수를 비교해 보면 sqft_living의 표준화계수가 0.6773으로 가장 큽니다. 이렇게 결과가 나오면 일반적으로 세 독립변수 중에서 sqft_living의 영향력이 가장 크다고 해석합니다. 사실 한국에서는 이렇게 해석하고 끝이 나긴 하는데, 이게 엄밀하게 따져보면 상당히 위험한 해석일 수 있습니다. 지금 이 예제에서는 나머지 두 변수의 표준화계수가 워낙 작아서 이렇게 해석할 여지가 있기는 하나 통계적 의미를 따져본다면 세 변수의 크기를 통계적으로 비교하여 p-value를 확인한 것이 아니므로 일종의 rule of thumb이 라고 할 수 있습니다. 이는 쉽게 말해 운 좋게 맞았다라고 하는 것이지요. 최근 통계학에는 이런 문제를 해결하기 위해 relative importance라는 주제가 다양한 방법으로 발전 중에 있습니다. 문제는 매우 어렵다는 것입니다. 뿐만 아니라 단지 누가 더 영향력이 크냐를 알기 위해 사용하기에는 그다지 현실적인 의미가 약하다고 할 수 있습니다. 왜냐하면, 이 예제의 경우 거실의 크기가 주택가격에 절대적이기 때문에 주택 가격을 높이기 위해 거실 크기만 크게하면 된다라는 해석은 오히려 문제를 일으킬 수 있습니다. 우선 건축비용의 문제가 있을 수 있기도 하지만 법적인 규제는 전혀 고려되지 않은 것이기도 하고 실제로 다른 변수들을 조정하는 비용대비 거실을 크게하는 비용이 더 효율적이거나 효과적인지는 알 수 없기 때문입니다.

다음으로 표준화계수의 해석에 대해 이야기 해 보겠습니다.

비표준화계수의 경우 sqft_living이라는 변수를 예로 들면, 거실 사이즈가 1 feet² 커지면 주택가격이 271 US dollar 오른다고 해석할 수 있습니다. 매우 직관적이고 단순한 해석입니다. 이제 표준화 계수로 해석을 해보겠습니다. 거실 사이즈가 1 표준편차만큼 커지면 주택가격이 1 표준편차$$0.6773 US dollar 오른다. 이게 도대체 무슨 뜻일까요? 이를 이해하려면 독립변수와 종속변수의 표준편차를 먼저 알아야 합니다.

\[거실사이즈 표준편차= 918 \; feet^2, \; 주택가격 표준편차= 367127 \; USD\]

위의 두 표준편차를 이용해서 다시 해석해보면, 거실사이즈가 918 feet² 커지면 주택가격은 248655 USD (=367127$$0.6773) 오른다. 무슨 뜻인지 쉽게 이해가 되시나요? 전혀 감이 잡히지 않습니다. 왜냐하면 이런 단위는 우리가 평소 잘 사용하는 단위도 아니고 쉽게 이해될만한 사이즈가 아니기 때문입니다. 그렇다면 왜 이런 복잡한 표준화계수를 사용하는 것일까요? 몇 가지 이유는 있습니다. 일단 각 독립변수의 단위를 없애기 위해 각 독립변수의 표준편차를 단위로 사용했다는 점이 그렇습니다. 문제는 단위가 없어져서 동일한 선상에서 비교가 가능하기는 한데, 이 동일한 선상이라는 것이 바로 독립변수의 표준편차들이 됩니다. 우리가 일반적으로 각 변수의 표준편차를 머릿속으로 이해하면서 변수간의 관계를 분석하지 않기 때문에 사실상 현실성이 떨어지는 것이 문제라고 할 수 있습니다.

그렇다면 이제 왜 표준화계수가 필요한지 잠깐 살펴보겠습니다.

첫번째는 논리적으로 영점 즉 (0, 0)을 지나가야 하는 경우입니다. 예를 들어보겠습니다. 경제학에서는 개인의 수입과 지출의 관계를 분석하는 경우가 종종 있습니다. 그래서 개인들의 수입과 지출 데이터를 수집하여 이를 회귀분석으로 분석합니다. 다음과 같은 그림을 보면 이해하실 수 있을 겁니다.

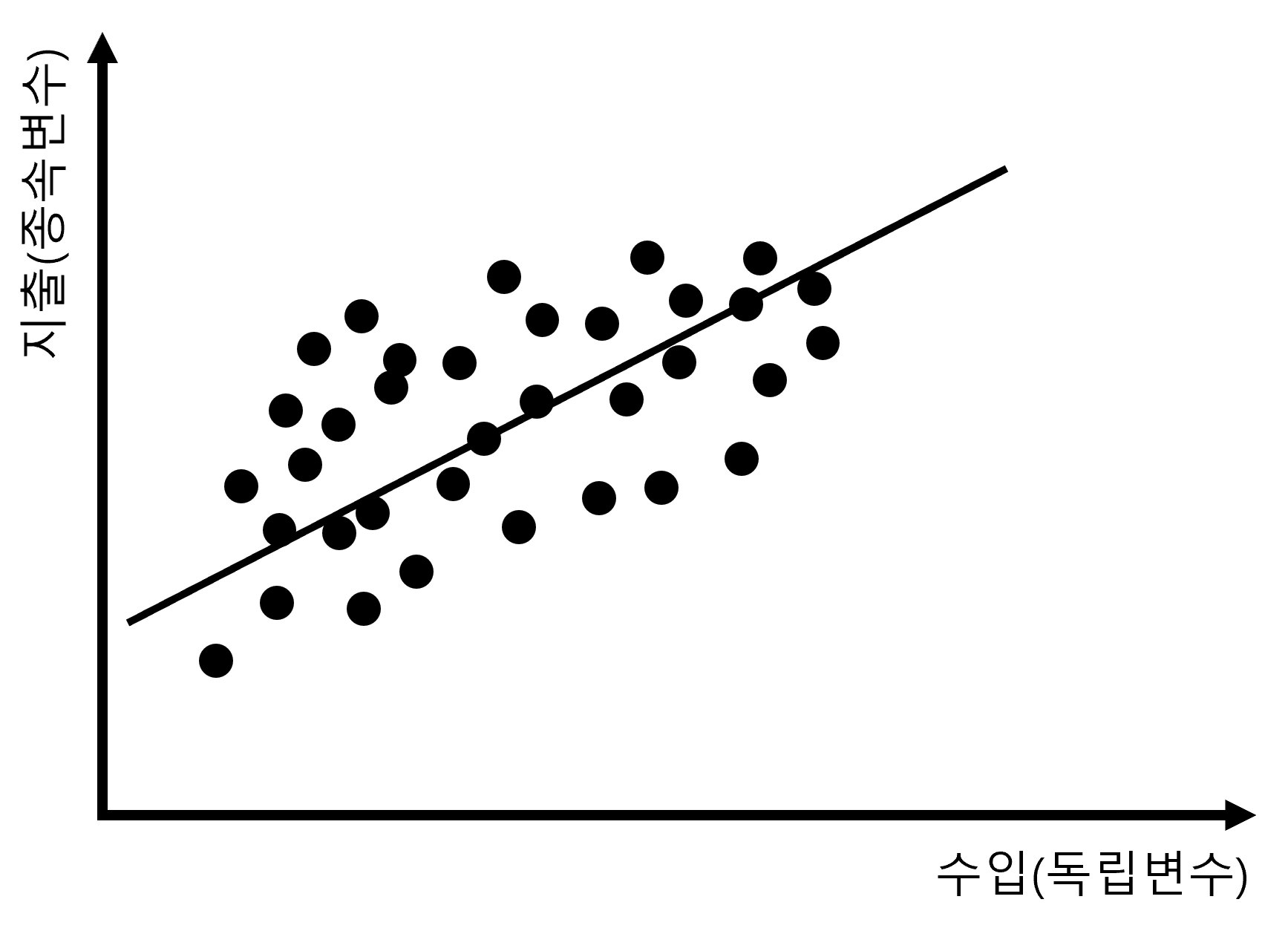
그런데, 문제는 Figure 2.26 에서 보듯이, 이 회귀직선이 대부분 0점을 지나지 않습니다. 왜 그럴까요? 위의 결과만 보면 수입이 없어도 지출이 있다는 의미가 됩니다. 물론, 돈을 빌릴 수도 있고, 다른 도움을 받아서 지출을 할 수도 있기는 합니다. 그러나 그런 특수한 상황은 연구의 대상에서 제외되기 마련입니다. 이와같은 결과가 나오는 이유는 일반적으로 우리가 수집 가능한 데이터에는 수입이 0인 사람이 없기 때문입니다. 문제는 그렇다고 이렇게 내버려둘 수는 없다는 것이지요. 그래서 강제로 회귀직선이 0을 지나도록 하는 방법을 사용할 수 밖에 없습니다. 그게 바로 표준화계수입니다.

표준화계수를 사용하는 두 번째 이유는 앞서 이야기한 것처럼 사용된 여러개의 독립변수 중에서 가장 영향력이 큰 변수를 찾기 위해서 사용합니다. 문제는 앞서 이야기 했듯이 어떤 변수가 영향력이 더 크다 혹은 작다를 결론 내리려면 그에 맞는 통계적 검정을 거쳐야 한다는 것입니다. 따라서 크기가 비슷비슷한 표준화계수들 중에서 누가 조금 더 크다고 해서 해당 변수의 영향력이 가장 크다고 하는 것은 통계적으로 문제가 있는 해석이라는 것입니다. 따라서 너무 단정적으로 해석하는 것은 매우 위험하다고 할 수 있습니다. 더구나 설문조사의 경우 대부분 5점 혹은 7점척도로 통일되어 사용하는 경우가 많아 굳이 표준화를 해야할 필요도 없는 경우가 많습니다. 문제는 표준화계수가 무엇이고 어떻게 계산이 되고 어떻게 사용되어 해석되어야 하는지 자세한 내용은 알지 못하면서 다른 사람들이 이렇게 쓰니 나도 쓴다라는 식의 사용이 문제가 되는 것입니다.

이제 우리는 회귀분석에 대해 조금 더 많이 알게 되었습니다. 조금더 앞으로 나아가 봅시다.

Youtube 바로 가기

2.7 더미변수의 활용

2.7.1 더미변수란 무엇인가?

회귀분석을 공부하다 보면 자연스럽게 더미변수라는 것을 만나게 됩니다. 더미변수는 어떤 변수가 두 개 이상의 범주로 나뉘어진 경우에 사용하는 변수입니다. 예를 들어, 성별을 예로 들어보겠습니다. 성별은 남성과 여성으로 나뉘어지는데, 이를 회귀분석에 사용하려면 어떻게 해야 할까요? 성별을 0과 1로 표현하는 것이 일반적입니다. 그러면 남성은 0, 여성은 1로 표현하면 됩니다. 이렇게 하면 남성과 여성을 구분할 수 있게 되는 것입니다. 물론 반대로 코딩을 할 수도 있습니다. 남성을 1, 여성을 0으로 표현하는 것도 가능합니다. 여기서 무엇이 정답이냐고 묻는 경우가 있느데 사실 정답은 없습니다. 모두 가능합니다. 다만, 분석의 목적이나 해석의 편의성에 따라 선택하면 됩니다. 이제 좀 더 자세하게 알아보겠습니다.

앞에서 우리는 표준화계수를 설명하면서 하나의 모델을 만들어 회귀분석을 했습니다. 앞의 예제를 다시 보면 다음과 같습니다.

종속변수: 주택가격(price)
독립변수
- sqft_living: 거실 사이즈
- floors: 주택의 층수
- waterfront: 물가(강/바다)에 근접한 주택인지의 유무
  - 더미변수(1: 있음, 0: 없음)

여기서 waterfront라는 변수가 더미변수였습니다. 더미란 영어로 Dummy로 씁니다. 더미변수의 특징을 정리해 보면 다음과 같습니다.

값이 오직 0과 1로만 이루어진 변수이며,
값 0과 1에는 수리적인 의미가 없습니다
기본적으로 이산형/범주형 변수인데 이 변수를 연속형 변수처럼 사용하고자 만듭니다
다르게 표현하자면, 더미변수는 범주형 변수를 연속형 변수로 변환하는 방법입니다
더미변수를 사용하면 범주형 변수의 각 범주에 대한 회귀계수를 구할 수 있다는 것이 장점입니다

그렇다면, 왜 더미변수를 사용하는 것일까요?

범주형 변수의 경우 그 범주의 개수가 만약 3개 이상일 경우
- 코딩할 때, 1, 2, 3, 이런식으로 하면 변수의 속성이 연속형 변수가 되어 문제가 발생합니다
- 그러므로 이런 방식으로는 회귀분석에서 사용할 수 없습니다
  - 예제: 학력변수의 경우 중졸/고졸/대졸/석사/박사의 5개 범주를 1/2/3/4/5로 코딩할 경우, 이는 연속형 변수로 인식됩니다
  - 따라서, 여러개의 더미변수를 만들어 사용하는 것이 방법입니다

2.7.2 더미변수를 만들어 보자

이제 더미변수를 만들어 봅시다. 지금 만드는 더미변수는 앞의 ANOVA에서 실습했던 데이터의 일부이기도 합니다.

변수명: payment method
변수의 범주의 개수: 4개
- Bank transfer/credit card/electronic check/mailed check
필요한 변수의 개수 = 범주의 개수 - 1 = 4 - 1 = 3개의 더미변수가 필요함

이게 무슨 뜻인지 잘 이해가 되지 않을 것입니다. 아래의 표를 보면서 이해해 봅시다.

Table 2.1: 더미변수 만들기 예제

	credit card dummy	electronic check dummy	mailed check dummy
bank transfer	0	0	0
credit card	1	0	0
electronic check	0	1	0
mailed check	0	0	1

Table 2.1 을 보면, 첫번째 행에 세 개의 더미변수(credit card, electronic check, mailed check)가 있습니다. 그리고 첫번째 열에는 네 개의 범주가 있습니다. 먼저, 이 세 개의 더미변수는 bank transfer를 기준으로 만들어진 것입니다. bank transfer가 기준이라는 것의 의미는 모든 세 개의 더미변수에서 bank transfer는 0으로 표현되어 있다는 의미입니다. credit card는 오직 credit card dummy에서만 1로 표현되고, electronic check와 mailed check는 0으로 표현되어 있습니다. 동일하게 electronic check은 오직 electronic check dummy에서만 1이고 나머지 credit card와 mailed check은 0입니다. 마지막으로 mailed check은 오직 mailed check dummy에서만 1이고 나머지는 모두 0입니다.

중요한 것은 여기서 각 더미변수가 의미하는 것을 이해하는 것이 중요합니다. credit card 더비면수가 의미하는 것은 bank transfer를 기준으로 credit card가 1이라는 뜻입니다. 이것이 회귀분석에서 의미하는 것은 이 더비변수의 회귀계수가 의미하는 것이 바로 기준인 bank transfer를 기준으로 했을 때, credit card가 회귀계수만큼 차이가 난다라는 의미입니다. 다소 난해할 수 있는데 회귀분석 결과표를 보면서 다시 설명하겠습니다.

아마도 누구나 질문할 만한 것이 바로 왜 bank transfer 더미변수는 없냐는 것일 겁니다. 즉, 범주가 4개이면 더미변수도 4개가 되어야 하는 것이 아닌가 하는 의문을 가질 수 있습니다. 만약 이렇게 범주의 개수와 동일한 개수의 더미변수를 사용하게 되면 회귀분석은 에러가 나거나 통계 소프트웨어가 자동으로 임의의 한 범주를 제거하고 결과를 리포트할 것입니다. 이렇게 범주의 개수와 동일한 개수의 더미변수를 쓰는 것을 더미트랩이라고 하는데, 이렇게 되면 회귀분석이 되지 않습니다. 이유는 이 경우 비교할 기준이 없기 때문입니다. 4개의 범주를 상호간 비교해야 하는데, 이 경우 비교의 대상이 없다면 비교자체가 불가능하기 때문에 에러가 납니다. 물론 수리적으로 해석하면 다른 이야기가 될 것이지만 초보자인 우리는 이정도만 알면 됩니다. 즉, 범주의 개수에서 한 개 뺀 개수의 더미변수를 사용하는 것이 올바른 방법이라는 것입니다.

2.7.3 더미변수를 해석하는 방법

이제 우리가 위에서 만든 세 개의 더미변수를 넣어서 간단한 회귀분석을 하겠습니다. 사용될 독립변수는 이 세 개의 더미변수이고 종속변수는 총 지불금액입니다. 참고로 여기서 사용하는 데이터는 미국의 데이터로 개인이 인터넷을 사용하는 경우 지불하는 지불 방법에 따라서 총 지불금액이 같은지 다른지 알아보겠다는 의도를 가지고 실시한 회귀분석입니다.

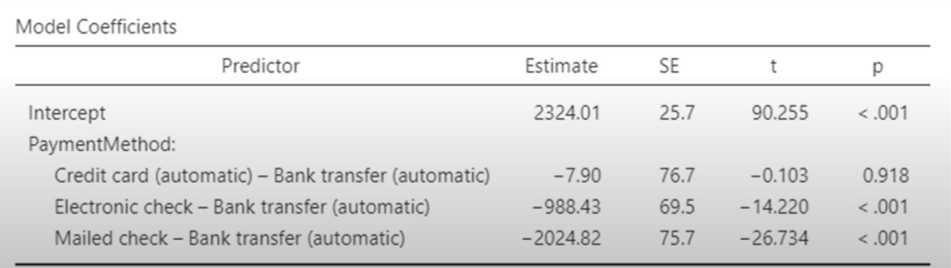
Figure 2.27 는 회귀분석 결과표입니다. Jamovi는 다른 소프트웨어보다 꽤 친절하게 결과를 리포트해 줍니다. 우선, 우리가 사용한 더미변수에서 기준이 되는 범주는 bank transfer입니다. 이 범주는 더미변수로서 추가되지 않고 모든 더미변수에서 0으로 코딩되어 기준그룹 (reference group)이 됩니다.

그럼 위의 결과표를 해석해 보겠습니다. 첫번째 줄의 intercept는 상수 혹은 절편입니다. 다음 줄의 PaymentMethod라는 줄이 세 개의 더미변수를 모아 놓은 것입니다. 첫번째가 Credit card 더미변수입니다. Jamovi에서는 기준그룹이 누구인지 분명하게 알려주기 위해 Credit card - Bank transfer 이런 식으로 표기합니다. 뒤의 Bank transfer는 기준그룹이라는 의미입니다. 첫번째 더미의 Estimate는 회귀계수이고 그다음의 SE는 표준오차, t는 t-value, p는 p-value입니다. 우선 확인해야 할 것은 Credit card 더미의 p-value가 0.918이므로 유의하지 않다는 것입니다. 이것이 의미하는 것은 Credit card의 총지불금액과 Bank transfer의 총지불금액이 통계적으로 유의하게 다르지 않다는 의미입니다. 즉, 동일하다는 것이지요. 우리말로 조금 쉬게 풀어보면, 신용카드로 지불하는 고객과 계좌이체를 하는 고객의 인터넷 사용료 총 지불금액이 통계적으로 동일하다는 것입니다. 즉, 아무런 차이가 없다는 것입니다.

두번째는 Electronic check 더비변수입니다. 이 더미변수의 p-value는 0.001보다도 작다고 되어 있으므로 통계적으로 유의합니다. 주의해야할 것은 회귀계수의 방향(+/-)입니다. Electronic check의 회귀계수는 -988.43입니다. 이는 전자수표로 지불하는 고객과 계좌이체로 지불하는 고객의 총지불금액이 통계적으로 유의한 차이가 있고, 전자수표로 지불하는 고객이 계좌이체하는 고객에 비해 평균적으로 988.43 US Dollar 적은 총지불금액을 보인다는 의미입니다. 중요한 것은 단순히 유의하다가 아니라 기준그룹에 비해 해당 범주가 얼만큼 차이가 크다 혹은 작다를 분명하게 해석해야 한다는 점입니다.

마지막으로 Mailed Check 더미변수는 통계적으로 유의하면서 회귀계수가 -2024.82임을 확인할 수 있습니다. 이는 종이수표로 지불하는 고객이 계좌이체를 하는 고객에 비해 평균적으로 2024.82 US Dollar 적게 지불하고 있다는 것을 의미합니다.

이와같이 더미변수는 범주형 변수를 마치 연속형 변수인것 처럼 바꾸어 회귀분석에 독립변수로 넣어 쉽게 해석할 수 있다는 장점이 있습니다. 그런데 만약 연구자가 Electronic check와 Mailed check를 비교하고 싶다고 하면 현재의 더미변수로는 비교가 불가능합니다. 왜냐하면 현재 비교대상이 되는 기준그룹이 바로 Bank transfer이기 때문입니다. 따라서, 이렇게 비교하고자 하는 범주가 다를 경우 기준그룹을 그 범주로 변경하여 다시 더미변수를 만들어 회귀분석을 해야합니다.

더미변수는 알고나면 매우 단순하지만, 정확하게 이해하지 못하면 제대로 활용하지 못하는 아쉬움이 많은 변수입니다. 정확하게 알고 잘 사용하도록 합시다.

Youtube 바로 가기

2.8 다중공선성 (Multicollinearity)이란 무엇일까?

2.8.1 발음도 어려운 단어 다중공선성

사실 한글로도 발음이 어렵긴합니다만, Multicollinearity는 미국 아이들도 발은에 꽤 애를 먹는 그런 영어단어입니다. 보통 회귀분석을 공부해보신 분이라면 많이 들어본 단어일 것입니다. 이를 이해하기 위해서는 기본적으로 상관관계, R²의 계산, 그리고 최소제곱법에 대한 개념은 알고 있어야 합니다.

2.8.2 그림으로 이해하는 다중공선성

여태까지는 단순하게 독립변수가 1개인 회귀분석만 공부했습니다. 하지만 현실적으로 독립변수가 1개인 회귀분석은 사실상 의미가 없습니다. 요즘은 거의 보기 어렵긴합니다만, 불과 몇 년전까지만해도 단 1개의 독립변수로 회귀분석을 하는 논문이 꽤 있었습니다. 재미있는 것은 이런 회귀분석을 다른 독립변수로 여러개 만들어 리포트하는 방식이 상당히 많았다는 점입니다. 뒤에가서 설명할 일이 있겠지만, 이런 방법은 거의 100% Model Mis-specification 즉 모형 부적합으로 보아야 합니다. 하나의 종속변수를 설명하는 인과관계에 있는 독립변수가 단 1개일 수는 없기 때문입니다. 결론적으로 모델을 너무 심하게 단순화했다고 보는 것이지요.

어쨋든 이번에는 독립변수가 3개인 회귀분석을 생각해 봅시다.

\[y = a + b_1 x_1 + b_2 x_2 + b_3 x_3\]

위와 같은 회귀식이 있다고 합시다. 앞서 이야기 했듯이 회귀분석이란 종속변수의 분산을 독립변수로 설명하는 것이라고 했습니다. 이를 그림으로 그려보면 다음과 같습니다.

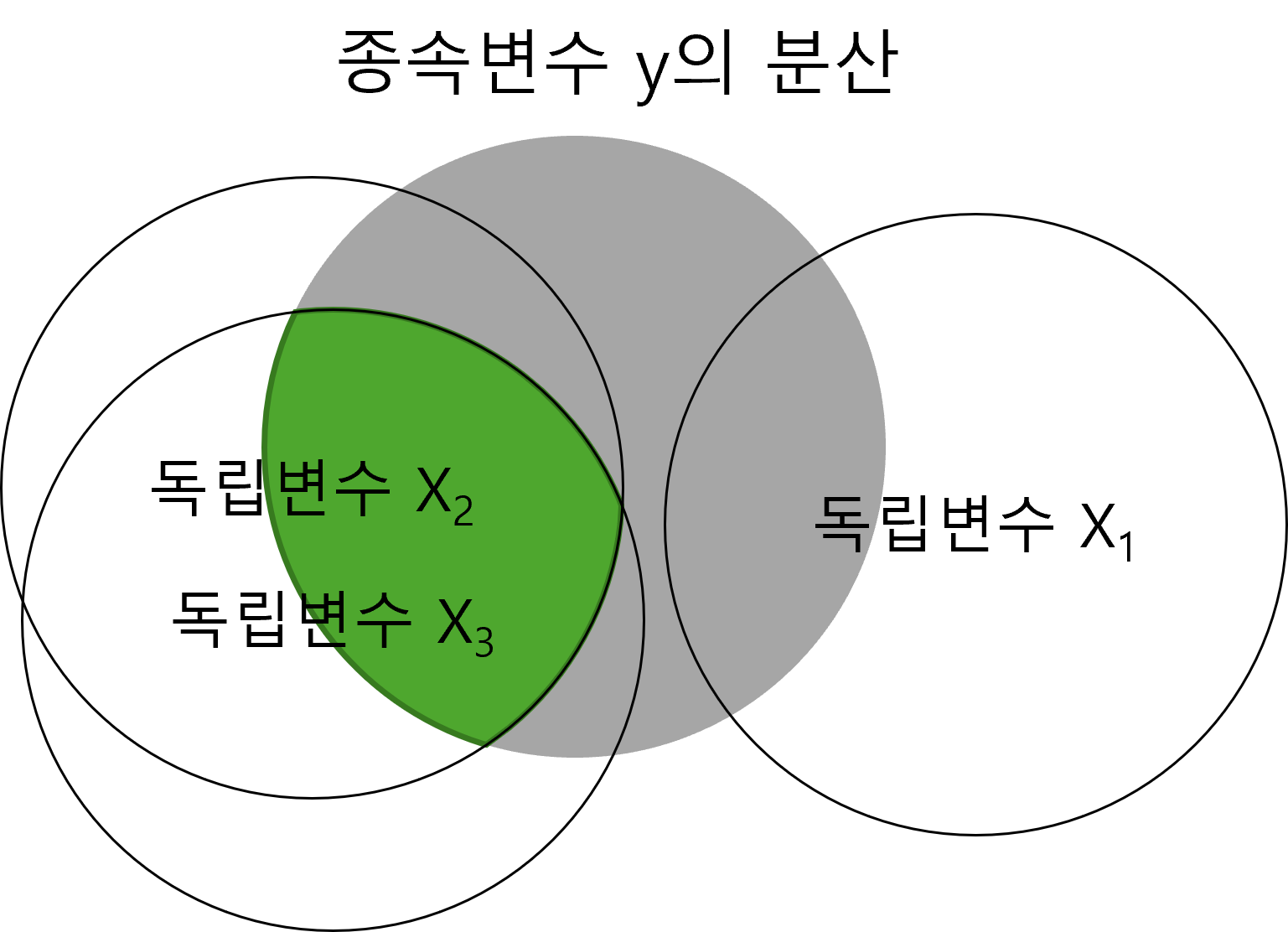
회색 동그라미 부분이 종속변수 y의 분산입니다. 이 분산을 우리는 세 개의 독립변수로 설명하려 합니다. 문제는 독립변수 $x_2$와 $x_3$이 서로 상관관계가 높다는 것입니다. 이는 두 독립변수가 서로 설명하는 종속변수의 분산이 겹치는 것을 의미합니다. Figure 2.28 을 보면 $x_2$와 $x_3$이 서로 상관관계가 높아 종속변수 y의 분산을 설명하는데 중복되는 부분이 많다는 것을 알 수 있습니다. 이를 다중공선성이라고 합니다.

2.8.3 왜 다중공선성이 문제일까?

다중공선성은 회귀분석에서 큰 문제입니다. 이유는 다음과 같습니다.

만약 두 변수가 완벽한 다중공선성에 걸려 있다면, 다르게 말해 $x_1 = b_2 x_2$ 라고 하면,
이는 회귀분석에서 $x_1$과 $x_2$가 동일한 변수로 취급된다는 것을 의미합니다
이렇게 되면, 회귀분석의 가정(전제조건)을 위배하는 것이며, 이런 경우 회귀분석은 불가능합니다
왜냐하면, 같은 변수를 두 번 넣은 것이기 때문에 최소제곱법 계산이 불가능하기 때문입니다

그렇다면, 완벽한 다중공선성, 영어로는 perfect collinerity가 아니어도 문제가 될까요?

그렇습니다. 이런 경우 회귀계수의 표준오차가 비정상적으로 커지는 것이 문제입니다
표준오차의 비정상적 확대가 왜 문제일까요?
- 회귀계수값의 유의성은 t-value에 의해 결정됩니다
- 앞에서 살펴본 것처럼, t-value는 회귀계수를 표준오차로 나눈 값입니다
- 그러므로, 다중공선성으로 인해 표준오차가 비정상적으로 커지면 t-value값이 작아져서 유의해야할 변수가 유의하지 않게 되어
- 회귀분석의 결과를 왜곡하게 됩니다

2.8.4 다중공선성을 확인하는 방법

다중공선성을 확인하는 방법은 여러가지가 있습니다. 가장 대표적인 방법은 다음과 같습니다.

산포도 & 상관계수

두 독립변수의 산포도를 보았을 때, 심각하게 상관관계가 높아보인다면 다중공선성이 의심됩니다
이런 경우 상관계수를 확인할 필요가 있습니다
- 상관계수가 만약 0.9를 넘는다면 (0.9보다 작아도) 다중공선성의 문제가 있을 수 있습니다

허용공차 (tolerance)를 확인

Tolerance란 한 개의 독립변수를 종속변수로 놓고 나머지 독립변수를 독립변수로 하는 회귀분석을 했을 때 나오는 R²를 이용해 (1-R²)로 계산한 값입니다
만약, R² 가 1 이라면 이는 독립변수 간에 심각한 상관관계가 있음을 의미합니다
- 이 경우 tolerance인 (1-R²)는 0이 될 것이므로
- Tolerance가 0이면 완벽한 상관성을 의미하여 다중공선성이 심각함을 의미합니다

분산팽창지수 (VIF: Variance Inflation Factor)

가장 많이 사용하는 방법으로,
$VIF = 1 \div tolerance = 1 \div (1-R^2)$
그러므로, VIF가 크다는 것은 다중공선성이 크다는 의미가 되며
일반적으로 VIF가 10보다 크면 문제가 있다고 판단합니다
그러나 이는 연속형변수의 경우에 해당합니다
만약 더미변수의 경우에 VIF가 3 이상이라면 다중공선성을 의심해야 합니다

상태지수 (Condition Index)

흔하게 사용되지는 않는 방법입니다
일반적으로 100 이상이면 심각한 다중공선성이 존재한다고 봅니다

2.8.5 다중공선성을 해결법

다중공선성이 큰 변수가 유의한지 아닌지 확인해야 합니다

대부분의의 경우 변수를 무조건 빼라고 하는데 그렇지 않습니다
다중공선성이 있음에도 불구하고 만약 주요 관심심 독립변수가 유의하다면 그 변수를 빼는 것은 좋지 않습니다
- 이는 표준오차가 비정상적으로 팽창되었음에도 유의하다는 뜻이기 때문에 이 변수가 그럼에도 불구하고 매우 유의하다는 의미가 되어 그대로 두어도 무방합니다
- 간혹 여기에 태클을 거는 사람들이 있는데, 100% 완벽한 다중공선성이 아닌 한 문제가 크게 되지는 않습니다
특히나, 조절효과를 확인하기 위해 교호작용(interaction) 변수를 추가하는 경우 연구자가 의도적으로 interaction을 추가하여 어느 정도의 다중공선성을 피할 수는 없습니다
따라서, 약간의 다중공선성 문제가 발생하더라도 연구자의 의도와 변수의 유의성에 따라 결정해야 합니다

해당 변수를 제거

가장 일반적인 방법으로,
문제는 해당변수가 연구의 중심이되는 중요변수일 경우 문제가 됩니다
만약 중요변수라면, 다른 변수를 제거하거나 변수를 변형하여 다중공선성을 해결해야 합니다
문제는 이러한 방법이 불가능하다면 경우에 따라서 연구 자체가 망가져 버릴 수 있습니다
대부분의 경우, 이러한 문제가 발생하는는 근본적인 원인은 기존연구 및 이론/논리적 구성이 사전에 부족했기 때문입니다

주성분분석으로 변수를 재조합

뒤에서 공부할 주성분분석은 변수간의 겹치는 분산을 제거하는 효과가 있습니다
이렇게 중복되는 분산을 제거하면 VIF 문제는 쉽게 해결되지만,
문제는 반드시 중복되는 분산만 제거하는 것은 아니어서 경우에 따라 재조합된 변수가 이상한 결과를 내는 경우가 많습니다

다중공선성이 발생한 독립변수들을 합친다

다중공선성이 높은 (상관관계가 높은) 변수들은 결국 비슷한 것을 의미하므로,
이들을 하나로 합쳐서 회귀분석에 사용할 수 있습니다
그러나, 새로 합쳐 놓은 변수가 유의하다 해도 해석이 애매하거나 어려워질 수 있습니다
또한, 이러한 방법은 변수가 많을 경우에는 적용하기 어렵습니다
왜냐하면 많은 변수를 하나로 합치면 이 변수가 의미하는 바가 모호해지기 때문입니다
하나로 합치는 방법으로는 평균값을 가장 많이 사용하나 이것도 완벽하다고 할 수는 없습니다

능형 회귀분석

이런 회귀분석 방법이 있다고 알고만 일단 넘어갑시다
최근에 많이 관심을 받는 방법이기는 하나 초보자에게는 어려운 방법입니다

Mean centering 방법

모든 변수를 각 변수의 평균값으로 뺀 뒤에 회귀분석을 하는 방법
어느정도의 효과는 있으나 완벽하지는 않으며,
최근 연구에 따르면 이 방법은 전혀 효과가 없다고 합니다
문제는 이 방법이 국내에서는 상당히 많이 사용되고 일종의 미신처럼 여겨지고 있습니다

이제 회귀분석의 기본적인 내용들을 거의 다 마스터 해가고 있습니다. 조금만 힘내서 끝가지 가보도록 합시다.

Youtube 바로 가기

2.9 이분산성이란 무엇인가?

이분산성(Heteroscedasticity)은 회귀분석에서 오차항의 분산이 일정하지 않은 경우를 의미합니다. 이분산성이 발생하면 회귀분석의 가정이 깨지게 되어 회귀분석 결과가 신뢰할 수 없게 됩니다. 이분산성이 발생하면 회귀분석 결과에 대한 통계적 검정이 신뢰할 수 없게 되며, 회귀분석 결과의 예측력이 떨어지게 됩니다.

일반적으로는 위와 같이 설명을 합니다. 무슨 뜻인지 쉽게 이해가 되지 않지요? 그렇다면 하나씩 알아보겠습니다.

2.9.1 이분산성의 의미

이분산성은 영어로 Heterodascity라고 합니다. Hetero는 다양한, 다른이라는 뜻이 있습니다. 반대말은 Homo입니다. 그러므로, 이분산성이란 분산이 다르다는 의미입니다. 그렇다면 누구의 분산이 다르고 이게 왜 문제가 되는 것일까요?

누구의 분산이 다른가? - 회귀분석에 투입된 독립변수의 회귀계수 표준오차(분산)이 다르다는 의미입니다

왜 문제일까? - 회귀계수의 유의성을 판단하려면 우선 t-값을 계산해야 하는데 - t-value는 회귀계수를 표준오차로 나눈 것이므로 - 표준오차가 이분산성을 띄게되면 하나의 수로 나타낼 수 없습니다 - 왜냐하면 표준오차가 독립변수의 값에 따라서 변하기 때문입니다

2.9.2 이분산성의 예제

앞의 회귀분석 예제를 이용해 보겠습니다.

종속변수: 주택가격 (price)
독립변수: 거실크기 (sqft_living)

한 개의 독립변수를 사용하여 회귀분석을 하기 전에, 독립변수를 x축으로 종속변수를 y축으로 하는 산포도를 그려보겠습니다

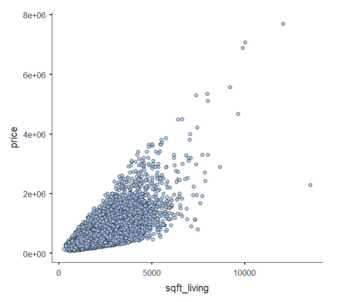
Figure 2.29 의 산포도를 보면 sqft_living의 값이 커질 수록 price의 폭이 점점 커지는 것을 볼 수 있습니다. 이 데이터로 회귀분석을 하면 다음과 같습니다.

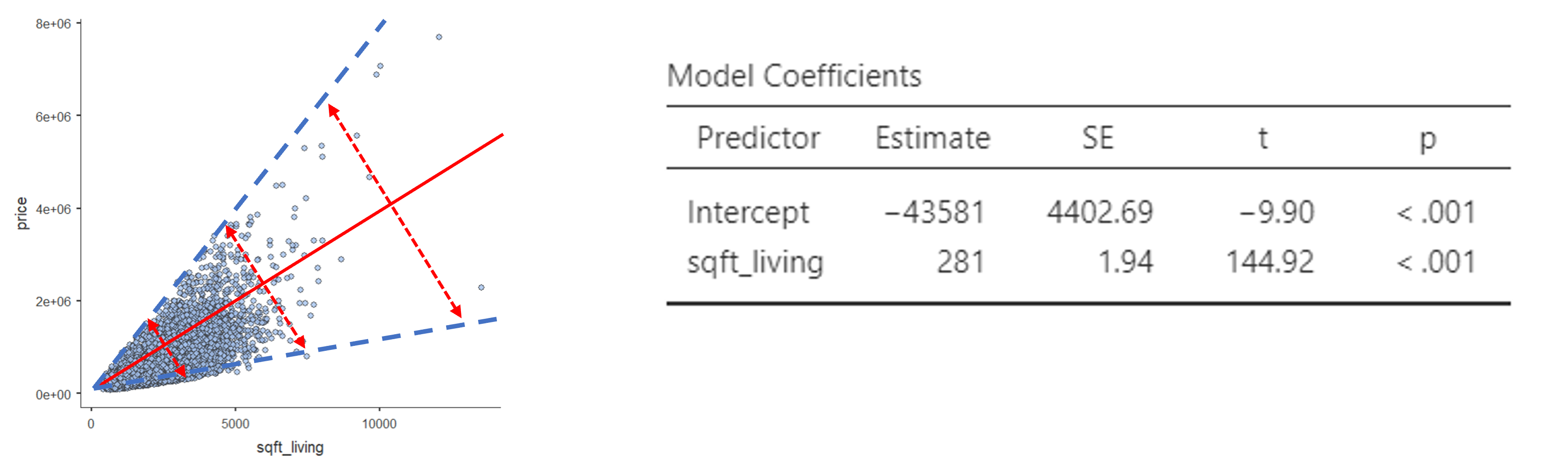
Figure 2.30 의 회귀분석 결과를 보면 sqft_living의 회귀계수는 281이며, 이 회귀계수는 통계적으로 유의합니다. 그러나, 이 회귀계수의 표준오차는 1.94로 나타나 있지만 좌측의 그림에서 보듯이 sqft_living이 커질 수록 price의 폭이 커지기 때문에 이 표준오차값을 신뢰할 수 없게 됩니다. 확실하게 확인하려면 잔차도를 확인해 보면 알 수 있습니다.

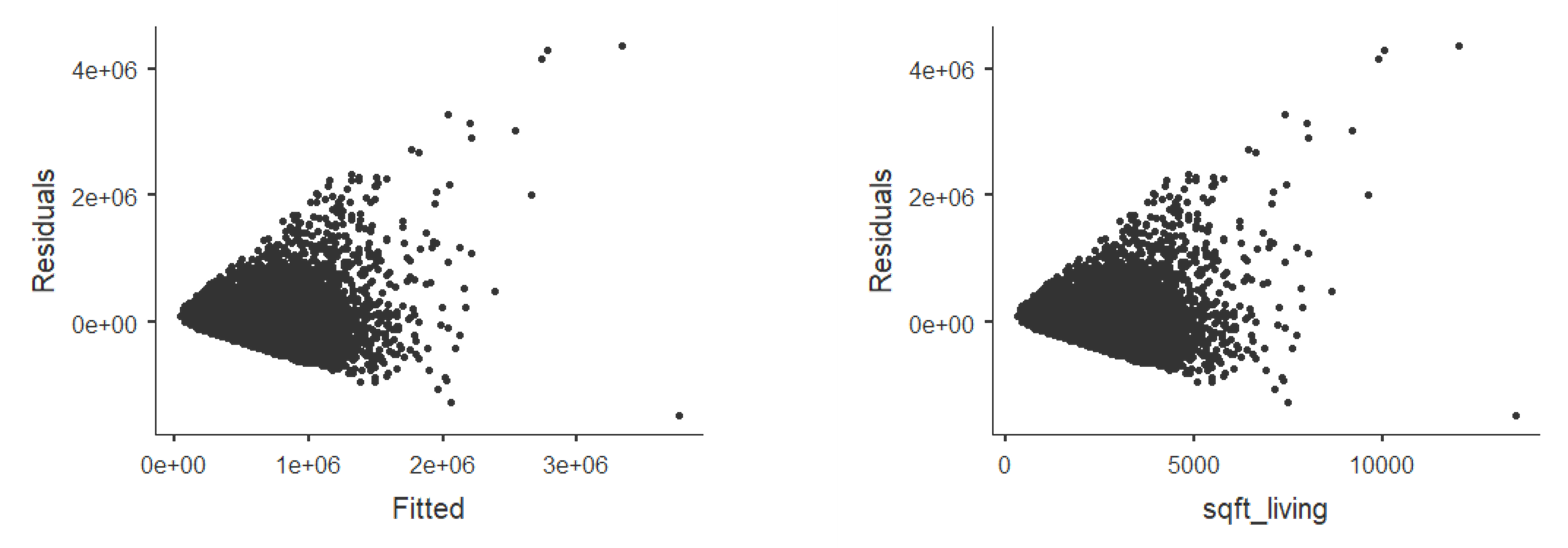
Figure 2.31 의 잔차도를 보면 sqft_living이 커질 수록 잔차의 폭이 커지는 것을 볼 수 있습니다. 이것이 이분산성이 발생한 것입니다.

2.9.3 이분산성을 확인하는 방법

산포도
잔차도
White test

테스트 결과가 유의하면 이분산성이 있다는 뜻

Goldfeld-Quandt test

테스트 결과가 유의하면 이분산성이 있다는 뜻

Breusch-Pagan test

테스트 결과가 유의하면 이분산성이 있다는 뜻

주로 사용하는 방법은 White test와 Breusch-Pegan test입니다.

2.9.4 이분산성의 해결책

(heteroskdastistic) robust standard error를 사용

구하는 방법은 너무 복잡함
통계 프로그램에 따라서 기능을 제공하기도 하고 아니기도 함

Weighted least square regression (WLS regression)

이분산성의 모형을 모델링하는 함수를 찾아서 그 역함수로 독립변수를 만들어 추가하는 OLS
문제는 이분산성의 함수를 찾는다는 것이 쉽지 않음
이론적으로는 쉬우나 현실적으로는 어려움

GLS/FGLS regression

근본적으로는 WLS와 동일한 개념으로 접근
이론적으로는 쉬우나 현실적으로는 어려움

이러다 보니 불과 몇 년전까지만 해도 이분산성이 발견되면 연구를 접어야 하나 고민하기도 했습니다. 최근에는 워낙 소프트웨어가 좋아져서 Robust standard error를 클릭 한 번으로 구해주는 프로그램이 많아졌습니다. 이러한 프로그램을 사용하실 것을 권합니다.

Youtube 바로 가기

2.10 회귀분석을 실습해 보자

이제 회귀분석을 실습해 보도록 하겠습니다.

사용할 테이터와 변수는 다음과 같습니다.

Data: House sales price in Kings County, USA (Kaggle.com에서 다운로드 가능)
종속변수: price (= 매매 가격)

우리가 앞에서 공부한 내용들을 바탕으로 진행하는 실습입니다. 동영상을 보면서 차근차근 따라해 보시길 바랍니다.

데이터 다운로드가 어려우신 분들은 여기서 다운로드 받으시기 바랍니다.

Youtube 바로 가기

2.1 회귀분석이란 무엇인가?

2.1.1 회귀분석이란?

2.1.2 회귀분석의 예제

2.2 결과표를 해석하자

2.2.1 회귀분석의 예제 데이터와 연구가설

2.2.2 회귀분석 결과표의 해석

2.3 회귀분석과 표준오차

2.3.1 표준오차란 무엇일까?

2.3.2 표준오차의 정의

2.4 회귀분석과 t-test

2.4.1 왜 t-test일까?

2.4.2 회귀분석과 t-test의 비교

2.4.3 회귀분석에서 주의할 점

2.5 R2를 어떻게 해석해야 할까?

2.5.1 통계의 의미와 R2

2.5.2 높은 분산설명력과 낮은 분산설명력

2.5.3 애증의 R2

2.5.4 회귀분석과 잔차도

2.6 회귀분석의 표준화계수

2.6.1 표준화계수를 알고 사용할까?

2.6.2 표준화계수의 예제

2.6.3 표준화계수의 계산방법

2.6.4 표준화계수의 해석

2.7 더미변수의 활용

2.7.1 더미변수란 무엇인가?

2.7.2 더미변수를 만들어 보자

2.7.3 더미변수를 해석하는 방법

2.8 다중공선성 (Multicollinearity)이란 무엇일까?

2.8.1 발음도 어려운 단어 다중공선성

2.8.2 그림으로 이해하는 다중공선성

2.8.3 왜 다중공선성이 문제일까?

2.8.4 다중공선성을 확인하는 방법

2.8.5 다중공선성을 해결법

2.9 이분산성이란 무엇인가?

2.9.1 이분산성의 의미

2.9.2 이분산성의 예제

2.9.3 이분산성을 확인하는 방법

2.9.4 이분산성의 해결책

2.10 회귀분석을 실습해 보자

2.5 R²를 어떻게 해석해야 할까?

2.5.1 통계의 의미와 R²

2.5.3 애증의 R²