3 분산분석 (ANOVA)

3.1 이제 다시 시작해 보자

3.1.1 새로운 시작은 아는 것에서 부터

이제 우리는 통계의 첫 관문을 통과 했습니다. z-test와 t-test가 무엇인지 알게 되었고 이를 jamovi라는 통계 프로그램을 통해 분석할 수 있게 되었습니다.

축하드립니다!!!

별 것 아닌 것 같아도 사실 여러분들은 굉장히 크고 의미 있는 한 걸음을 내딛은 것입니다. 통계를 공부하는 사람들이 대부분 여기까지 하고 다음부터는 그냥 SPSS같은 프로그램을 따라 하기 바빠집니다. 그러다보니 나중에 어떤 통계 결과표를 보고서도 해석 하는 못하고 그저 유의하다는 말만 반복하게 되는 것입니다. 사실 통계를 공부하는 학생들을 이렇게 만드는 그 원인은 아마도 분산분석 (ANOVA) 때문일 것입니다. 어떻게든 t-test까지는 알듯 말듯 하면서 힘겹게 공부해서 진도를 나갔는데, 그 다음에 만나는 것이 바로 분산분석입니다. 여기부터는 정말이지 도통 알 수 없는 말들의 향연이자 그냥 계산하고 결과보고 유의한지 아닌지만 알게 되는 상황이 됩니다. 그래서 대부분의 통계를 공부하는 분들이 분산분석에서 통계를 포기하기에 이릅니다.

하지만 저는 여러분들에게 포기하지 말라고 말씀드리고 싶네요. 아직 포기하기엔 이릅니다. 저와 함께 이제 한 발자국 더 통계의 세계로 여행을 떠나 봅시다. 그렇다고 무조건 쉽게 알려드리겠다는 장담을 하지는 않겠습니다. 다만 앞에서도 그랬듯 최대한 여러분들이 이해하기 쉽게 차근차근 나아가겠습니다.

이제 우리가 시작할 분산분석은 영어로 ANOVA라고 합니다. 이 ANOVA라는 단어는 줄임말입니다. 정확하게는 Analysis of Variance의 약자입니다. 영어를 해석해 보면 말 그대로 분산분석입니다. 자, 그럼 이제 분산분석의 시작점을 잡아야 합니다. 분산분석의 시작점은 우리가 앞서 배운 t-test입니다. 그러면 복습도 할 겸 다시 t-test의 정의를 살펴보겠습니다.

모집단의 표준편차가 알려지지 않았을 때, 정규분포의 모집단에서 모은 샘플(표본)의 평균값에 대한 가설검정 방법

위의 정의를 이제는 조금 이해하시겠지요? 사실 그리 쉽게 설명한 정의는 아니지만 우리는 위에 등장한 모집단, 표준편차, 정규분포, 샘플(표본), 평균값 그리고 가설검정이라는 단어들을 이미 다 공부했습니다. 그러니 천천히 읽고 생각해 보면 그다지 어려운 표현은 아니라는 생각이 들 것입니다. 하지만 너무 어렵게 표현한 것만은 사실입니다. 굳이 이렇게 설명했어야 했나라는 생각은 정말 많이 드네요.

앞서 t-test를 처음 공부할 때, 제가 t-test의 목적을 그냥 이렇게 이해하는 것이 좋다고 이야기 했습니다. “어떤 두 집단이 같은지 다른지 알고 싶을 때 하는 테스트.” 그렇습니다. 좀 쉬운 그러나 너무 단순화한 t-test의 목적이기는 합니다. 하지만 핵심적인 내용을 명확하고 쉽게 담고 있는 정의입니다.

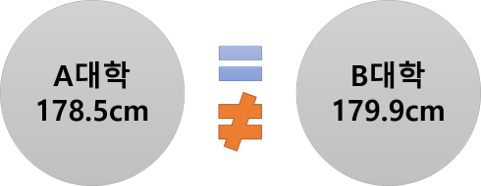
그래서 우리는 앞서 A와 B라는 두 대학교의 남학생의 평균키가 같은지 다른지 알아보고자 하는 t-test를 진행하였습니다. 여기서 우리는 두 대학의 남학생의 키가 동질적인지 아닌지 알고 싶었습니다. 이 목적을 달성하기 위해 t-test를 했던 것이지요. 그런데, 만약에 다음과 같이 우리 동네에 대학교가 하나 더 있다고 가정하면 우리는 이제 세 개의 대학의 남학생의 평균키가 같은지 다른지 알고 싶은 상황이 됩니다. 이렇게 되면 어떻게 해야 할까요?

3.1.2 꼼수의 대마왕

사실 인간은 잔머리를 잘 씁니다. 쉽게 말해 꼼수의 대마왕이지요. 우리는 여태 힘들게 t-test를 배웠고 이제 막 한 숨 돌리던 차였습니다. 그런데 갑자기 우리 앞에 분산분석이 나타나니 마음 한편이 좀 불편했을 수 있습니다. 이렇게 되고 나니, 저 세 개의 그룹을 비교하려고 할 때 우리는 새로운 분산분석을 배우려 하기 보다는 기존에 알던 t-test를 이용해 어떻게든 새로운 공부를 피해보고 싶기 마련입니다. 그래서 처음에 누구나가 생각하는 방법이 바로 이것입니다.

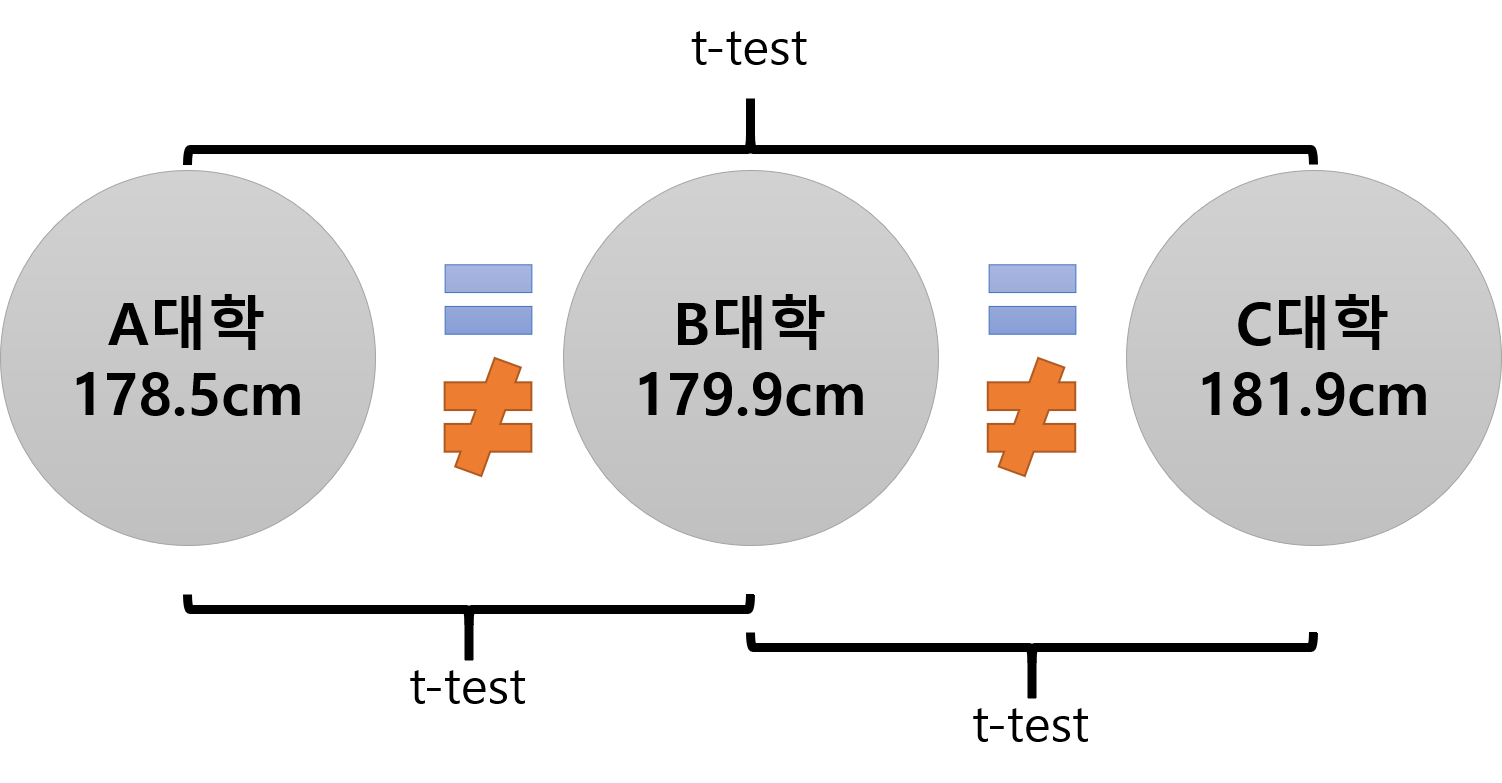
우리는 이것을 Multiple t-test라고 부릅니다. 즉, t-test를 여러 번 한다는 의미가 됩니다. 이 예를 Multiple t-test로 해결하려면 일단 A대학과 B대학을 t-test로 비교해서 B대학 남학생이 키가 더 크다고 나오고, 두 번째로 B대학과 C대학을 t-test로 비교하여 B대학 보다는 C대학이 크다고 나오고, 마지막으로 이를 A대학과 C대학을 t-test로 비교하여 확실히 A대학보다 C대학의 남학생 키가 크다고 나오면 우리는 이 세 번의 t-test 결과를 종합하여 이렇게 결론 내릴 것입니다. A대학 \(\leq\) B대학 \(\leq\) C대학 이런 식으로 말입니다.

어떤가요? 그럴듯하지요? 뭐 이렇게 보면 굳이 분산분석이라는 새로운 방법을 배울 필요가 없어 보입니다. 그런데 말입니다. 그럴 리가 있나요. 세상 그렇게 단순하지 않습니다. 이 Multiple t-test에는 한 가지 심각한 문제가 있습니다. 여기서 등장하는 것이 앞서 배웠던 1종 오류입니다. 기억나시나요?

3.1.3 1종 오류의 재등장

다시 한 번 이야기 하자면, 1종 오류란 귀무가설이 실제로는 참인데, 연구결과 귀무가설이 기각되어 거짓이라고 나오는 상황입니다. 예를 들어 어떤 치료제가 실제로는 아무 효과가 없는데, 연구결과 이 치료제가 효과가 있다고 나타난 경우입니다. 그렇다면 이 1종 오류가 여기에서 왜 등장할까요? 먼저 우리는 1종 오류(\(\alpha\))에 대해서 다시 떠 올려야 합니다. 앞서 \(\alpha\)를 유의수준이라고 부른다고 했고 이 유의수준을 5%로 정한다고 이야기 했습니다. 즉, 우리가 일반적으로 말하는 p값의 기준인 5%가 다른 한편으로는 1종 오류를 5%로 제한하겠다는 의미라는 것이지요. 즉, 우리의 분석결과가 아무리 잘 못 되었다 하더라도 1종 오류가 발생할 가능성이 5%보다는 낮다는 것을 의미합니다.

이제 다시 multiple t-test로 돌아가 봅시다. 우리는 세 번의 t-test를 진행하였고 이 세 번의 t-test의 결과를 종합하여 “A대학 \(\leq\) B대학 \(\leq\) C대학”라는 결론을 도출했습니다. 그리고 이 세 번의 t-test에서 매 번 우리는 자연스럽게 5%의 유의수준 (\(\alpha\))를 사용했습니다. 문제는 우리가 5%의 유의수준 (\(\alpha\))를 세 번 사용하여 이를 종합하여 결론을 내렸기 때문에 우리가 이 분석에서 실제로 사용한 유의수준은 5%가 아닌 약 15%가 됩니다. 왜냐하면 5%를 세 번 사용했으니 대략 3을 곱하면 15%가 되는 것입니다.

물론 정확한 유의수준을 구하는 공식은 다음과 같습니다.

\[\alpha_{FW} = 1- (1-\alpha)^c \approx \alpha \times c \]

위의 공식에서 c는 Multiple t-test를 몇 회 하였는지를 의미합니다. 결국 앞서 우리가 이야기 했듯이 이 값은 대략 사용된 유의수준에 테스트 횟수를 곱한 값과 유사합니다. 따라서 위의 예제의 경우 우리는 나름대로 5%의 유의수준을 기준으로 테스트했다고 생각했지만 실제로는 15%의 유의수준을 가지고 테스트한 것이 되었으므로 1종 오류의 가능성이 분명히 생긴 것입니다. 결론적으로 말하자면 그룹이 3개 이상인 경우 t-test를 여러 차례 시행하는 Multiple t-test는 불가 하다는 것입니다. 그러니 우리는 싫어도 분산분석을 배워야 하겠네요.

이제 우리는 분산분석을 공부해야 하는 이유를 알았습니다. 그러면 다시 마음을 잡고 새로운 통계의 세계로 여행을 떠나 봅시다!!!

YouTube 바로 가기

3.2 ANOVA 말고 변수

3.2.1 본격적인 시작 전에 알아야할 그것, 변수

이제 우리는 ANOVA를 공부해야만 한다는 사실을 알았습니다. Multiple t-test로 어떻게 해보고 싶었지만 안 되기 때문입니다. 분산분석을 시작하기 전에 우리는 변수에 대해 알아보고 갈 것입니다. 만약 변수에 대해 잘 알고 있다면 그냥 넘기셔도 됩니다. 우리가 공부할 내용은 다음의 것들입니다.

독립변수
종속변수
통제변수

그럼 이제 하나씩 시작해 봅시다.

3.2.2 독립변수

굳이 통계가 아니어도 독립변수라는 이름은 많이 들었을 것입니다. 아무 생각 없이 들으면 그냥 그러려니 할 수도 있지만, 가만히 생각해보면 이름이 참 독특합니다. 독립변수. 도대체 무엇으로부터 독립인 것일까요? 책이나 인터넷을 찾아보면 다음과 같이 설명이 되어 있습니다.

독립변수: 연구자/조사자가 의도적으로 변화시키는 변수 혹은 다른 말로 예측변수(predictor variable) 또는 설명변수(explanatory variable)

여기서 독립이란 것이 무슨 뜻일까요? 독립변수라고 할 때의 독립이 의미하는 것은 논리적 관계성에서의 독립을 의미합니다. 일반적으로 우리는 변수를 이용해 논리적 인과관계를 연구하거나 다루게 됩니다. 이러한 인과관계에서 독립적인 위치를 가진 변수가 독립변수입니다. 인과관계에서 독립적인 위치란 원인과 결과의 관계에서 원인을 의미합니다. 왜냐하면 결과는 원인에 의해 영향을 받거나 좌우되기 때문에 독립적일 수 없기 때문입니다. 따라서 독립변수란 인과관계에서 원인이 되는 변수라고 이해하면 보다 쉽습니다.

다만, 위에 책이나 인터넷에 나온 것처럼 연구자/조사자가 의도적으로 변화시킬 수 있다고 하여 이 독립변수를 연구자가 마음대로 바꿔도 된다는 의미가 아닙니다. 어디까지만 독립적인 변화가 가능하고 이러한 독립적인 변화를 이용하여 연구자나 조사자가 연구/조사를 진행할 수 있다는 의미입니다. 의도적이라는 말에 너무 의미를 두게 되어 마치 조작이 가능하고 더 나아가서 조작하거나 마음대로 바꿔도 된다고 이해하는 것은 매우 위험합니다.

3.2.3 종속변수

종속이란 단어는 사실 일상생활에서는 많이 사용하는 단어는 아닙니다. 종속이란 어딘가에 속해 있다. 정확하게는 주가 되거나 강한 힘을 가진 어떤 것에 좌우되는 것을 의미합니다. 여기서 말하는 주가 되거나 강한 힘을 가진 어떤 것이 앞에서 이야기한 독립변수이고 이 독립변수에 의해 좌우되는 것이 바로 종속변수입니다. 책이나 인터넷을 찾아보면 이런 설명이 되어 있습니다.

종속변수: 연구자/조사자가 독립변수의 변화에 따라 어떻게 변하는지 알고 싶은 변수 혹은 다른 말로 반응변수(response variable) 또는 결과변수(outcome variable)

그러므로 여기서 말하는 종속은 논리적 인과관계에서의 종속을 의미합니다. 따라서 원인과 결과의 관계에서 종속에 해당하는 것은 결과이고 이 결과를 의미하는 변수가 종속변수입니다. 종속변수는 우리가 연구에서 알고 싶은 주요한 대상이자 결과입니다. 이 결과를 어떻게 하고 싶을 때 우리는 이 결과에 영향을 미칠만한 독립변수를 이용해 독립변수의 변화에 따라 종속변수가 어떻게 되는지 연구하는 것입니다. 다음의 Figure 3.4 에서 보면 고등교육이라는 변수는 독립변수이고 임금수준의 상승은 종속변수입니다. 일반적으로 경제학에서는 대학교육과 같은 고등교육을 투자로 인지합니다. 왜냐하면 상당한 돈과 시간을 투자하여 졸업 후 상당한 수준의 임금상승을 기대하는 행위이기 때문입니다. 따라서 고등교육을 받았기 때문에 임금이 높다는 것은 논리적 인과관계에서 이상이 없습니다. 중요한 것은 많은 연구자들이 이렇게 단순한 논리적 인과관계는 무시한 채로 아무 변수나 독립변수에 혹은 종속변수에 넣어서 분석하는 경우가 많다는 것입니다. 논문 심사를 하다 보면, 인과관계가 전혀 없거나 심지어 인과관계가 바뀌어 원인과 결과를 뒤집어서 논문을 발표하는 학생을 가끔 봅니다. 큰 일이 아닐 수 없습니다. 대부분 지도교수의 지도를 무시하고 단행한 경우 발생하는 일입니다. 연구 전에 충분히 읽어보고 생각하여 논리적 인과관계에 대해 확신을 가지고 연구를 진행해야 합니다. 의외로 이런 경우가 많습니다.

3.2.4 통제변수

보통은 Control variable이라고 하는 변수입니다. 기본적인 역할은 독립변수와 동일합니다. 즉, 종속변수에 영향을 주는 변수입니다. 그러나 이 변수는 독립변수의 역할을 하면서도 사실상 주인공이라기보다는 조연에 가깝습니다. 그렇다고 무시하거나 없으면 안 되는 존재입니다. 예를 들면, 어느 식당의 재방문율을 종속변수로 하고 고객만족을 독립변수로 하는 연구/조사를 진행한다고 가정합니다. 이런 경우, 가장 많이 하는 실수가 단 하나의 독립변수만으로 종속변수에 대한 영향을 확인하는 것입니다. 이게 왜 문제가 되냐 하면, 종속변수인 재방문율에 영향을 미치는 중요한 변수는 오직 고객만족 하나일리는 없기 때문입니다. 고객만족 말고도 예를 들어 음식의 맛이나 서비스의 품질, 혹은 인테리어 등의 분위기 등이 중요한 변수일 수 있습니다. 만약 이런 중요한 통제변수를 제외하고 단 하나의 독립변수만으로 분석을 하게 되면, 이 하나의 변수가 다른 모든 변수들을 대표하게 되어 문제가 됩니다. 일반적으로 이런 상황을 Model mis-specification 이라고 부릅니다. 즉 모형이 잘못되었다는 의미가 됩니다.

현재 우리가 공부하는 분산분석은 단 한 개의 독립변수만을 가지고 분석하는 일원배치 분산분석(One-way ANOVA)입니다. 물론 그렇다고 일원배치 분산분석은 다 잘못된 것이라는 의미는 아닙니다. 그러나 보다 현실적이고 깊이 있는 연구/조사를 하고자 한다면 상당한 수준의 중요한 변수들을 통제변수로 포함하여 분석하는 것이 좋습니다. 우리가 앞으로 공부할 통계적인 방법 중에 이런 것들이 있을 것입니다.

이제 슬슬 보다 본격적인 분산분석을 공부해 봅시다.

YouTube 바로 가기

3.3 ANOVA 전에 알아야 할 것들

3.3.1 일원배치 분산분석의 독립/종속변수

우선 우리가 지금 배우는 것은 일원배치 분산분석입니다. 일원배치라는 말은 저도 참 이해가 어렵기는 합니다만 영어로는 One-way로 번역합니다. 여기서 One-way가 의미하는 것은 독립변수가 한 개라는 것입니다. 그러므로 Two-way ANOVA는 이원배치 분산분석이 되고 여기서는 독립변수가 두 개가 됩니다. 중요한 것은 모든 분산분석에서 독립변수와 종속변수는 동일한 특징이 있다는 점입니다. 이것이 바로 우리가 분산분석을 공부하기 전에 알아야 하는 것입니다.

분산분석에 사용되는 변수의 특징
- 종속변수: 연속형 변수 (Continuous variable)만 가능함
- 독립변수: 이산형(Discrete variable) 혹은 범주형 변수(Categorical variable)만 가능함

위에서 이야기하는 변수의 종류가 무엇인지 잘 모르겠다면 앞부분의 Section 1.5.3 을 다시 공부해보시기 바랍니다.

예를 들어 보겠습니다. 아주 오래전에나 가능했던 것이지만, 예전에는 연구윤리라는 개념이 없었던 시절이 있었습니다. 당시에 영상물이 어린이들의 폭력성에 미치는 영향을 연구하고자 어린 아이들을 세 그룹으로 나누어 한 그룹에는 폭력적인 영화장면을, 다른 그룹에는 드라마를, 마지막 그룹에는 공익광고를 보여준 뒤에 이 아이들을 관찰실에 들여보낸 후 아이들이 관찰실에서 보이는 폭력적인 행동을 점수화 하였습니다. 생각해보면 사람을 상대로 그것도 어린 아이들을 상대로 이런 실험을 실제로 했다는 것이 믿기지 않지만, 과거에는 이런 일들이 일어나기도 했습니다.

하여튼, 이 경우 적용되는 분석방법이 바로 분산분석입니다. 그렇다면 위의 예에서 독립변수와 종속변수는 무엇인지 설명해 볼까요?

종속변수: 점수화된 아이들의 폭력성
독립변수: 세 가지 종류의 영상(폭력영화/드라마/공익광고)

좀 이해가 되시나요? 그렇다면 다른 예를 들어보죠. 신종플루 치료제를 개발 중인 어느 제약회사에서 신종플루 감염자를 대상으로 신약의 효과를 측정하고자 합니다. 이 경우 종속변수와 독립변수는 어떤 식으로 만들어질까요?

종속변수: 신약을 복용한 후 완치까지 걸린 날짜
독립변수: 세 가지 약을 복용한 그룹(개발중인 신약/기존의 독감약/플라시보)

이 경우 완치까지 걸린 날짜가 종속변수가 됩니다. 반면에 독립변수는 세 가지 그룹이 있을 수 있습니다. 첫 번째 그룹은 개발 중인 신약을 복용한 그룹이고, 두 번째 그룹은 기존의 독감약을 복용한 그룹입니다. 이 두 그룹을 비교하는 것은 충분히 이해가 됩니다. 기존 독감약에 비해 개발 중인 신약이 어느 정도의 효과인지 비교할 수 있겠지요. 마지막의 플라시보는 무엇일까요? 보통 위약이라고도 부릅니다. 위약효과라는 표현도 있죠. 간단하게 말해 아무 효과도 없는 밀가루 덩어리를 약처럼 만들어서 먹이는 겁니다. 즉, 아무것도 처치하지 않은 그룹이죠. 이 그룹은 사람의 자연적인 면역력으로 치료가 되는 기간을 측정하는 것입니다. 물론 현실에서는 매우 위험하고 윤리적인 문제가 있습니다. 어디까지나 하나의 예로서 든 것뿐입니다.

또 다른 예를 들어보겠습니다. 이 예는 나중에 우리가 직접 통계 소프트웨어를 이용해 분석할 문제이기도 합니다.

만약 어느 인터넷 서비스 기업 (ISP: Internet Service Provider)이 자신의 고객들의 총 지불금액이 고객별 이용대금 지불방법에 따라 차이가 있는지 알고 싶다면 종속변수와 독립변수는 어떻게 될까요?

종속변수: 총 지불금액 (Total charges)
독립변수: 대금 지불방법 (총 4가지 그룹)
- 계좌이체 (Bank transfer)
- 신용카드 (Credit card)
- 전자수표 (Electronic check)
- 종이수표 (Mailed check)

3.3.2 ANOVA를 위한 데이터 코딩

이번에는 엑셀에 데이터 코딩하는 것과 관련해서 잠깐 설명하고자 합니다. 갑자기 웬 데이터 코딩이냐고 하시겠지만 이게 용어가 워낙 오래된 것이라서 안 쓸 수도 없고 그러네요. 요즘에는 코딩이란 말이 프로그래밍이란 말과 혼용되어 사용되지만 사실 데이터 분석에서 코딩이란 말은 데이터를 입력하는 것을 의미합니다. 지금이야 온라인으로 설문조사를 하고 그 결과가 자동으로 엑셀에 입력되지만 과거에는 종이로 설문지를 만들어 돌리고 그 결과를 책상 한편에 쌓아 두고 한 부 한 부 정성스럽게 엑셀에 입력해야 했습니다. 이 작업을 코딩이라고 불렀지요. 지금도 그렇기는 합니다만, 요즘은 이렇게 종이로 받은 설문지를 직접 코딩하는 경우가 많지는 않지만 여러분이 스스로 통계 조사와 분석을 하려면 당연히 알아야 합니다. 왜냐하면 이걸 잘 못해서 혹은 몰라서 분석 자체를 시작도 하지 못하는 경우가 많기 때문입니다.

아래의 Figure 3.5 를 보면 코딩이 완료된 엑셀 화면에서 한 개의 행(row)는 관찰값(observation)을 의미합니다. 여기서 관찰값이란 예를 들면 설문조사를 했을 경우 한 명의 설문 응답자의 응답을 의미합니다. 동일한 한 명의 사람이 응답한 결과는 한 개의 행(row)에 입력되는 것입니다. 그러므로 만약 100명의 사람들에게서 설문 응답을 받아 이를 제대로 코딩했다면 100개의 행(row)을 갖게 되는 것입니다.

다음은 동일한 엑셀 화면에서 한 개의 열(column)을 보여주고 있는 Figure 3.6 입니다. 엑셀에 코딩된 화면에서 한 개의 열(column)은 한 개의 변수를 의미 합니다. 지금 화면에는 모든 변수를 다 보여주고 있지 못하지만 결론적으로 열(column)의 개수를 세어보면 우리는 데이터의 변수의 개수를 알 수 있다는 의미 입니다. 사실 이 엑셀화면은 나중에 우리가 실습에 사용할 데이터입니다. 이 데이터의 종속변수와 독립변수를 확인해 보도록 하겠습니다.

아래의 Figure 3.7 과 Figure 3.8 을 확인해보면 종속변수와 독립변수를 알 수 있습니다. 종속변수는 보다시피 연속변수이고 독립변수는 4가지 그룹의 범주형 변수입니다. 잘 안보일 수도 있으나 종속변수는 숫자라는 점 그리고 독립변수는 문자로된 4가지 그룹으로 되어 있다는 점입니다. 중요한 것은 독립변수의 4가지 그룹이 한 개의 열(column)에 있다는 점입니다. 경우에 따라 초보자들은 이 독립변수를 한 개의 열(column)이 아닌 4개의 열(column)에 입력하는 실수를 하기도 합니다. 이렇게 되면 아예 분석이 불가능합니다. 꼭 기억하기 바랍니다. 한 개의 변수는 한 개의 열(column)에 입력되어야 한다는 사실 말입니다.

3.3.3 엑셀 코딩시 편리한 기능

사실 이런 방법은 저도 원래는 제 학생들에게만 알려주는 것인데 공개하는 내용입니다. 알고 보면 정말 별 것 아니지만 아는 것과 모르는 것이 편리하기가 천지차이이기 때문입니다. 본래 엑셀에서 엔터키를 누르면 커서가 아래쪽 방향으로 이동합니다. 문제는 앞서 이야기 했듯이 우리가 코딩할 때, 한 명의 응답자의 응답을 입력하려면 한 개의 열(row)에 입력해야 합니다. 1번 질문에 대한 답을 3이라는 값으로 입력하고 난 후에 엔터를 치면 커서가 우측이 아닌 아래로 내려갑니다. 이렇게 되면 우리는 방향키를 이용해서 커서를 다음 입력위치로 옮겨 놓아야 합니다. 매우 번거로운 일입니다.

이 문제를 해결하는 방법은 매우 쉽습니다. 엑셀에서 <파일> 메뉴를 클릭한 뒤에 <옵션>을 클릭하고, 그 후에 <고급>을 눌러보시기 바랍니다. 가장 상단에 엔터키를 누른 후 커서의 이동방향을 설정할 수 있는 부분이 있을 것입니다. 기본 값은 아래쪽으로 되어 있지만 이 방향을 우측으로 변경한 뒤에 저장 후 다 시 엑셀을 실행해 보면 엔터키를 치고 난 뒤에 커서가 우측으로 움직이는 것을 확인하실 수 있을 것입니다. 알고 보면 정말 별것 아니지만 수백 장의 설문지를 코딩하는 경우 상당한 시간을 아낄 수 있습니다.

더불어 위의 경우와 같이 독립변수의 그룹을 문자열로 입력할 경우 일부 통계 프로그램은 이를 인식하지 못하는 문제가 발생합니다. 즉, Bank transfer, Credit card, Electronic check, Mailed check과 같은 문자열은 인식이 안 되어 이를 강제로 1, 2, 3, 4로 바꿔 코딩해야 하는 경우가 있습니다. 이 경우 기존의 변수를 지우지 말고 엑셀에서 추가로 열(column)을 생성해서 여기에 엑셀의 if 함수를 사용해 변경해 주는 것이 빠르고 편리합니다. 대부분의 통계 프로그램에서 이를 변경하려고 하면 오히려 시간과 노력이 더 많이 들어가는 경우가 많기 때문입니다. 다만, 우리는 이런 수고를 할 필요가 없습니다. 왜냐하면 우리가 사용할 Jamovi라는 프로그램은 위의 문자열을 알아서 범주형 변수로 인식하기 때문입니다. 매우 편리한 기능이 아닐 수 없습니다.

그럼 이제 분산분석에 대해 본격적으로 배워봅시다!!

YouTube 바로 가기

3.4 ANOVA의 기본을 이해하자

3.4.1 책에 등장하는 Equation

다시 한 번 강조하자면 우리가 하는 것은 일원배치 분산분석 (One-way ANOVA)입니다. 이 분산분석의 목적은 세 개 이상의 그룹을 비교하고자 할 때 하는 것입니다. 이유는 두 개의 그룹을 비교할 때 사용 하던 t-test를 여러 번 해서 이 결과들을 종합하여 결론을 내릴 경우 우리는 문제가 된다는 것을 앞서 배웠기 때문입니다. 우리가 하려는 것은 바로 Figure 3.2 의 그림과 같은 상황입니다.

이제 보통 통계를 공부하다가 통계책에서 이런 것을 발견하곤 합니다.

\[Y_{ij} = \mu \;+\; \tau_{j} \;+\; \epsilon_{ij} \] \[Y_{ij} \;-\; \mu = \tau_{j} \;+\; \epsilon_{ij} \]

이게 무엇일까요? 보통 굳은 결심으로 통계책을 펴고 공부를 시작해도 이런 것을 보게 되면 많은 경우 통계를 반쯤 포기하게 됩니다. 여러분들은 그럴 필요가 없습니다. 제가 도와드리겠습니다. 위의 것은 그냥 어려워 보이게 써 놓은 것일 뿐 사실 내용을 알고 보면 그다지 어려운 것은 아닙니다.

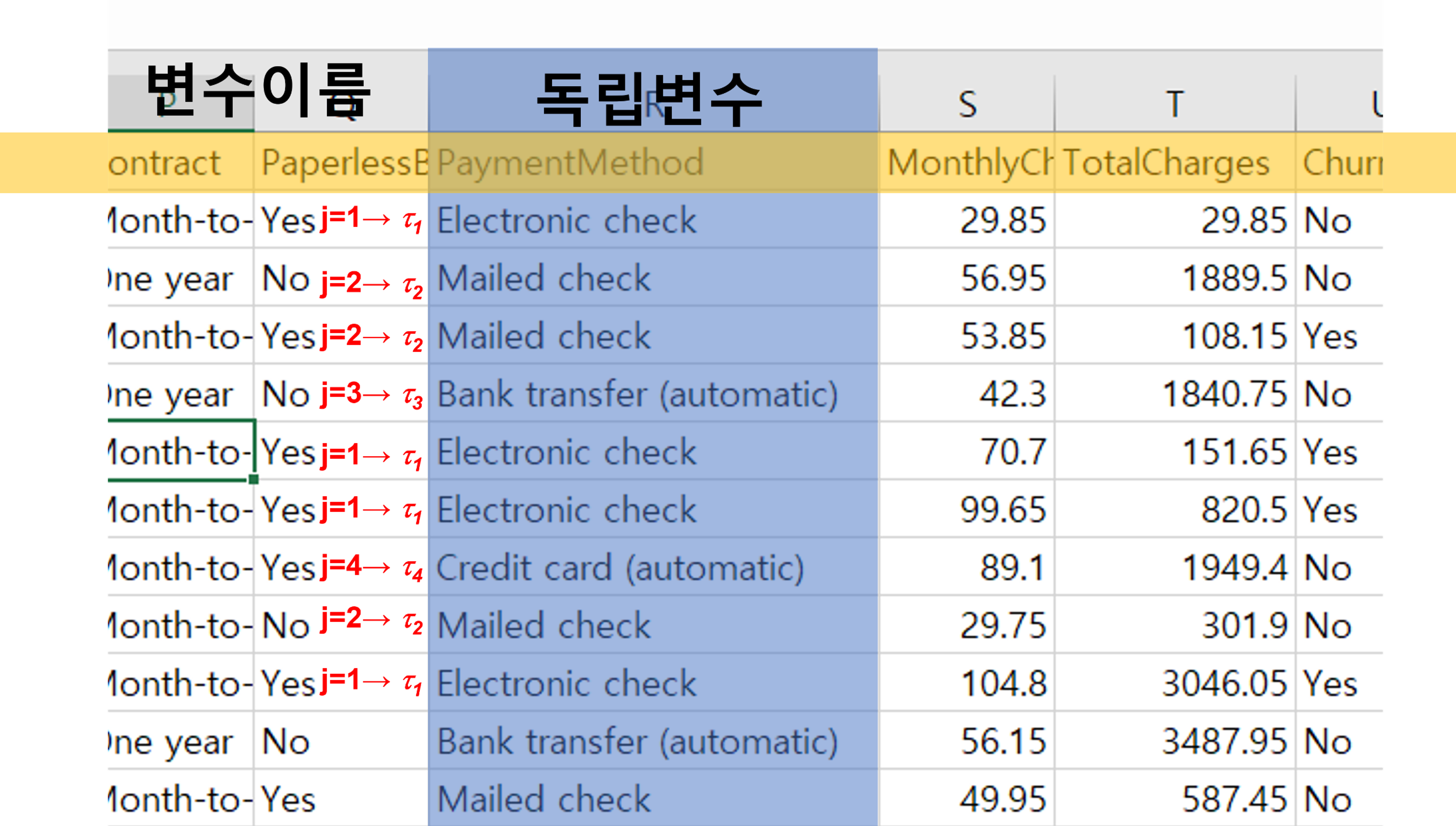
첫 번째 식과 두 번째 식은 같은 식입니다. 다만 \(\mu\) 를 우측에서 좌측으로 옮겨 놓은 것뿐입니다. 기본적으로 \(=\) 기호의 좌측을 좌항 우측을 우항이라고 합니다. 좌항부터 일단 보겠습니다. \(Y_{ij}\) 는 분산분석에서 종속변수를 의미합니다. 앞서 이야기 했듯이 종속변수는 연속변수(continuous variable)이어야 합니다. 기본적으로 대문자 \(Y\)가 종속변수를 의미합니다. 이런 식으로 표현하는 이유는 한 개의 문자를 이용해 데이터의 모든 종속변수에 해당하는 숫자를 표기하기 위함입니다. 마치 중학교 때 배운 미지수 \(x\)와 같은 것입니다. 그렇다면 \(Y\)의 아래에 있는 아래첨자 \(_{ij}\)는 무엇일까요? 기본적으로 \(j\)는 분산분석의 독립변수의 그룹을 의미합니다. 조금 헷갈릴 수 있는데요. 갑자기 종속변수에 독립변수의 그룹을 표기하는 것이 이상해 보일 수 있습니다. 이렇게 생각하면 됩니다. 종속변수에 해당하는 어떤 데이터가 있습니다. 이 데이터는 숫자 즉 연속형 변수인데, 이 숫자가 어느 독립변수의 그룹의 영향으로 만들어진 데이터인지 알기 위해 \(j\)라는 문자를 사용해서 표기하는 것입니다. \(i\)라는 문자는 해당 그룹 내에서 몇 번째 종속변수인지를 의미합니다. 조금 어려우시다고요? 그렇다면 앞에서 보았던 데이터의 엑셀 코딩 화면을 보면서 설명해 보겠습니다.

위의 Figure 3.9 를 보면 독립변수 한 열(column)과 종속변수 한 열(column)을 볼 수 있습니다. 이제 화면을 조금 확대해서 보겠습니다.

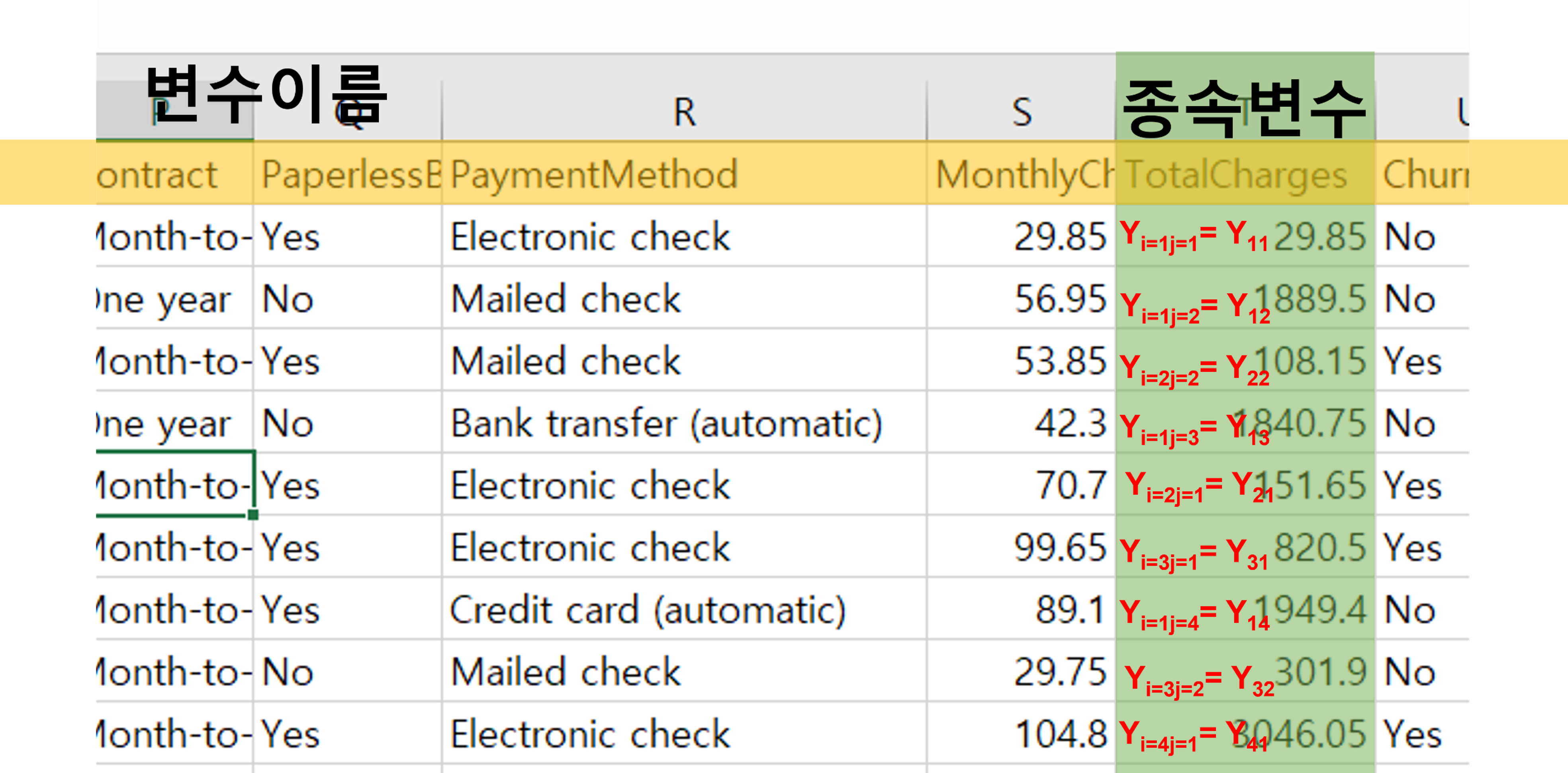
우리가 사용할 종속변수는 Total Charges입니다. 이 변수의 변수명이 첫 번째 행(row)에 있고 그 아래로 종속변수의 값이 쭉 있습니다. 첫 번째 값은 29.85인데요. 그 앞에 앞의 열(column)인 Payment Method가 바로 우리가 사용할 독립변수입니다. 여기서 독립변수는 4 개의 그룹으로 이루어져 있습니다. 예를 들어 Electronic chek을 1번 그룹으로 Mailed check을 2번 그룹으로 Bank transfer (automatic)을 3번 그룹으로 Credit card (automatic)을 4번 그룹으로 지정했다면 이 번호가 바로 위의 공식에 등장 하는 \(j\)값이 됩니다. 그러므로 첫 번째의 29.85라는 값은 1번 Electronic check그룹의 첫 번째 값이므로 \(i=1\), \(j=1\)이 되어 이 값은 \(Y_{11}=29.85\)가 됩니다. 그 아래의 1889.5라는 종속변수의 값은 Mailed check 그룹에 속한 값이므로 \(j=2\)가 되고 이 두 번째 그룹의 첫 번째 값이므로 \(i=1\)이 되어 \(Y_{12}=1889.5\)가 됩니다. 다시 그 아래의 108.15라는 값은 두 번째 그룹인 Mailed check의 두 번째 값이므로 \(i=2\), \(j=2\)가 되어 \(Y_{22}=108.15\)가 됩니다. 이 방식을 계속 적용해보면 그 다음의 값은 \(Y_{13}=1840.75\)가 됩니다. 이는 세 번째 그룹인 Bank transfer (automatic)에 속한 첫 번째 값이라는 의미가 됩니다. 이런 방식으로 모든 종속변수의 값에 고유의 넘버링을 할 수 있습니다. 이게 바로 위에 등장하는 공식의 좌항인 \(Y_{ij}\)입니다.

이제 \(\tau_{j}\)에 대해 알아봅시다. Figure 3.11 에서 독립변수 Payment Method는 네 가지 그룹으로 되어 있습니다. 위에서 설명한 것처럼 Electronic chek을 1번 그룹으로 Mailed check을 2번 그룹으로 Bank transfer (automatic)을 3번 그룹으로 Credit card (automatic)을 4번 그룹으로 지정했습니다. 이 번호가 바로 \(j\) 입니다. 그래서 첫 번째의 Electronic check은 \(\tau_{1}\)이 되고, 두 번째와 세 번째의 Mailed check은 \(\tau_{2}\)가 되고 Bank transfer (automatic)은 \(\tau_{3}\)가 됩니다.

이제 마지막으로 남은 것은 \(\epsilon_{ij}\)입니다. 여기서 \(i\), \(j\)는 종속변수의 경우와 동일합니다. 문제는 이 \(\epsilon\)이 무엇이냐 인데 이것이 의미하는 것은 오차(error)입니다. 갑자기 웬 오차인가 싶을 수도 있겠지만 쉽게 설명하자면 우리가 가진 데이터를 우리의 통계적 모델인 분산분석이 완벽하게 100% 설명할 수는 없습니다. 아주 약간씩의 오차는 있을 수밖에 없는 것이지요. 이것을 의미합니다. 다만 여기서 말하는 오차는 random한 오차입니다. 즉 무작위성의 오차라는 의미입니다. 따라서 이 오차는 큰 의미가 없는 것입니다. 만약에 이 오차가 무작위가 아니라면 기본적으로 우리의 분석 모델이 잘못되었거나 이 오차 안에 뭔가 다른 의미가 있어서 그 의미를 찾아내야 하는 상황이 됩니다. 일단 이런 복잡하고 어려운 상황은 기초적인 단계에서는 다룰 수 없으니 분산분석의 오차는 일단 무조건 random한 오차라고 이해합시다. 이와 관련되어서는 사실 뒤에 나오는 회귀분석에서 보다 자세하게 다룰 일이 있을 것입니다.

자, 그럼 이제 다시 이 두 개의 식을 들여다봅시다.

\[Y_{ij} = \mu \;+\; \tau_{j} \;+\; \epsilon_{ij} \]

\[Y_{ij} \;-\; \mu = \tau_{j} \;+\; \epsilon_{ij} \]

어떤가요? 이해가 되나요? 사실 알고 보면 별것 아닙니다. 위의 식들은 우리의 분산분석을 그리고 우리의 데이터를 일반화해서 써 놓은 것입니다. 궁극적으로 위의 식이 의미하는 것은 그룹별(독립변수) 차이가 종속변수에 나타나는 것인지 아닌지 보겠다는 것입니다. 그러니 이제 통계책에서 이런 복잡해 보이는 식을 만나더라도 너무 긴장하지 말고 절대 통계를 포기하지 말기 바랍니다.

YouTube 바로 가기

3.5 ANOVA는 F-value(F값)이다

3.5.1 분산분석의 F-value

이제 우리는 분산분석을 시작하려 합니다. 사실 앞에서 했던 z-test와 t-test처럼 분산분석도 이런 유의 이름이 있습니다. 바로 F-test입니다. 방금 알게 된 사실인데, 제가 지난 몇 년간 바빠서 유투브 댓글을 거의 보지 못하고 있었습니다. 우연히 조금 전에 들어가 봤더니 많은 분들이 이 F-value의 F는 Fisher의 F라는 것을 댓글로 알려주셨네요. 생각해 보니 너무 당연한 건데 저도 의외로 너무 바보같이 그냥 지나쳤습니다. 사실 유명한 Fisher의 정확검정 같은 것만 생각해봐도 이 ANOVA의 창안자가 Fisher라는 점은 너무 당연하네요. 하여간 그렇답니다. 댓글 달아주신 분들께 감사드립니다. 저도 한 수 배워갑니다.

z-test에 z-value가 있었고 t-test에 t-value가 있었듯이 분산분석인 F-test에는 F-value가 있습니다. 그렇습니다. 분산분석 즉 ANOVA는 F-value가 핵심입니다. 중요한 것은 분산분석의 F-test 역시 앞에서 공부한 z-test나 t-test와 동일한 흐름으로 진행된다는 것입니다. 그럼 앞에서 했던 것들을 잠시 떠 올려 봅시다.

z-test를 다음 위해서 우리는 먼저 z-value를 구하고 이 z-value를 표준 정규분포를 기본으로, z-table (표준 정규분포표)에서 이 값을 찾아서 우리가 원하는 p-value를 구하였습니다. t-test에서는 먼저 t-value를 구하고 역시 t-distribution을 기본으로, t-table에서 앞에서 구한 t-value를 찾아서 우리가 원하는 p-value의 critical value (c.v.)를 알아내었습니다. 그러므로 F-test에서는 먼저 F-value를 구할 것이고 이것을 F-distribution에 기반하여 F-table에서 우리가 원하는 p-value와 관련한 정보를 얻어낼 것입니다. 그러므로 전반적인 프로세스는 동일합니다.

이제 분산분석을 시작해 봅시다.

3.5.2 이름이 왜 분산분석인가?

갑자기 이게 무슨 뚱딴지같은 질문일까 생각하시는 분도 있겠지만, 언제나 우리의 공부의 시작은 바로 질문입니다. 자 생각해 봅시다. 우리가 원하는 것은 정확하게 말하면 세 개 이상의 집단의 평균값이 같은지 다른지 알고 싶다는 것입니다. 에를 들면 Figure 3.2 처럼 말이죠. 앞에서 공부한 t-test는 분명히 두 그룹의 평균값을 비교하기 위해 그 차이를 구하고 그 차이에서 분석을 시작했습니다. 단지 그룹이 한 개 더 늘어서 세 개가 되었는데 우리의 목적은 동일합니다. 세 집단의 평균이 같은지 다른지 알고 싶은 것이지요. 그렇다면 분석의 이름이 평균분석이어야 하지 않을까요? 갑자기 분산분석이라니 이게 무슨 뜻일까요? 뭔가 이상하지 않나요? 분산분석이라는 이름을 듣고 이사하게 생각하지 않는다면 아마도 평생 왜 이것이 분산분석인지 모르고 넘어갈 것입니다. 아마도 제가 아는 한 모든 통계수업과 통계책은 이런 설명이 없이 그냥 공식을 외우고 문제를 풀고 답을 찾게만 합니다. 왜냐고 물으면 아무도 답해주지 않습니다. 우리는 질문해야 합니다. 왜? 분산분석인가요? 평균분석이 아니고?

그럼 이제 왜 이 분석방법의 이름이 분산분석인지 알려드리겠습니다.

ANOVA 즉 분산분석의 핵심은 앞서 F-value라고 했습니다. F-value는 두 분산의 비율입니다. 그래서 우리는 이 분석을 분산분석이라고 부릅니다. 하지만 여전히 우리의 궁금증은 해결되지 않습니다. 왜냐하면 우리가 궁금한 것은 세 그룹의 평균값이 같은지 다른지 인데, 두 개의 분산으로 어떻게 세 그룹의 평균값이 같은지 다른지 알 수 있을까요? 일단 여기서 다시 분산의 공식을 떠 올려 봅시다.

\[Variance=s^2=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}\]

앞에서 해 본 것 처럼 우리가 가진 자료가 {1, 2, 3, 4, 5}라면 평균은 3이고 분산은 다음과 같이 계산될 것입니다.

\[\frac{(1-3)^2+(2-3)^2+(3-3)^2+(4-3)^2+(5-3)^2}{4}=2.5\]

앞에서 했던 분산의 계산이 기억이 나시나요? 아무것도 아닌 것 같지만 위의 계산을 잘 기억해 두시기 바랍니다. 앞으로 우리가 자주 보아야 할 것이기 때문입니다.

3.5.3 두 개의 분산

이제 예를 들어서 차근차근 알아가 봅시다.

우리가 뒤에서 실습할 예제이긴 합니다만 자주 반복해서 보다보면 더 쉽게 이해될 것입니다. 어느 인터넷 서비스 기업 (ISP: Internet Service Provider)이 자신의 고객들의 총 지불금액이 고객별 이용대금 지불방법에 따라 차이가 있는지 알고 싶다면 종속변수와 독립변수는 다음과 같습니다.

종속변수: 총 지불금액 (Total charges)
독립변수: 대금 지불방법 (총 4가지 그룹)
- 계좌이체 (Bank transfer)
- 신용카드 (Credit card)
- 전자수표 (Electronic check)
- 종이수표 (Mailed check)

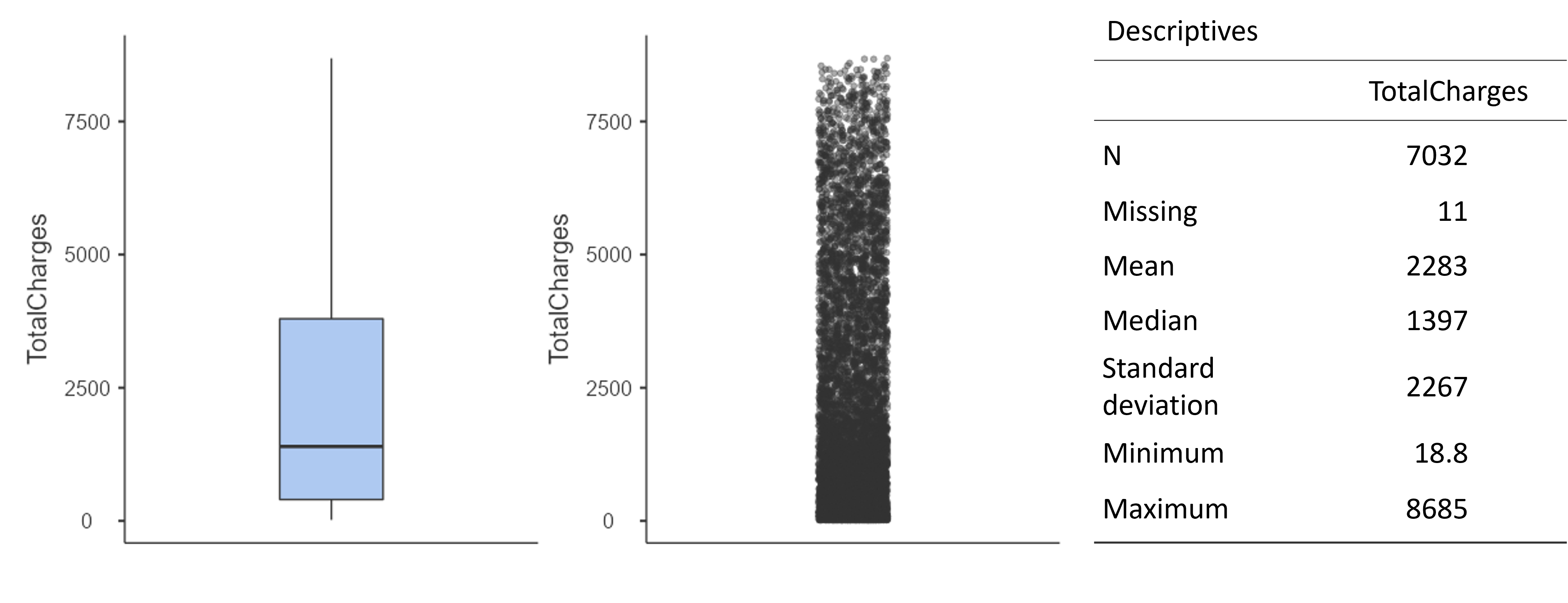
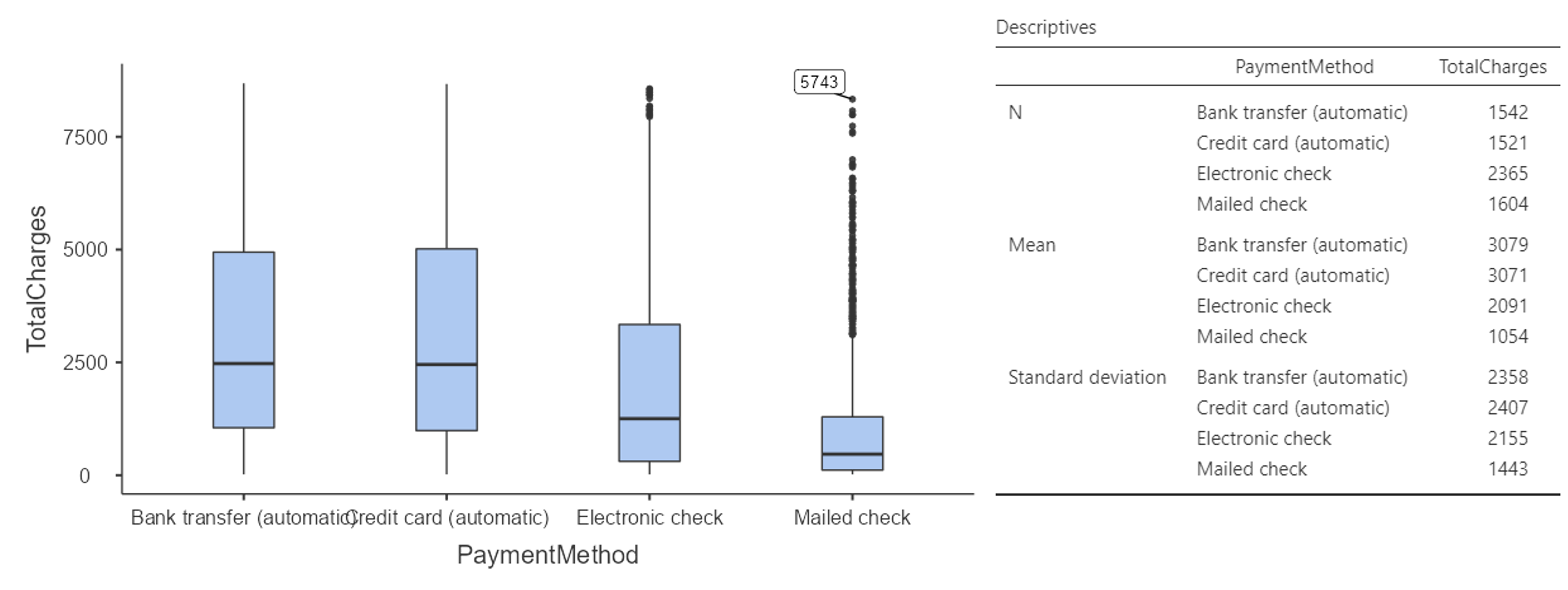
아래는 종속변수와 독립변수에 대한 기본적인 정보들입니다. 일종의 기술통계 (Descriptive statistics)라고 할 수 있습니다. 약 7000개 정도의 관측치가 있음을 알 수 있고 총 지불금액의 평균은 2,283 달러입니다. 표준편차도 2,267 달러 정도 되네요. 독립변수의 4 개의 그룹에 따른 총 지불금액의 평균은 Bank transfer와 Credit card가 약 3,000 달러 정도이고 Electronic check와 Mailed check가 각각 약 2,000 달러 수준 그리고 1,000 달러 수준임을 알 수 있습니다.

그렇다면 이제 우리는 두 개의 분산을 찾아서 F-value를 구해야 합니다. 중요한 것은 위에서 우리가 다시 계산해 보았던 분산의 공식입니다. 두 개의 분산이 존재 하려면 먼저 무엇이 두 개 필요할까요? 잠시 생각해 보시길 바랍니다.

너무 쉬운 질문이지만 의외로 답을 잘 못합니다. 두 개의 분산이 계산되려면 먼저 두 개의 평균값이 존재해야 합니다. 이제 우리는 그래프를 보면서 두 개의 평균값이 무엇인지 찾아보겠습니다. 아래의 Figure 3.14 를 확인해보기 바랍니다.

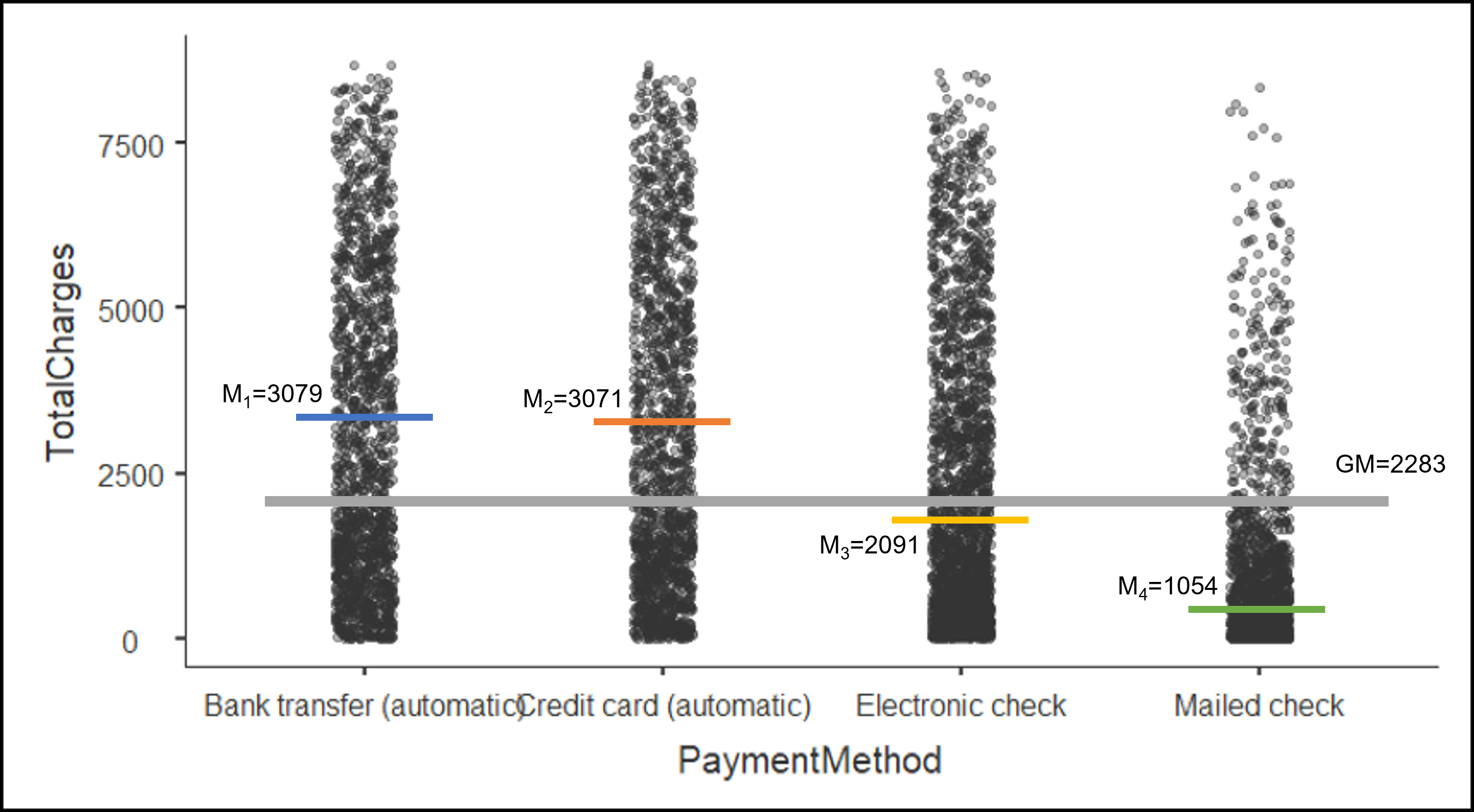
두 가지 평균값이란 바로 전체평균(GM: Grand Mean)과 그룹평균 입니다. 물론 여기서 그룹평균은 그룹이 4 개 이므로 4개의 평균값이 있지만 개념적으로 모두 같은 것이므로 하나의 그룹평균이라고 볼 수 있습니다. 현재 우리의 데이터에서 전체평균은 \(GM = 2283\) 이고 첫 번째 그룹의 평균은 \(M_1=3079\), 두 번째 그룹의 평균은 \(M_2=3071\), 세 번째 그룹의 평균은 \(M_3=2091\), 마지막으로 네 번째 그룹의 평균은 \(M_4=1054\)입니다. 그렇다면 이제 우리는 이 두 개의 평균값, 정확히는 두 가지의 평균값에서 두 개의 분산을 찾아내야 합니다. 무엇일까요?

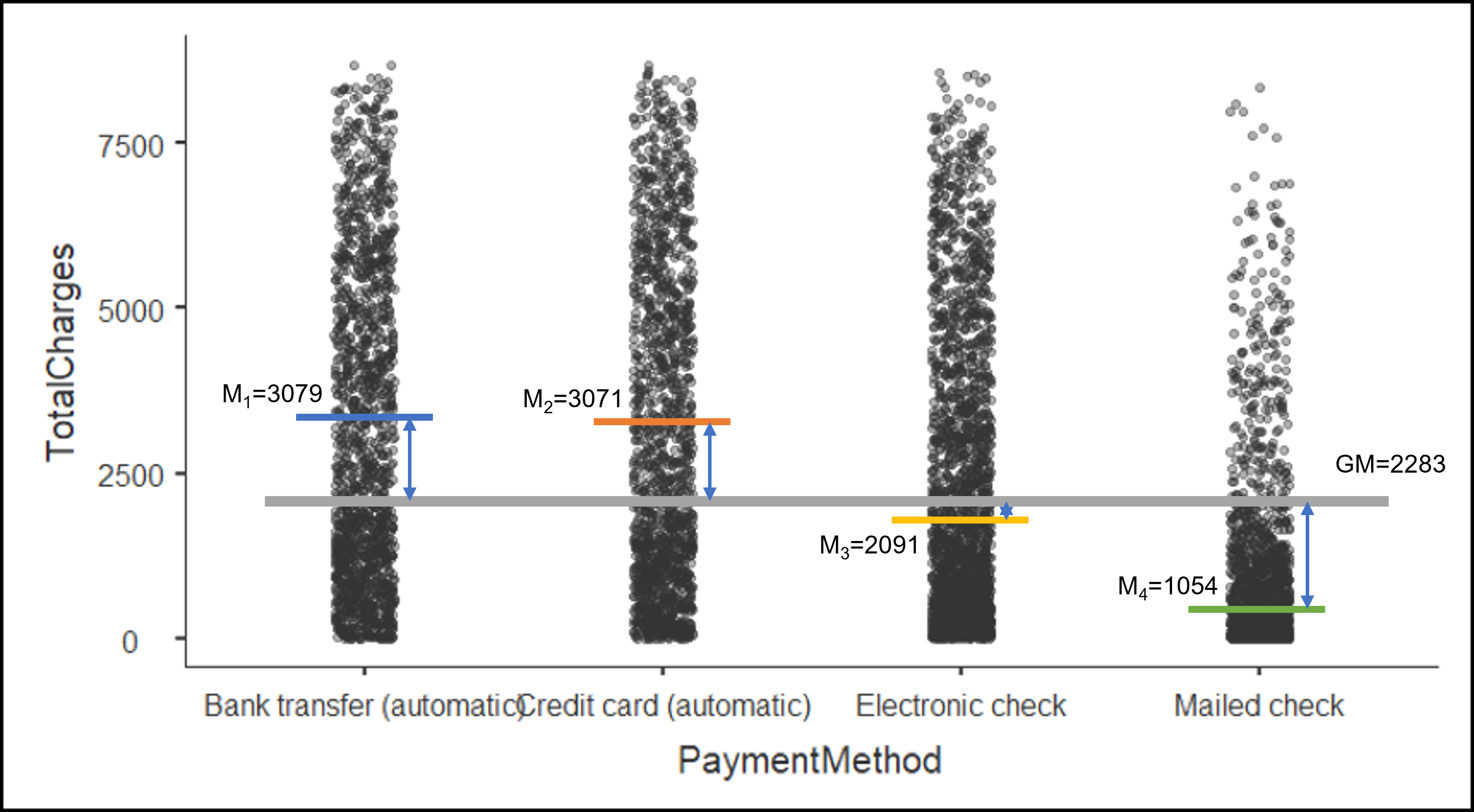
바로 그룹간 분산입니다. 이를 우리는 Between Variance라고 부릅니다. 이 Between Variance는 전체평균(GM=2283)으로부터 각 4 개의 그룹의 평균값들 사이의 거리를 의미하는 분산입니다. 위의 Figure 3.15 에서 볼 수 있듯이 말입니다. 그렇다면 이 Between Variance가 가지는 의미는 무엇일까요? 우리는 우선 이 Between Variance가 크다는 것이 어떤 의미인지를 먼저 이해해야 합니다. Between Variance가 크다는 것은 무슨 뜻일까요? 그것은 그룹의 평균값이 전체평균값에서 멀어져 있다는 것을 의미합니다. 다만, 그룹이 3 개 이상으로 여러 개이므로 우리는 정확하게 말하면, Between Variance가 크다는 것은 적어도 어떤 한 그룹의 평균값은 전체평균값으로부터 멀어져 있다고 이야기 할 수 있습니다. 이제 우리는 어떻게 분산을 이용해서 3 개 이상의 그룹의 평균값이 같은지 다른지 분석할 수 있는 단서를 알게 되었습니다. 앞의 t-test에서는 단지 두 개의 그룹이 있었기 때문에 쉽게 두 그룹의 평균값을 빼서 차이 값을 만들어 접근했다면, 그룹의 개수가 3 개 이상이 되면 이 방법이 통하지 않기 때문에 각 그룹의 평균값이 전체 평균값으로부터 얼마나 멀어져 있는지 분산을 구해서 적어도 한 그룹의 평균값은 전체평균과 다르다는 것을 찾아내는 방식이 분산분석인 것입니다. 그래서 평균분석이 아닌 분산분석이라는 이름이 되는 것이지요.

문제는 지금부터 발생합니다.

Between Variance가 크다는 것은 적어도 한 그룹의 평균값이 전체평균값에서 멀어져 있다는 의미는 알겠는데, 도대체 이 Between Variance가 얼마나 커야 큰 거신지 혹은 얼마나 작아야 작은 것인지 우리가 알 수 있을까요? 통계적으로 이 Between Variance가 충분히 크려면 얼마나 커야 할까요? 혹은 이 Between Variance가 우연히 클 확률은 얼마나 될까요?

맞습니다. 이 Between Variance 하나로는 이러한 질문에 아무런 답도 할 수 없습니다. 그런데 우리는 이런 상황을 앞에서 한 번 겪어 봤습니다. 어디에서 였을까요? 바로 t-value에서 였습니다. 다시 생각해보면 t-value의 분자부분인 두 그룹의 평균값의 차이가 우리의 관심사였습니다. 문제는 이 차이가 얼마나 커야 통계적으로 큰지 얼마나 작아야 작은지 알 수 없었다는 점입니다. 그래서 우리는 비교대상을 가져와서 나누었습니다. 즉 비율을 만든 것이지요. 지금 우리가 공부하는 F-value도 마찬가지입니다. 우리의 관심사는 Between Variance 입니다. 이 Between Variance가 커야 적어도 한 그룹의 평균값이 전체평균으로부터 멀어져 있다고 결론 내릴 수 있기 때문입니다. 문제는 이 Between Variance가 얼마나 커야 큰지 알 수 없으므로 우리는 역시 비교대상을 가져와야 합니다. 그 비교대상이 당연히 두 분산 중 나머지 한 개의 분산이 되겠죠. 그럼 비교대상이 될 나머지 한 개의 분산에 대해 알아봅시다.

위의 Figure 3.16 에서 보듯이 나머지 한 개의 분산은 그룹내 분산입니다. Within Variance라고 합니다. 이 Within Variance는 무엇이고 어떤 의미일까요? 간단하게 말하자면 앞에서 공부한 t-value의 분모의 표준편차와 동일한 의미이고 같은 역할을 합니다. 앞서 t-value에서 두 평균값의 차이가 얼마나 커야 큰지 혹은 얼마나 작아야 작은지 알 수 없기 때문에 비교대상으로 표준편차를 가져와서 비교한다는 이야기를 했습니다. 표준편차는 데이터가 평균값으로부터 멀어져 있는 평균적인 거리라고 이야기 했죠. 이 편차는 의미 없는 편차라고도 이야기 했습니다. 이 편차는 단순히 random한 편차로서 아무런 의미가 없는 편차라는 것입니다. 그래서 이런 의미 없는 편차보다도 평균값의 차이(이것도 일종의 편차이지요)가 작거나 비슷하다면 이 두 평균값의 차이는 의미 없는 차이라고 보고 유의하지 않다고 판단하고 만약 이 의미 없는 편차(표준편차)보다 확실히 크다면 두 평균값의 차이는 유의하고 뭔가 이러한 차이에는 이유가 있을 것이라는 설명을 했습니다. 이 논리는 분산분석에서도 동일합니다.

앞에서 본 Between Variance는 우리의 관심사이지만 얼마나 커야 큰지 혹은 얼마나 작아야 작은지 알 수 없습니다. 그래서 비교대상이 필요하고 우리는 비교대상으로 Within Variance를 가져온 것입니다. 이 Within Variance는 그룹내 분산으로 각 그룹내에서 데이터가 그룹의 평균값을 중심으로 퍼져 있는 평균적인 거리입니다. 즉, 의미 없는 퍼짐인 것입니다. 이러한 퍼져 있는 정도는 단순히 random한 분산일 뿐 뭔가 의미가 있지 않습니다. 따라서 Between Variance가 Within Variance보다 충분히 크지 않다면 우리는 Between Variance가 충분히 크다고 판단할 수 없을 것이므로 어떤 그룹의 평균값도 전체평균에서 그다지 멀리 떨어져 있다고 판단하기 어려울 것입니다. 따라서 모든 그룹의 평균값은 비슷하다고 결론 내려야 할 것입니다.

3.5.4 F-value

\[F-value = \frac{Between \; Variance}{Within \; Variance} = \frac{MS_{Between}}{MS_{Within}} = \frac{MS_{Treatment}}{MS_{Error}}\]

책 마다 표기 방법이 다를 수 있어 여러 가지를 써 보았습니다. 위의 식에서 핵심은 결국 F-value는 Between Variance와 Within Variance의 비율이라는 것입니다. 뒤에 나오는 \(MS_{Between}\)에 대해서 설명하자면 여기서 \(MS\)는 Mean Squared의 약자로서 분산을 의미합니다. 왜 Mean Squared라고 하냐면 기본적으로 분산의 공식을 보면 분산의 분자부분은 제곱의 합입니다. 이를 영어로 Sum of Squared라고 하는데 그냥 SS라고 부릅니다. 이것을 \(n-1\)로 나누면 분산이 되는데 사실 \(n\)으로 나누냐 혹은 \(n-1\)로 나누냐는 모집단이냐 샘플이냐의 차이일 뿐 그 의미는 데이터의 개수로 나누는 것을 의미합니다. 이는 평균값을 구할 때 데이터의 합을 데이터의 개수로 나누는 것이 평균이기 때문에, 분산에서 데이터의 개수로 나누는 것은 평균의 의미를 가지게 됩니다. 그래서 분산이나 표준편차가 평균값을 중심으로 데이터가 평균적으로 퍼져있는 거리가 되는 것이지요. 그런 의미에서 SS를 데이터의 개수로 나누었으니 이게 일종의 평균의 개념이 된다는 의미로 MS라는 말을 사용합니다. 그냥 분산이라는 의미이죠. 되게 어렵게 써 놓았으나 결론은 분산이라는 의미입니다. 다만, 어떤 책은 Between 대신에 Treatment라는 말을 사용하는데, 이는 실험연구에서 각 그룹별로 다른 처방을 내리는 것을 Treatment라고 해서 그룹별로 다르다는 것을 이런 식으로 표현한 것입니다. 또한 Within 대신에 Error를 쓰기도 하는데 여기서 Error는 무슨 문제가 있다는 의미가 아닌 단순히 random한 편차/차이라는 의미 입니다. 따라서 너무 어렵게 생각하지 말기 바랍니다.

핵심은 F-value란 두 분산인 Between Variance와 Within Variance의 비율이며 여기서 Between Variance가 크다는 것은 적어도 어느 한 그룹의 평균값이 전체평균으로부터 멀어져 있다는 의미이며, 이 크기가 얼마나 커야 큰지 혹은 얼마나 작아야 작은지 알 수 없으므로 우리는 비교대상인 Within Variance를 가져와서 비교한다는 것입니다. 여기서 Within Variance는 의미 없는 random한 분산이므로 이러한 의미 없는 분산보다 Between Variance가 충분히 커야 적어도 한 그룹의 평균값이 전체 평균값과는 다르다고 결론 내릴 수 있다는 것입니다.

축하드립니다.

이제 여러분은 분산분석의 가장 중요한 부분을 끝내셨습니다. 조금만 더 나아가 봅시다.

YouTube 바로 가기

3.6 F-value를 계산해 보자

3.6.1 통계적 가설

앞서 우리는 F-value란 Between Variance와 Within Variance의 비율이라는 것을 알았습니다. 특히 여기서 우리의 관심사는 Between Variance 였습니다. 왜냐하면 만약 Between Variance가 작다면 이것은 모든 그룹의 평균값이 전체평균과 비슷하다는 의미이고, Between Variance가 크다면 이것은 적어도 한 그룹의 평균값이 전체평균으로부터 멀어져 있으므로 다르다는 의미가 되기 때문입니다. 이제 이 말을 통계적 가설로 바꿔 보겠습니다.

\[ H_0: \mu_1 = \mu_2 = \; ... \; = \mu_k \; (k는 그룹의 갯수)\] \[ H_a: \mu_i \neq \mu_j \; for \; some \; i, j\]

위의 대립가설을 우리말로 바꾸면 적어도 한 그룹의 평균값은 다르다는 의미가 됩니다. 영어로는 대략 All means are NOT equal 정도가 되겠습니다. 왜 그런지는 사실 우리가 이미 여러 차례 이야기 했습니다. Between Variance가 통계적으로 유의하다는 것은 이 값이 Within Variance보다 충분히 크다는 것이고, 이것이 의미 하는 바는 누군지는 몰라도 적어도 한 개의 그룹의 평균값이 전체평균과 다르다는 것입니다. 물론, 한 개가 아닐 수도 있습니다. 두 개 일수도 있고 모든 그룹의 평균값이 다 다를 수도 있지만, 중요한 것은 이 정보만으로는 정확하고 자세한 내용을 알 수 없다는 점이지요. 따라서 F-value가 유의 하다는 것은 위의 통계적 가설에서 대립가설을 채택한다는 것이므로 의미상 적어도 한 그룹은 다르다 정도로만 해석이 가능한 것입니다.

3.6.2 F-value의 계산

우리가 이미 계속 반복하고 있지만 다시 한 번 분산의 계산 방법을 떠 올려 봅시다.

\[Variance=s^2=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}\]

우리가 가진 자료가 {1, 2, 3, 4, 5}라면 평균은 3이고 분산은 다음과 같이 계산될 것입니다.

\[\frac{(1-3)^2+(2-3)^2+(3-3)^2+(4-3)^2+(5-3)^2}{4}=2.5\]

이제 손으로 계산하기 쉬운 예를 하나 가지고 직접 F-value를 계산해 봅시다.

감기약의 효과를 측정하기 위해 감기약 A와 B 그리고 플라시보를 준비했습니다. 총 10명의 대상자를 세 그룹으로 나누어 감기가 낫는데까지 걸리 날자를 세어 보았습니다. 다음은 그 결과를 정리한 데이터 입니다.

Table 3.1: 예제 데이터
id	days	group
1	5.3	1
2	6.0	1
3	6.7	1
4	5.5	2
5	6.2	2
6	6.4	2
7	5.7	2
8	7.5	3
9	7.2	3
10	7.9	3

이제 우리는 Table 3.1 를 이용해서 계산을 해 보겠습니다. 먼저 그룹 평균값과 전체평균값을 구해보겠습니다.

Table 3.2: 평균값 추가
id	days	group	group mean	grand mean
1	5.3	1	6.00	6.44
2	6.0	1	6.00	6.44
3	6.7	1	6.00	6.44
4	5.5	2	5.95	6.44
5	6.2	2	5.95	6.44
6	6.4	2	5.95	6.44
7	5.7	2	5.95	6.44
8	7.5	3	7.53	6.44
9	7.2	3	7.53	6.44
10	7.9	3	7.53	6.44

Table 3.3: \(SS_{Between}\) 계산
id	days	group	group mean	grand mean	\(SS_{Between}\)
1	5.3	1	6.00	6.44	\(=(6.00-6.44)^2 = 0.194\)
2	6.0	1	6.00	6.44	\(=(6.00-6.44)^2 = 0.194\)
3	6.7	1	6.00	6.44	\(=(6.00-6.44)^2 = 0.194\)
4	5.5	2	5.95	6.44	\(=(5.95-6.44)^2 = 0.240\)
5	6.2	2	5.95	6.44	\(=(5.95-6.44)^2 = 0.240\)
6	6.4	2	5.95	6.44	\(=(5.95-6.44)^2 = 0.240\)
7	5.7	2	5.95	6.44	\(=(5.95-6.44)^2 = 0.240\)
8	7.5	3	7.53	6.44	\(=(7.53-6.44)^2 = 1.195\)
9	7.2	3	7.53	6.44	\(=(7.53-6.44)^2 = 1.195\)
10	7.9	3	7.53	6.44	\(=(7.53-6.44)^2 = 1.195\)

Table 3.3 은 Between Variance의 분자부분 즉 Sum of Squared 부분을 먼저 계산하는 것을 보여줍니다. 위에서 보듯이 1 번 그룹(감기약 A)에 3 명, 2 번 그룹(감기약 B)에 4 명, 그리고 마지막으로 3 번 그룹(플라시보)에 3명이 있어 동일한 계산을 3 회, 4 회, 3 회 반복합니다. 가끔 왜 반복하느냐고 묻는 분들이 있는데요. 간단합니다. 우리가 가진 데이터의 개수대로 해야만 정확하기 때문입니다. 예를 들어 위의 {1, 2, 3, 4, 5}라는 데이터의 분산을 구할 때도, 모든 데이터에서 전부 한 번씩 평균을 빼서 제곱을 한 뒤에 합쳐야 하는 것과 마찬가지 입니다. 첫 번째 그룹에 세 명의 사람이 있고 이 세 명의 회복일 수 의 평균이 6.00일이므로 이 6.00일이라는 평균값은 한 개가 아닌 세 개로부터 나왔으므로 세 번 전체평균과의 차이를 구해 제곱해서 합해야 합니다. 그러므로 위의 세 그룹의 경우를 단순하게 계산해 본다면 \(3 \times (6.00-6.44)^2 + 4 \times (5.95-6.44)^2 + 3 \times (7.53-6.44)^2 = 5.127\)이 됩니다. 가능하다면 엑셀에서 위의 데이터를 넣고 직접 계산해 보길 바랍니다. 직접 손으로 해보는 것과 그냥 눈으로 보는 것은 차이가 큽니다.

여기서 계산된 \(3 \times (6.00-6.44)^2 + 4 \times (5.95-6.44)^2 + 3 \times (7.53-6.44)^2 = 5.127\)은 Between Variance의 분자부분입니다. 이제 정확한 Between Variance를 계산하기 위해서는 분모부분이 필요합니다. 이 계산에서 분모부분이 바로 분산분석의 자유도 (degree of freedom)입니다. 두 개의 분산 중 이 Between Variance의 자유도가 첫 번째 자유도 입니다. \(df_1\)이라고 표기합니다. 이 자유도의 계산은 다음과 같습니다.

\[df_1 = k -1 \; (\text{k는 그룹의 갯수})\]

우리의 독립변수는 감기약 A, B 그리고 플라시보로 이루어져 있으므로 \(k = 3\)입니다. 따라서 \(df_1 = k -1 = 2\)가 됩니다. 그러므로 우리가 원하는 Between Variance는 \(SS_{Between} \div df_1 = 5.127 \div 2\)가 될 것입니다. 다음은 Within Variance를 계산해 봅시다.

Table 3.4: \(SS_{Within}\) 계산
id	days	group	group mean	\(SS_{Within}\)
1	5.3	1	6.00	\(=(5.30-6.00)^2 = 0.49\)
2	6.0	1	6.00	\(=(6.00-6.00)^2 = 0.00\)
3	6.7	1	6.00	\(=(6.70-6.00)^2 = 0.49\)
4	5.5	2	5.95	\(=(5.50-5.95)^2 = 0.20\)
5	6.2	2	5.95	\(=(6.20-5.95)^2 = 0.06\)
6	6.4	2	5.95	\(=(6.40-5.95)^2 = 0.20\)
7	5.7	2	5.95	\(=(5.70-5.95)^2 = 0.06\)
8	7.5	3	7.53	\(=(7.50-7.53)^2 = 0.001\)
9	7.2	3	7.53	\(=(7.20-7.53)^2 = 0.11\)
10	7.9	3	7.53	\(=(7.90-7.53)^2 = 0.14\)

Table 3.4 에서 보는 바와 같이, Within Variance는 각 값에서 그룹 평균값을 빼서 제곱하여 모두 합하면 됩니다. 소수점 둘째자리 이하는 절삭하였습니다. 전부 다 합쳐서 보면 약 1.757이 됩니다. 즉, \(SS_{Within} = 1.757\)이 됩니다. 이제 Within Variance의 분모부분을 알아야 합니다. 이것도 또한 자유도이며 이제 두 번째 자유도가 됩니다. \(df_2 = n - k\)입니다. 즉, 데이터의 개수에서 독립변수의 그룹의 개수를 빼주면 됩니다. 총 데이터의 개수는 10개이고 그룹은 3 개 이므로 \(df_2 = 10 - 3 = 7\)이 됩니다. 재미있는 것은 \(df_1 + df_2 = 2 + 7 = 9 = n -1\)라는 사실입니다. 두 개의 자유도를 합치니 t-test의 자유도와 동일해집니다. 자, 그런 이제 계산된 모든 값들을 정리해 봅시다.

\[F-value = \frac{Between \; Variance}{Within \; Variance} = \frac{MS_{Between}}{MS_{Within}} = \frac{MS_{Treatment}}{MS_{Error}} = \frac{\frac{5.127}{2}}{\frac{1.757}{7}} = 10.216\]

이렇게 됩니다. 결국 우리의 F-value는 약 10.216정도가 됩니다. 어떤가요? 이제 F-value가 보이시나요?

3.6.3 통계 프로그램 결과표

그런데, 보통 ANOVA를 통계 프로그램에서 돌리고 나면 아래와 같은 결과 표가 나타납니다.

Table 3.5: 분산분석 결과표
ANOVA Result
Source of variance	SS	df	MS	F-value	p-value
Between	5.127	2	2.564	10.216	0.008
Within	1.757	7	0.251
Total	6.884	9

Table 3.5 가 이해가 되시나요? 우리가 위에서 계산한 그대로 모든 숫자가 나타나 있습니다. 가장 첫 번째에 SS (Sum of Squared)가 있고 그 다음에 df 그리고 SS를 df로 나눈 MS(Mean Squared)가 나옵니다. 이 MS가 우리가 앞에서 설명했듯이 바로 분산입니다. 그리고 Between Variance를 Within Variance로 나눈 것이 바로 F-value입니다. 마지막에 p-value가 나오는데요. 5%보다 확실히 작으므로 유의합니다. 여기서 엑셀에서 저 p-value를 구할 수 있는 간단한 함수를 하나 알려드린다면 바로 fdist라는 엑셀 함수입니다. =fdist(F-value, df1, df2) 이런 순서로 넣으시면 우리가 원하는 p-value를 구할 수 있습니다.

이제 우리는 분산분석을 거의 정복했습니다. 마무리만 남았네요. 조금만 힘냅시다. 파이팅!!

YouTube 바로 가기

3.7 ANOVA의 F-table과 사후검정

3.7.1 F-table

앞서 보았던 분산분석의 결과표 Table 3.5 를 보면 p-value는 0.008로 우리가 생각하는 유의수준 \(\alpha\) 5%보다 훨씬 작아 유의합니다. 그렇다면 이 F-vlaue가 유의하다는 것은 무슨 뜻인가요? 이미 설명 했듯이 적어도 어느 한 그룹은 다르다는 정도입니다. 즉, 우리는 뭔가 더 자세한 결과를 알고 싶지만 이 상태만으로는 알 수가 없습니다. 따라서 항상 분산분석이 유의한 결과를 나타내었다면 자동적으로 사후검정 (Post-hoc test)를 해야 합니다.

사후검정을 하기 전에 먼저 F-table을 한번 보도록 하겠습니다.

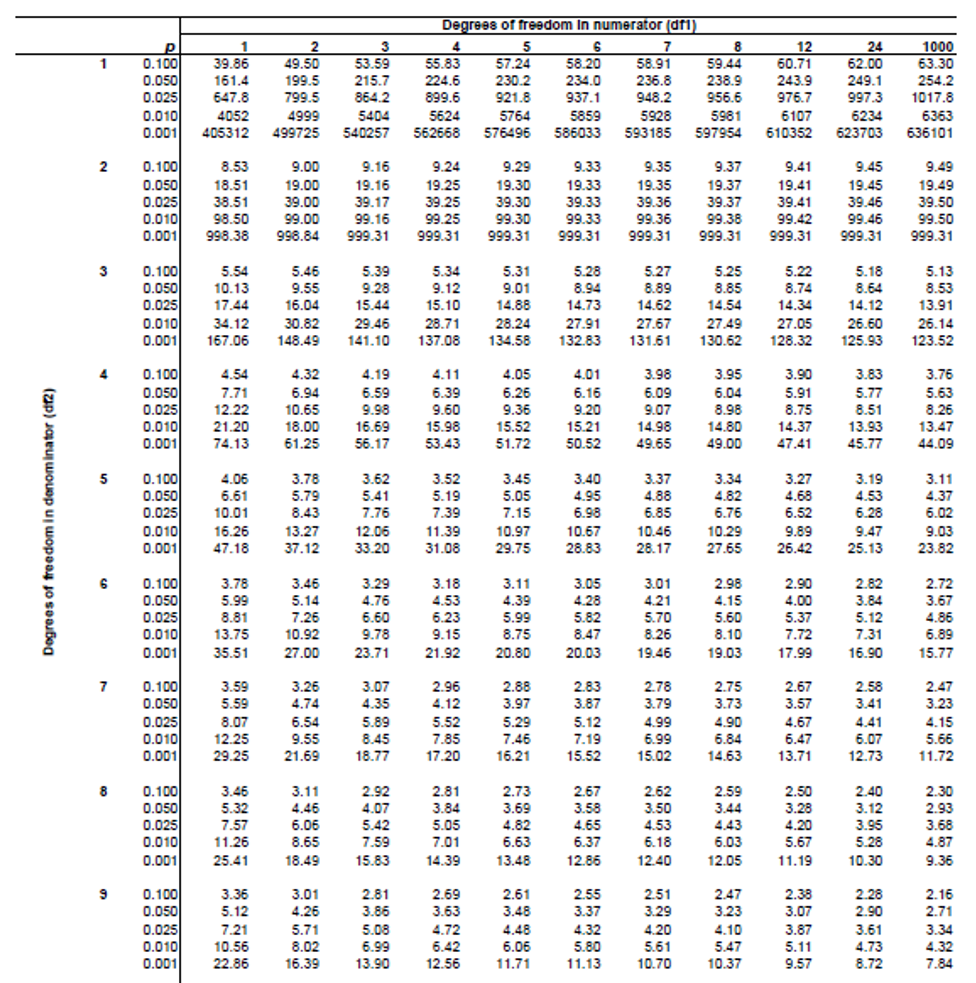
앞에서 보았던 t-table과도 조금 다릅니다. 왜냐하면 자유도가 2 개이기 때문에 \(df_1\)을 가로축에 \(df_2\)를 세로축에 둔 모양이기 때문입니다. 그럼 이제 우리가 앞에서 계산한 F-value를 가지고 F-table을 이용해 p-value를 찾아보겠습니다. 우리의 F-value는 10.216이었고, \(df_1 = 2, \; df_2 = 7\)이었습니다.

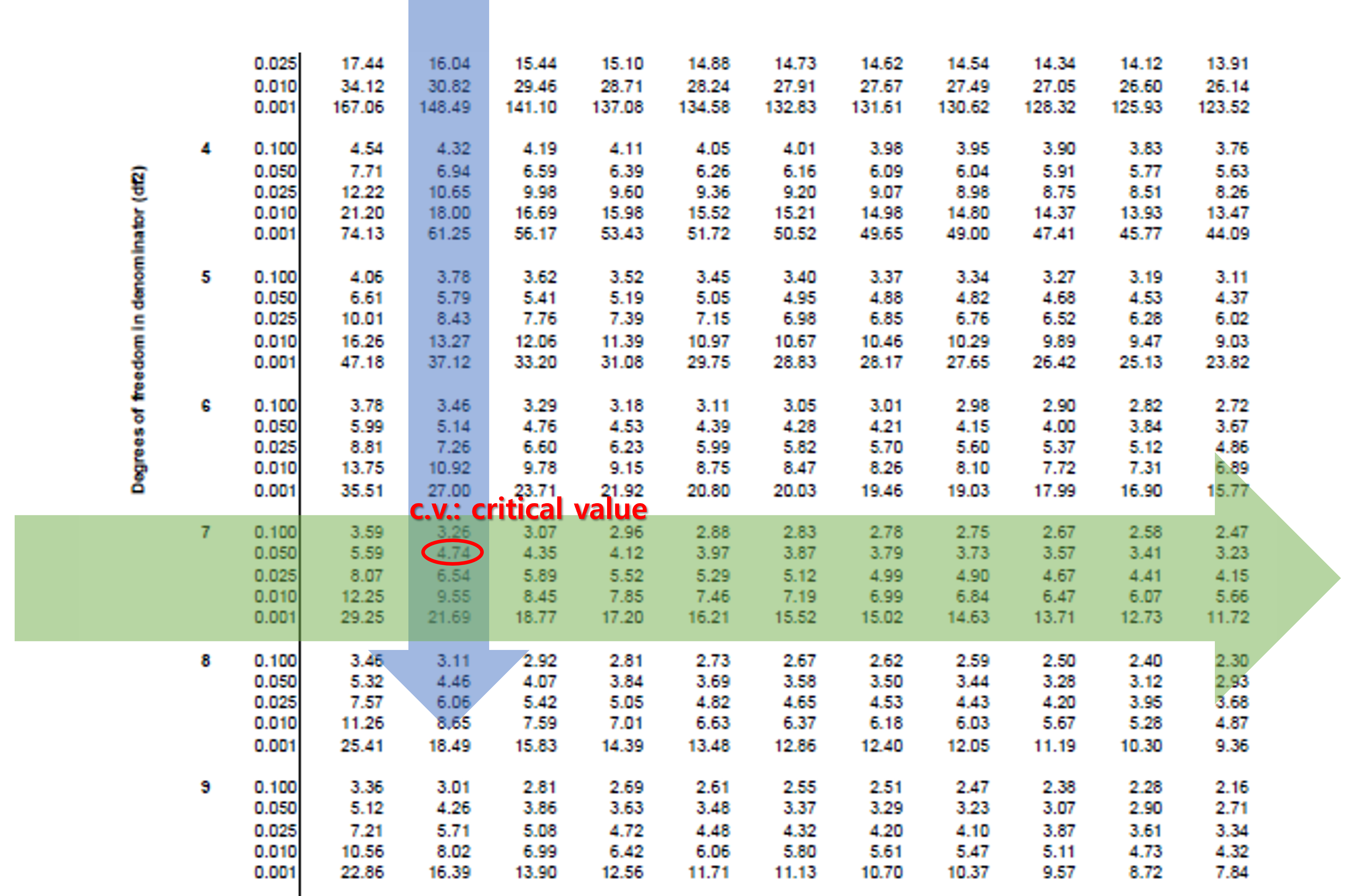
Figure 3.18 에서 우리는 두 번째 열(파란색)이 \(df_1 = 2\)이므로 쭉 따라서 내려오다가 좌측에 \(df_2 = 7\)인 초록색과 만나는 부분이 우리가 찾아야 할 부분입니다. 좌측에 보면 7이라는 숫자 우측에 소수점들이 있는데 이 부분이 바로 p-value 입니다. 우리의 유의수준은 \(\alpha = 0.05\)이므로 그 중에 두 번째 줄을 보면 4.74라는 숫자가 있습니다. 이 숫자가 바로 \(df_1 = 2, \; df_2 = 7\)인 경우 유의수준 \(\alpha = 0.05\)에 해당하는 c.v. (critical value)입니다. 앞의 t-table과 똑같이 우리의 F-value가 이 c.v. 보다 크면 유의수준 5%보다 p-value가 작아진다는 의미입니다. 우리의 F-value는 10.216이므로 c.v. 4.74보다 훨씬 큽니다. 따라서 우리의 F-value는 유의합니다. 앞에서 설명한 것처럼 보다 정확한 p-value를 알고 싶다면 엑셀의 fdist 함수를 이용하시기 바랍니다.

3.7.2 사후검정

이제 다시 유의한 분산분석의 결과로 돌아와 봅시다.

이야기 했듯이 F-value가 유의하다는 것은 적어도 한 그룹이 다르다는 것이지 그 이상도 그 이하도 아닙니다. 그러므로 보다 자세한 결과를 알고 싶다면 사후검정을 해야 합니다. 사후검정을 통해 어떤 그룹이 어떻게 다른 그룹과 같은지 다른지 알 수 있기 때문입니다. 따라서 ANOVA가 유의했다면 자동으로 사후검정을 하는 것을 습관화해야 합니다.

사후검정이란 일종의 여러 다발의 t-test입니다. 여기서 주의할 점은 사실 방법상으로는 multiple t-test와 유사하기 때문입니다. 사후검정은 multiple t-test에서 발생할 수 있는 1종오류를 제거하도록 설계된 특수한 t-test라고 볼 수 있습니다. 그러므로 사후검정을 통해 각 그룹을 1대 1로 비교 가능합니다. 이쯤 되면 누군가는 이런 생각을 할 수도 있습니다. 그렇다면 분산분석을 하지 않고 바로 사후검정을 하면 되지 않겠냐고 하는 분도 있을 수 있습니다. 그러나 이건 일종의 논리적인 프로세스입니다. 분산분석이 유의해야 사후검정이 의미가 있는 것이지 무턱대고 사후검정부터 하면 사실 좀 논리적인 문제가 발생한다고 볼 수 있습니다. 하지만, 제 개인적인 생각으로는 앞으로 어쩌면 분산분석 없이 사후검정을 하는 분석가들도 꽤 나타날 것이라는 생각이 듭니다. 왜냐하면 이게 뭔가 좀 더 직관적으로 보일 수도 있기 때문이죠. 하지만 우리는 그래도 좀 논리적인 순서대로 가봅시다. 더불어 사후검정에는 여러 가지 방법이 있습니다. 대부분 이 방법은 만든 사람 이름인데요. Fisher’s LSD / Bonferroni / Sheffe / Turkey / Duncan 등이 나름 가장 유명한 방법입니다. 이중 무엇을 써야 하느냐고 물으실 수도 있는데, 두세 가지 정도를 써보면 대부분의 경우 같은 결과가 나옵니다. 그러니 무엇이 더 좋으냐 혹은 맞느냐의 문제는 그다지 중요하지 않습니다.

다음 시간에 Jamovi를 이용해 분산분석을 직접 실습해 볼 것인데요. 여기서는 위의 데이터를 Jamovi에 넣어서 사후검정한 결과를 보여드리겠습니다.

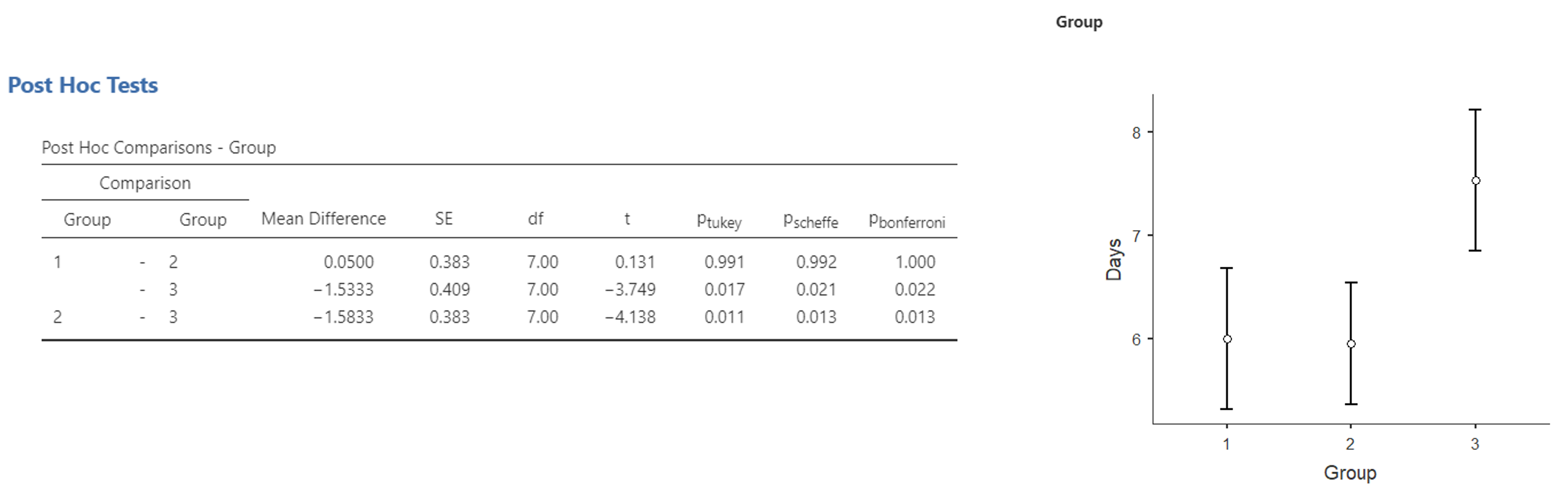
먼저 좌측의 표를 보시면 그룹 대 그룹으로 비교하는 것이 있습니다. 그룹이 1/2/3으로 되어 있습니다. 첫 번째 줄은 그룹 1과 2를 비교 한 것으로 이는 감기약 A와 B를 비교한 것인데, Tukey/Scheffe/Bonferroni 모두 유의하지 않은 결과를 보입니다. 즉, 두 감기약은 효과의 차이가 없다는 의미가 됩니다. 그러나 두 번째 줄과 세 번째 줄은 감기약 A와 플라시보를 그리고 감기약 B와 플라시보를 비교한 것인데 모두 유의합니다. 즉, 감기약 A와 B는 플라시보(위약)과 효과가 유의하게 다르다는 것입니다. 문제는 여기까지 봐도 약간 헷갈립니다. 그래서 더 좋다는 것인가 나쁘다는 것인가? 그렇습니다. 이러한 유의성만으로는 보다 정밀한 설명이 어렵습니다. 그래서 분산분석에서는 유의하면 바로 사후검정을 하고 그 사후검정 결과를 그래프로 그리는 것이 좋습니다. 가끔 이런 그래프를 안 그리는 경우가 있는데 솔직히 매우 아마추어적인 실수라고 할 수 있습니다. 분산분석에서 유의하면 사후검정과 그래프를 필수입니다. 우측의 그래프를 보면 앞의 사후검정 결과가 충분히 이해가 됩니다. 동그라미는 평균 회복일수를 그리고 평균값을 중심으로 위 아래로 뻗은 직선은 95% 유의구간입니다. 이 구간이 겹친다는 것은 기본적으로 두 그룹이 차이가 없다는 것이고 이 구간이 겹치지 않는 것은 두 그룹이 차이가 있다는 의미가 됩니다. 그림에서 보듯이 플라시보 그룹만이 확실하게 위쪽에 위치하고 있는 것이 보입니다. 그러므로 두 감기약은 플라시보 보다는 효과가 빠르지만 둘 사이에는 아무런 차이가 없다고 결론 내릴 수 있습니다.

이제 우리는 일원배치 분산분석 (One-way ANOVA)를 모두 마스터 했습니다.

여러분 수고하셨습니다. 통알못의 기초통계 1권은 여기까지입니다. 이정도 공부하셨다면 이제 통계의 아주 기초적인 분석은 마스터 하신 겁니다. 이후부터는 보다 어려운 내용이 준비되어 있습니다. 하지만 제가 여태 그래왔듯 보다 쉽게 이해하실 수 있도록 설명하겠습니다.

고생 많으셨습니다. 실습으로 넘어가 보겠습니다.

YouTube 바로 가기

3.8 ANOVA를 실습해 보자

3.8.1 실습 데이터

우리가 사용할 실습 데이터는 다음의 링크에 있습니다.

실습 데이터

이 데이터는 유투브 강의에서 설명했듯이 Kaggle.com에서 다운로드 한 것입니다. Kaggle.com에 직접 가서 다운로드 하시는 것도 방법입니다. Kaggle.com에 가시면 이 데이터의 변수들에 대한 보다 자세한 정보를 얻으실 수 있습니다.

YouTube 바로 가기